Разложение в ряд тейлора.

Как вставить математические формулы на сайт?

Если нужно когда-никогда добавлять одну-две математические формулы на веб-страницу, то проще всего сделать это, как описано в статье : математические формулы легко вставляются на сайт в виде картинок, которые автоматически генерирует Вольфрам Альфа. Кроме простоты, этот универсальный способ поможет улучшить видимость сайта в поисковых системах. Он работает давно (и, думаю, будет работать вечно), но морально уже устарел.

Если же вы постоянно используете математические формулы на своем сайте, то я рекомендую вам использовать MathJax - специальную библиотеку JavaScript, которая отображает математические обозначения в веб-браузерах с использованием разметки MathML, LaTeX или ASCIIMathML.

Есть два способа, как начать использовать MathJax: (1) при помощи простого кода можно быстро подключить к вашему сайту скрипт MathJax, который будет в нужный момент автоматически подгружаться с удаленного сервера (список серверов ); (2) закачать скрипт MathJax с удаленного сервера на свой сервер и подключить ко всем страницам своего сайта. Второй способ - более более сложный и долгий - позволит ускорить загрузку страниц вашего сайта, и если родительский сервер MathJax по каким-то причинам станет временно недоступен, это никак не повлияет на ваш собственный сайт. Несмотря на эти преимущества, я выбрал первый способ, как более простой, быстрый и не требующий технических навыков. Следуйте моему примеру, и уже через 5 минут вы сможете использовать все возможности MathJax на своем сайте.

Подключить скрипт библиотеки MathJax с удаленного сервера можно при помощи двух вариантов кода, взятого на главном сайте MathJax или же на странице документации :

Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами и или же сразу после тега . По первому варианту MathJax подгружается быстрее и меньше тормозит страницу. Зато второй вариант автоматически отслеживает и подгружает свежие версии MathJax. Если вставить первый код, то его нужно будет периодически обновлять. Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax.

Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно). Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.

Любой фрактал строится по определенному правилу, которое последовательно применяется неограниченное количество раз. Каждый такой раз называется итерацией.

Итеративный алгоритм построения губки Менгера достаточно простой: исходный куб со стороной 1 делится плоскостями, параллельными его граням, на 27 равных кубов. Из него удаляются один центральный куб и 6 прилежащих к нему по граням кубов. Получается множество, состоящее из 20 оставшихся меньших кубов. Поступая так же с каждым из этих кубов, получим множество, состоящее уже из 400 меньших кубов. Продолжая этот процесс бесконечно, получим губку Менгера.

16.1. Разложение элементарных функций в ряды Тейлора иМаклорена

Покажем, что если произвольная функция задана на множестве
, в окрестности точки
имеет множество производных и является суммой степенного ряда:

то можно найти коэффициенты этого ряда.

Подставим в степенной ряд
. Тогда
.

Найдем первую производную функции
:

При
:
.

Для второй производной получим:

При
:
.

Продолжая эту процедуру n раз получим:
.

Таким образом, получили степенной ряд вида:

,

который называется рядом Тейлора для функции
в окресности точки
.

Частным случаем ряда Тейлора является ряд Маклорена при
:

Остаток ряда Тейлора (Маклорена) получается отбрасыванием от основных рядов n первых членов и обозначается как
. Тогда функцию
можно записать как суммуn первых членов ряда
и остатка
:,

.

Остаток обычно
выражают разными формулами.

Одна из них в форме Лагранжа:

, где
.
.

Заметим, что на практике чаще используетсяряд Маклорена. Таким образом, для того, чтобы записать функцию
в виде суммыстепенного ряданеобходимо:

1) найти коэффициенты ряда Маклорена (Тейлора);

2) найти область сходимости полученного степенногоряда;

3) доказать, что данный ряд сходитсяк функции
.

Теорема 1 (необходимое и достаточное условие сходимости ряда Маклорена). Пусть радиус сходимости ряда
. Для того, чтобы этот ряд сходился в интервале
к функции
,необходимо и достаточно, чтобы выполнялось условие:
в указанном интервале.

Теорема 2. Если производные любого порядка функции
в некотором промежутке
ограниченны по абсолютной величине одним и тем же числомM , то есть
, то в этом промежутке функцию
можно разложитьв ряд Маклорена.

Пример 1 . Разложить в ряд Тейлора вокрестноститочки
функцию.

Решение.

.

,;

,
;

,
;

,

.......................................................................................................................................

,
;

Область сходимости
.

Пример 2 . Разложить функциюв ряд Тейлора вокрестноститочки
.

Решение:

Находим значение функции и ее производных при
.

,
;

,
;

...........……………………………

,
.

Подставляем эти значения в ряд. Получаем:

или
.

Найдем область сходимости этого ряда. По признаку Даламбера ряд сходится, если

.

Следовательно, при любом этот пределменее 1, а потому область сходимости ряда будет:
.

Рассмотрим несколько примеров разложенияв ряд Маклорена основных элементарных функций. Напомним, что ряд Маклорена:

.

сходитсянаинтервале
к функции
.

Отметим, что для разложенияфункции в ряд необходимо:

а) найти коэффициенты ряда Маклорена для данной функции;

б) вычислить радиус сходимостидля полученного ряда;

в) доказать, что полученный ряд сходитсяк функции
.

Пример 3. Рассмотримфункцию
.

Решение.

Вычислим значение функции и ее производных при
.

Тогда числовые коэффициенты ряда имеют вид:

для любого n. Подставим найденные коэффициенты в ряд Маклорена и получим:

Найдем радиус сходимости полученного ряда, а именно:

.

Следовательно, ряд сходитсянаинтервале
.

Этот ряд сходитсяк функции при любых значениях , потому чтоналюбом промежутке
функция иее производныепоабсолютной величинеограничены числом .

Пример 4 . Рассмотрим функцию
.

Решение .

:

Нетрудно заметить, что производные четногопорядка
, а производные нечетногопорядка. Подставим найденные коэффициенты в ряд Маклорена иполучимразложение:

Найдем интервал сходимости данного ряда. По признаку Даламбера:

для любого . Следовательно, ряд сходитсянаинтервале
.

Этот ряд сходитсяк функции
, потому что все ее производные ограничены единицей.

Пример 5 .
.

Решение.

Найдем значение функции и ее производных при
:

Таким образом, коэффициенты данного ряда:
и
, следовательно:

Аналогично с предыдущим рядом область сходимости
. Ряд сходитсяк функции
, потому что все еепроизводные ограничены единицей.

Обратим внимание, что функция
нечетнаяи разложениев рядпо нечетнымстепеням, функция
– четная и разложение в ряд по четным степеням.

Пример 6 . Биномиальный ряд:
.

Решение .

Найдем значение функции и ее производных при
:

Отсюда видно, что:

Подставим эти значения коэффициентов в ряд Маклорена и получим разложение данной функции в степенной ряд:

Найдем радиус сходимости этого ряда:

Следовательно, ряд сходится на интервале
. В предельных точках при
и
ряд может сходится или нет в зависимости от показателя степени
.

Исследованный ряд сходится на интервале
к функции
, то есть суммаряда
при
.

Пример 7 . Разложим в ряд Маклорена функцию
.

Решение.

Для разложенияв ряд этой функции используем биномиальный ряд при
. Получим:

На основе свойства степенных рядов (степенной ряд можно интегрировать в области его сходимости) найдем интеграл от левой и правой частей данного ряда:

Найдем область сходимости данного ряда:
,

то есть областью сходимости данного ряда является интервал
. Определим сходимость ряда на концах интервала. При

. Этот ряд является гармоничным рядом, то есть расходится. При
получим числовой ряд с общим членом
.

Ряд по признаку Лейбница сходится. Таким образом, областью сходимости данного ряда является промежуток
.

16.2. Применение степенных рядов степеней в приближенных вычислениях

В приближенных вычислениях степенные ряды играют исключительно большую роль. С их помощью составлены таблицы тригонометрических функций, таблицы логарифмов, таблицы значений других функций, которые используют в разных областях знаний, например в теории вероятностей и математической статистике. Кроме того, разложениефункций в степенной ряд полезно для их теоретического исследования. Главным вопросом при использовании степенных рядов в приближенных вычислениях является вопрос оценки погрешности при замене суммы ряда суммой его первыхn членов.

Рассмотрим два случая:

функция разложена в знакочередующийся ряд;

функция разложена в знакопостоянный ряд.

Вычисление с помощью знакочередующихся рядов

Пусть функция
разложена в знакочередующийся степенной ряд. Тогда при вычислении этой функции для конкретного значения получаем числовой ряд, к которому можно применить признак Лейбница. В соответствии с этим признаком, если сумму ряда заменить суммой его первыхn членов, то абсолютная погрешность не превышает первого члена остатка этого ряда, то есть:
.

Пример 8 . Вычислить
с точностью до 0,0001.

Решение .

Будем использовать ряд Маклорена для
, подставив значение угла в радианах:

Если сравнить первый и второй члены ряда с заданной точностью, то: .

Третий член разложения:

меньше заданной точности вычисления. Следовательно, для вычисления
достаточно оставить два члена ряда, то есть

.

Таким образом
.

Пример 9 . Вычислить
с точностью 0,001.

Решение .

Будем использовать формулу биномиального ряда. Для этого запишем
в виде:
.

В этом выражении
,

Сравним каждый из членов ряда с точностью, которая задана. Видно, что
. Следовательно, для вычисления
достаточно оставить три члена ряда.

или
.

Вычисление с помощью знакоположительных рядов

Пример 10 . Вычислить число с точностью до 0,001.

Решение .

В ряд для функцїї
подставим
. Получим:

Оценим погрешность, которая возникает при замене суммы ряда суммой первых членов. Запишем очевидное неравенство:

то есть 2 0, т.е. этот ряд сходится на интервале .

Тогда каждому значению х из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначая её через f (x ), можем записать равенство

понимая его в том смысле, что сумма ряда в каждой точке х из интервала сходимости равна значению функции f (x ) в этой точке. В этом же смысле будем говорить, что степенной ряд (29) сходится к функции f (x ) на интервале сходимости.

Вне интервала сходимости равенство (30) не имеет смысла.

Пример 7. Найти сумму сумму степенного ряда

Решение. Это геометрический ряд, у которого a = 1, а q = x . Следовательно, его сумма есть функция . Ряд сходится, если , а - его интервал сходимости. Поэтому равенство

справедливо лишь для значений , хотя функция определена для всех значений х , кроме х = 1.

Можно доказать, что сумма степенного ряда f (x ) непрерывна и дифференцируема на любом отрезке внутри интервала сходимости, в частности в любой точке интервала сходимости ряда.

Приведем теоремы о почленном дифференцировании и интегрировании степенных рядов.

Теорема 1. Степенной ряд (30) в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что исходный ряд, а суммы их соответственно равны .

Теорема 2. Степенной ряд (30) можно неограниченное число раз почленно интегрировать в пределах от 0 до х , если , причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны

Разложение функций в степенные ряды

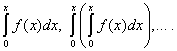
Пусть дана функция f (x ), которую требуется разложить в степенной ряд, т.е. представить в виде (30):

Задача состоит в определении коэффициентов ряда (30). Для этого, дифференцируя равенство (30) почленно, последовательно найдём:

……………………………………………….. (31)

Полагая в равенствах (30) и (31) х = 0, находим

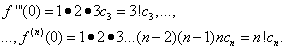
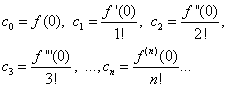
Подставляя найденные выражения в равенство (30), получим

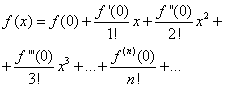(32)

Найдём разложение в ряд Маклорена некоторых элементарных функций.

Пример 8. Разложить в ряд Маклорена функцию

Решение. Производные этой функции совпадают с самой функцией:

Поэтому при х = 0 имеем

Подставляя эти значения в формулу (32), получим искомое разложение:

(33)

Этот ряд сходится на всей числовой прямой (его радиус сходимости ).

В теории функциональных рядов центральное место занимает раздел, посвященный разложению функции в ряд.

Таким образом, ставится задача: по заданной функции требуется найти такой степенной ряд

который на некотором интервале сходился и его сумма была равна
, т.е.

= ..

Эта задача называется задачей разложения функции в степенной ряд.

Необходимым условием разложимости функции в степенной ряд является её дифференцируемость бесконечное число раз – это следует из свойств сходящихся степенных рядов. Такое условие выполняется, как правило, для элементарных функций в их области определения.

Итак, предположим, что функция
имеет производные любого порядка. Можно ли её разложить в степенной ряд, если можно, то как найти этот ряд? Проще решается вторая часть задачи, с неё и начнем.

Допустим, что функцию
можно представить в виде суммы степенного ряда, сходящегося в интервале, содержащем точкух 0 :

= .. (*)

где а 0 ,а 1 ,а 2 ,...,а п ,... – неопределенные (пока) коэффициенты.

Положим в равенстве (*) значение х = х 0 , тогда получим

.

Продифференцируем степенной ряд (*) почленно

= ..

и полагая здесь х = х 0 , получим

.

При следующем дифференцировании получим ряд

= ..

полагая х = х 0 , получим
, откуда
.

После п -кратного дифференцирования получим

Полагая в последнем равенстве х = х 0 , получим
, откуда

Итак, коэффициенты найдены

,
,
, …,
,….,

подставляя которые в ряд (*), получим

Полученный ряд называется рядом Тейлора для функции
.

Таким образом, мы установили, что если функцию можно разложить в степенной ряд по степеням (х - х 0 ), то это разложение единственно и полученный ряд обязательно является рядом Тейлора.

Заметим, что ряд Тейлора можно получить для любой функции, имеющей производные любого порядка в точке х = х 0 . Но это еще не означает, что между функцией и полученным рядом можно поставить знак равенства, т.е. что сумма ряда равна исходной функции. Во-первых, такое равенство может иметь смысл только в области сходимости, а полученный для функции ряд Тейлора может и расходиться, во-вторых, если ряд Тейлора будет сходиться, то его сумма может не совпадать с исходной функцией.

3.2. Достаточные условия разложимости функции в ряд Тейлора

Сформулируем утверждение, с помощью которого будет решена поставленная задача.

Если функция
в некоторой окрестности точки х 0 имеет производные до (n + 1)-го порядка включительно, то в этой окрестности имеет место формула Тейлора

где R n (х )-остаточный член формулы Тейлора – имеет вид (форма Лагранжа)

где точка ξ лежит между х и х 0 .

Отметим, что между рядом Тейлора и формулой Тейлора имеется различие: формула Тейлора представляет собой конечную сумму, т.е. п - фиксированное число.

Напомним, что сумма ряда S (x ) может быть определена как предел функциональной последовательности частичных сумм S п (x ) на некотором промежутке Х :

.

Согласно этому, разложить функцию в ряд Тейлора означает найти такой ряд, что для любого х X

Запишем формулу Тейлора в виде, где

Заметим, что
определяет ту ошибку, которую мы получаем, заменяй функцию f (x ) многочленом S n (x ).

Если
, то
,т.е. функция разлагается в ряд Тейлора. Инаоборот, если
, то
.

Тем самыммы доказали критерий разложимости функции в ряд Тейлора.

Для того, чтобы в некотором промежутке функция f (х) разлагалась в ряд Тейлора, необходимо и достаточно, чтобы на этом промежутке
, где R n (x ) - остаточный член ряда Тейлора.

С помощью сформулированного критерия можно получить достаточные условия разложимости функции в ряд Тейлора.

Если в некоторой окрестности точки х 0 абсолютные величины всех производных функции ограничены одним и тем же числом М ≥ 0, т.е.

, т о в этой окрестности функция разлагается в ряд Тейлора.

Из вышеизложенного следует алгоритм разложения функции f (x ) в ряд Тейлора в окрестности точки х 0 :

1. Находим производные функции f (x ):

f(x), f’(x), f”(x), f’”(x), f (n) (x),…

2. Вычисляем значение функции и значения её производных в точке х 0

f(x 0 ), f’(x 0 ), f”(x 0 ), f’”(x 0 ), f (n) (x 0 ),…

3. Формально записываем ряд Тейлора и находим область сходимости полученного степенного ряда.

4. Проверяем выполнение достаточных условий, т.е. устанавливаем, для каких х из области сходимости, остаточный член R n (x ) стремится к нулю при
или
.

Разложение функций в ряд Тейлора по данному алгоритму называют разложением функции в ряд Тейлора по определению или непосредственным разложением.