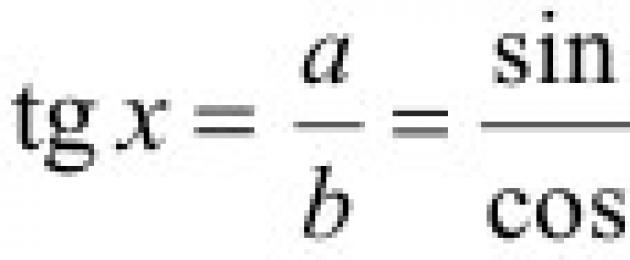Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля - до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
При выполнении тригонометрических преобразований следуйте следующим советам:
- Не пытайтесь сразу придумать схему решения примера от начала до конца.
- Не пытайтесь преобразовывать сразу весь пример. Продвигайтесь вперёд маленькими шагами.
- Помните, что кроме тригонометрических формул в тригонометрии можно по-прежнему применять все справедливые алгебраические преобразования (вынесение за скобку, сокращение дробей, формулы сокращённого умножения и так далее).
- Верьте, что всё будет хорошо.
Основные тригонометрические формулы
Большинство формул в тригонометрии часто применяется как справа налево, так и слева направо, поэтому учить эти формулы нужно так хорошо, чтобы Вы легко смогли применить некоторую формулу в обоих направлениях. Запишем для начала определения тригонометрических функций. Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
![]()
Определение котангенса:

Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
![]()
![]()
Формулы двойного угла. Синус двойного угла:

Косинус двойного угла:
Тангенс двойного угла:

Котангенс двойного угла:

Дополнительные тригонометрические формулы
Тригонометрические формулы сложения. Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:

Тангенс разности:

Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение. Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:

Разность тангенсов:

Сумма котангенсов:

Разность котангенсов:

Тригонометрические формулы преобразования произведения в сумму. Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени.
![]()
![]()
![]()
![]()
Формулы половинного угла.
![]()
![]()
Тригонометрические формулы приведения
Функцию косинус называют кофункцией функции синус и наоборот. Аналогично функции тангенс и котангенс являются кофункциями. Формулы приведения можно сформулировать в виде следующего правила:
- Если в формуле приведения угол вычитается (прибавляется) из 90 градусов или 270 градусов, то приводимая функция меняется на кофункцию;
- Если же в формуле приведения угол вычитается (прибавляется) из 180 градусов или 360 градусов, то название приводимой функции сохраняется;
- При этом перед приведенной функцией ставится тот знак, который имеет приводимая (т.е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
Формулы приведения задаются в виде таблицы:

По тригонометрической окружности легко определять табличные значения тригонометрических функций:

Тригонометрические уравнения
Для решения некоторого тригонометрического уравнения его нужно свести к одному из простейших тригонометрических уравнений, которые будут рассмотрены ниже. Для этого:
- Можно применять тригонометрические формулы приведенные выше. При этом не нужно пытаться преобразовать сразу весь пример, а нужно двигаться вперед маленькими шагами.
- Нужно не забывать о возможности преобразовать некоторое выражение и с помощью алгебраических методов, т.е. например, вынести что-нибудь за скобку или, наоборот, раскрыть скобки, сократить дробь, применить формулу сокращенного умножения , привести дроби к общему знаменателю и так далее.
- При решении тригонометрических уравнений можно применять метод группировки . При этом нужно помнить, что для того чтобы произведение нескольких множителей было равно нолю, достаточно чтобы любой из них был равен нолю, а остальные существовали .
- Применяя метод замены переменной , как обычно, уравнение после введения замены должно стать проще и не содержать первоначальной переменной. Также нужно не забыть выполнить обратную замену.
- Помните, что однородные уравнения часто встречаются и в тригонометрии.
- Раскрывая модули или решая иррациональные уравнения с тригонометрическими функциями нужно помнить и учитывать все тонкости решения соответствующих уравнений с обычными функциями.
- Помните про ОДЗ (в тригонометрических уравнениях ограничения на ОДЗ в основном сводятся к тому, что делить на ноль нельзя, но не забываем и о других ограничениях, особенно о положительности выражений в рациональных степенях и под корнями четных степеней). Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.
Главное, если не знаете, что делать, делайте хоть что-нибудь, при этом главное правильно использовать тригонометрические формулы. Если то, что Вы при этом получаете становиться все лучше и лучше, значит продолжайте решение, а если становиться хуже, значит вернитесь к началу и попробуйте применить другие формулы, так поступайте пока не наткнетесь на правильный ход решения.
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
\(\blacktriangleright\) Рассмотрим прямоугольную систему координат и в ней окружность с единичным радиусом и центром в начале координат.
Угол в \(1^\circ\) - это такой центральный угол, который опирается на дугу, длина которой равна \(\dfrac1{360}\) длины всей окружности.
\(\blacktriangleright\)
Будем рассматривать на окружности такие углы, у которых вершина находится в центре окружности, а одна сторона всегда совпадает с положительным направлением оси \(Ox\)
(на рисунке выделено красным).
На рисунке таким образом отмечены углы \(45^\circ,\ 180^\circ,\
240^\circ\)
:
Заметим, что угол \(0^\circ\) - это угол, обе стороны которого совпадают с положительным направлением оси \(Ox\) .
Точку, в которой вторая сторона такого угла \(\alpha\)
пересекает окружность, будет называть \(P_{\alpha}\)
.
Положение точки \(P_{0}\)
будем называть начальным положением.
Таким образом, можно сказать, что мы совершаем поворот по окружности из начального положения \(P_0\) до положения \(P_{\alpha}\) на угол \(\alpha\) .
\(\blacktriangleright\) Поворот по окружности против часовой стрелки - это поворот на положительный угол. Поворот по часовой стрелке - это поворот на отрицательный угол.
Например, на рисунке отмечены углы \(-45^\circ, -90^\circ, -160^\circ\) :

\(\blacktriangleright\) Рассмотрим точку \(P_{30^\circ}\) на окружности. Для того, чтобы совершить поворот по окружности из начального положения до точки \(P_{30^\circ}\) , необходимо совершить поворот на угол \(30^\circ\) (оранжевый). Если мы совершим полный оборот (то есть на \(360^\circ\) ) и еще поворот на \(30^\circ\) , то мы снова попадем в эту точку, хотя уже был совершен поворот на угол \(390^\circ=360^\circ+30^\circ\) (голубой). Также попасть в эту точку мы можем, совершив поворот на \(-330^\circ\) (зеленый), на \(750^\circ=360^\circ+360^\circ+30^\circ\) и т.д.

Таким образом, каждой точке на окружности соответствует бесконечное множество углов, причем отличаются эти углы друг от друга на целое число полных оборотов (\(n\cdot360^\circ, n\in\mathbb{Z}\)
).
Например, угол \(30^\circ\)
на \(360^\circ\)
больше, чем угол \(-330^\circ\)
, и на \(2\cdot 360^\circ\)
меньше, чем угол \(750^\circ\)
.
Все углы, находящиеся в точке \(P_{30^\circ}\)
можно записать в виде: \(\alpha=30^\circ+n\cdot 360^\circ, \ n\in\mathbb{Z}\)
.
\(\blacktriangleright\)
Угол в \(1\)
радиан
- это такой центральный угол, который опирается на дугу, длина которой равна радиусу окружности:
Т.к. длина всей окружности радиусом \(R\) равна \(2\pi R\) , а в градусной мере - \(360^\circ\) , то имеем \(360^\circ=2\pi \cdot 1\textbf{ рад}\) , откуда \ Это основная формула, с помощью которой можно переводить градусы в радианы и наоборот.
Пример 1. Найти радианную меру угла \(60^\circ\) .
Т.к. \(180^\circ = \pi \Rightarrow 1^\circ = \dfrac{\pi}{180} \Rightarrow 60^\circ=\dfrac{\pi}3\)
Пример 2. Найти градусную меру угла \(\dfrac34 \pi\) .
Т.к. \(\pi=180^\circ \Rightarrow \dfrac34 \pi=\dfrac34 \cdot 180^\circ=135^\circ\) .
Обычно пишут, например, не \(\dfrac{\pi}4 \text{ рад}\) , а просто \(\dfrac{\pi}4\) (т.е. единицу измерения “рад” опускают). Обратим внимание, что обозначение градуса при записи угла не опускают . Таким образом, под записью “угол равен \(1\) ” понимают, что “угол равен \(1\) радиану”, а не “угол равен \(1\) градусу”.
Т.к. \(\pi \thickapprox 3,14 \Rightarrow 180^\circ \thickapprox 3,14
\textbf{ рад} \Rightarrow 1 \textbf{ рад} \thickapprox 57^\circ\)
.
Такую приблизительную подстановку делать в задачах нельзя, но знание того, чему приближенно равен \(1\)
радиан в градусах часто помогает при решении некоторых задач. Например, таким образом проще найти на окружности угол в \(5\)
радиан: он примерно равен \(285^\circ\)
.
\(\blacktriangleright\)
Из курса планиметрии (геометрии на плоскости) мы знаем, что для углов \(0<\alpha< 90^\circ\)
определены синус, косинус, тангенс и котангенс следующим образом:
если дан прямоугольный треугольник со сторонами \(a, b, c\)
и углом \(\alpha\)
, то:

Т.к. на единичной окружности определены любые углы \(\alpha\in(-\infty;+\infty)\)
, то нужно определить синус, косинус, тангенс и котангенс для любого угла.
Рассмотрим единичную окружность и на ней угол \(\alpha\)
и соответствующую ему точку \(P_{\alpha}\)
:

Опустим перпендикуляр \(P_{\alpha}K\)
из точки \(P_{\alpha}\)
на ось \(Ox\)
. Мы получим прямоугольный треугольник \(\triangle OP_{\alpha}K\)
, из которого имеем: \[\sin\alpha=\dfrac{P_{\alpha}K}{P_{\alpha}O} \qquad \cos \alpha=\dfrac{OK}{P_{\alpha}O}\]
Заметим, что отрезок \(OK\)
есть не что иное, как абсцисса \(x_{\alpha}\)
точки \(P_{\alpha}\)
, а отрезок \(P_{\alpha}K\)
- ордината \(y_{\alpha}\)
. Заметим также, что т.к. мы брали единичную окружность, то \(P_{\alpha}O=1\)
- ее радиус.
Таким образом, \[\sin\alpha=y_{\alpha}, \qquad \cos \alpha=x_{\alpha}\]
Таким образом, если точка \(P_{\alpha}\) имела координаты \((x_{\alpha}\,;y_{\alpha})\) , то через соответствующий ей угол ее координаты можно переписать как \((\cos\alpha\,;\sin\alpha)\) .
Определение: 1. Синусом угла \(\alpha\) называется ордината точки \(P_{\alpha}\) , соответствующей этому углу, на единичной окружности.
2. Косинусом угла \(\alpha\) называется абсцисса точки \(P_{\alpha}\) , соответствующей этому углу, на единичной окружности.
Поэтому ось \(Oy\) называют осью синусов, ось \(Ox\) - осью косинусов.
\(\blacktriangleright\)
Окружность можно разбить на \(4\)
четверти, как показано на рисунке.
Т.к. в \(I\)
четверти и абсциссы, и ординаты всех точек положительны, то косинусы и синусы всех углов из этой четверти также положительны.
Т.к. во \(II\)
четверти ординаты всех точек положительны, а абсциссы - отрицательны, то косинусы всех углов из этой четверти - отрицательны, синусы - положительны.
Аналогично можно определить знак синуса и косинуса для оставшихся четвертей.
Пример 3. Так как, например, точки \(P_{\frac{\pi}{6}}\) и \(P_{-\frac{11\pi}6}\) совпадают, то их координаты равны, т.е. \(\sin\dfrac{\pi}6=\sin \left(-\dfrac{11\pi}6\right),\ \cos \dfrac{\pi}6=\cos \left(-\dfrac{11\pi}6\right)\) .
Пример 4. Рассмотрим точки \(P_{\alpha}\) и \(P_{\pi-\alpha}\) . Пусть для удобства \(0<\alpha<\dfrac{\pi}2\) .

Проведем перпендикуляры на ось \(Ox\)
: \(OK\)
и \(OK_1\)
. Треугольники \(OKP_{\alpha}\)
и \(OK_1P_{\pi-\alpha}\)
равны по гипотенузе и углу (\(\angle P_{\alpha}OK=\angle P_{\pi-\alpha}OK_1=\alpha\)
).
Следовательно, \(OK=OK_1, KP_{\alpha}=K_1P_{\pi-\alpha}\)
.
Т.к. координаты точки \(P_{\alpha}=(OK;KP_{\alpha})=(\cos\alpha\,;\sin\alpha)\)
, а точки \(P_{\pi-\alpha}=(-OK_1;K_1P_{\pi-\alpha})=(\cos(\pi-\alpha)\,;\sin(\pi-\alpha))\)
, следовательно, \[\cos(\pi-\alpha)=-\cos\alpha, \qquad \sin(\pi-\alpha)=\sin\alpha\]
Таким образом доказываются и другие формулы, называемые формулами приведения : \[{\large{\begin{array}{l|r} \hline \sin(\pi-\alpha)=\sin\alpha & \cos(\pi-\alpha)=-\cos\alpha\\ \sin(\pi+\alpha)=-\sin\alpha & \cos(\pi+\alpha)=-\cos\alpha\\ \sin(2\pi\pm\alpha)=\pm\sin\alpha & \cos (2\pi\pm\alpha)=\cos\alpha\\ \sin \left(\dfrac{\pi}2\pm\alpha\right)=\cos\alpha & \cos\left(\dfrac{\pi}2\pm\alpha\right)=\pm\sin\alpha\\ \hline \end{array}}}\]
С помощью этих формул можно найти синус или косинус любого угла, сведя это значение к синусу или косинусу угла из \(I\) четверти.
Таблица синусов, косинусов, тангенсов и котангенсов углов из первой четверти:
\[{\large{\begin{array}{|c|c|c|c|c|c|}
\hline &&&&&\\[-17pt]
& \quad 0 \quad (0^ \circ)& \quad \dfrac{\pi}6 \quad (30^\circ)
& \quad \dfrac{\pi}4
\quad (45^\circ) & \quad \dfrac{\pi}3 \quad (60^\circ)& \quad \dfrac{\pi}2 \quad
(90^\circ) \\
&&&&&\\[-17pt]
\hline \sin & 0 &\frac12&\frac{\sqrt2}2&\frac{\sqrt3}2&1\\
\hline \cos &1&\frac{\sqrt3}2&\frac{\sqrt2}2&\frac12&0\\
\hline \mathrm{tg} &0 &\frac{\sqrt3}3&1&\sqrt3&\infty\\
\hline \mathrm{ctg} &\infty &\sqrt3&1&\frac{\sqrt3}3&0\\
\hline
\end{array}}}\]
Заметим, что данные значения были выведены в разделе “Геометрия на плоскости (планиметрия). Часть II” в теме “Начальные сведения о синусе, косинусе, тангенсе и котангенсе”.
Пример 5. Найдите \(\sin{\dfrac{3\pi}4}\) .
Преобразуем угол: \(\dfrac{3\pi}4=\dfrac{4\pi-\pi}{4}=\pi-\dfrac{\pi}4\)
Таким образом, \(\sin{\dfrac{3\pi}4}=\sin\left(\pi-\dfrac{\pi}4\right)=\sin\dfrac{\pi}4=\dfrac{\sqrt2}2\) .
\(\blacktriangleright\) Для упрощения запоминания и использования формул приведения можно следовать следующему правилу.
Случай 1. \(n\cdot \pi\pm \alpha\) \[\sin(n\cdot \pi\pm \alpha)=\bigodot \sin\alpha\] \[\cos(n\cdot \pi\pm \alpha)=\bigodot \cos\alpha\]
Знак угла можно найти, определив, в какой четверти он находится. Пользуясь таким правилом, предполагаем, что угол \(\alpha\) находится в \(I\) четверти.
Случай 2. Если угол можно представить в виде , где \(n\in\mathbb{N}\) , то \[\sin(n\cdot \pi+\dfrac{\pi}2\pm \alpha)=\bigodot \cos\alpha\] где на месте \(\bigodot\) стоит знак синуса угла \(n\cdot \pi\pm \alpha\) . \[\cos(n\cdot \pi+\dfrac{\pi}2\pm \alpha)=\bigodot \sin\alpha\] где на месте \(\bigodot\) стоит знак косинуса угла \(n\cdot \pi\pm \alpha\) .
Знак определяется таким же образом, как и в случае \(1\) .
Заметим, что в первом случае функция остается неизменной, а во втором случае - меняется (говорят, что функция меняется на кофункцию).
Пример 6. Найти \(\sin \dfrac{13\pi}{3}\) .
Преобразуем угол: \(\dfrac{13\pi}{3}=\dfrac{12\pi+\pi}{3}=4\pi+\dfrac{\pi}3\) , следовательно, \(\sin \dfrac{13\pi}{3}=\sin \left(4\pi+\dfrac{\pi}3\right)=\sin\dfrac{\pi}3=\dfrac{\sqrt3}2\)
Пример 7. Найти \(\cos \dfrac{17\pi}{6}\) .
Преобразуем угол: \(\dfrac{17\pi}{6}=\dfrac{18\pi-\pi}{6}=3\pi-\dfrac{\pi}6\)
, следовательно, \(\cos \dfrac{17\pi}{6}=\cos
\left(3\pi-\dfrac{\pi}6\right)=-\cos\dfrac{\pi}6=-\dfrac{\sqrt3}2\)
\(\blacktriangleright\)
Область значений синуса и косинуса
.
Т.к. координаты \(x_{\alpha}\)
и \(y_{\alpha}\)
любой точки \(P_{\alpha}\)
на единичной окружности находятся в пределах от \(-1\)
до \(1\)
, а \(\cos\alpha\)
и \(\sin\alpha\)
- абсцисса и ордината соответственно этой точки, то \[{\large{-1\leq \cos\alpha\leq 1 ,\qquad -1\leq\sin\alpha\leq 1}}\]

Из прямоугольного треугольника по теореме Пифагора имеем: \(x^2_{\alpha}+y^2_{\alpha}=1^2\)
Т.к. \(x_{\alpha}=\cos\alpha,\ y_{\alpha}=\sin\alpha \Rightarrow\)
\[{\large{\sin^2\alpha+\cos^2\alpha=1}} - \textbf{основное тригонометрическое тождество (ОТТ)}\]
\(\blacktriangleright\) Тангенс и котангенс .
Т.к. \(\mathrm{tg}\,\alpha=\dfrac{\sin\alpha}{\cos\alpha}, \cos\alpha\ne 0\)
\(\mathrm{ctg}\,\alpha=\dfrac{\cos\alpha}{\sin\alpha}, \sin\alpha\ne 0\) , то:
1) \({\large{\mathrm{tg}\,\alpha\cdot \mathrm{ctg}\,\alpha=1, \cos\alpha\ne 0, \sin\alpha \ne 0}}\)
2) тангенс и котангенс положительны в \(I\) и \(III\) четвертях и отрицательны в \(II\) и \(IV\) четвертях.
3) область значений тангенса и котангенса - все вещественные числа, т.е. \(\mathrm{tg}\,\alpha\in\mathbb{R}, \ \mathrm{ctg}\,\alpha\in\mathbb{R}\)
4) для тангенса и котангенса также определены формулы приведения.
Случай 1. \[\mathrm{tg}\,(n\cdot \pi\pm \alpha)=\bigodot \mathrm{tg}\,\alpha\] где на месте \(\bigodot\) стоит знак тангенса угла \(n\cdot \pi\pm \alpha\) (\(\cos\alpha\ne 0\) ). \[\mathrm{ctg}\,(n\cdot \pi\pm \alpha)=\bigodot \mathrm{ctg}\,\alpha\] где на месте \(\bigodot\) стоит знак котангенса угла \(n\cdot \pi\pm \alpha\) (\(\sin\alpha\ne 0\) ).
Случай 2. Если угол можно представить в виде \(n\cdot \pi+\dfrac{\pi}2\pm\alpha\) , где \(n\in\mathbb{N}\) , то \[\mathrm{tg}\,(n\cdot \pi+\dfrac{\pi}2\pm \alpha)=\bigodot \mathrm{ctg}\,\alpha\] где на месте \(\bigodot\) стоит знак тангенса угла \(n\cdot \pi\pm \alpha\) (\(\sin\alpha\ne 0\) ). \[\mathrm{ctg}\,(n\cdot \pi+\dfrac{\pi}2\pm \alpha)=\bigodot \mathrm{tg}\,\alpha\] где на месте \(\bigodot\) стоит знак котангенса угла \(n\cdot \pi\pm \alpha\) (\(\cos\alpha\ne 0\) ).
5) ось тангенсов проходит через точку \((1;0)\)
параллельно оси синусов, причем положительное направление оси тангенсов совпадает с положительным направлением оси синусов;
ось котангенсов - через точку \((0;1)\)
параллельно оси косинусов, причем положительное направление оси котангенсов совпадает с положительным направлением оси косинусов.
Доказательство этого факта приведем на примере оси тангенсов.
\(\triangle OP_{\alpha}K \sim \triangle AOB \Rightarrow \dfrac{P_{\alpha}K}{OK}=\dfrac{BA}{OB} \Rightarrow \dfrac{\sin\alpha}{\cos\alpha}=\dfrac{BA}1 \Rightarrow BA=\mathrm{tg}\,\alpha\) .
Таким образом, если точку \(P_{\alpha}\)
соединить прямой с центром окружности, то эта прямая пересечет линию тангенсов в точке, значение которой равно \(\mathrm{tg}\,\alpha\)
.
6) из основного тригонометрического тождества вытекают следующие формулы: \
Первую формулу получают делением правой и левой частей ОТТ на \(\cos^2\alpha\)
, вторую - делением на \(\sin^2\alpha\)
.
Обращаем внимание, что тангенс не определен в углах, где косинус равен нулю (это \(\alpha=\dfrac{\pi}2+\pi n, n\in\mathbb{Z}\)
);
котангенс не определен в углах, где синус равен нулю (это \(\alpha=\pi+\pi n, n\in\mathbb{Z}\)
).
\(\blacktriangleright\) Четность косинуса и нечетность синуса, тангенса, котангенса .
Напомним, что функция \(f(x)\) называется четной, если \(f(-x)=f(x)\) .
Функция называется нечетной, если \(f(-x)=-f(x)\) .
По окружности видно, что косинус угла \(\alpha\)
равен косинусу угла \(-\alpha\)
при любых значениях \(\alpha\)
:
Таким образом, косинус - четная функция, значит, верна формула \[{\Large{\cos(-x)=\cos x}}\]
По окружности видно, что синус угла \(\alpha\)
противоположен синусу угла \(-\alpha\)
при любых значениях \(\alpha\)
:
Таким образом, синус - нечетная функция, значит, верна формула \[{\Large{\sin(-x)=-\sin x}}\]
Тангенс и котангенс также нечетные функции: \[{\Large{\mathrm{tg}\,(-x)=-\mathrm{tg}\,x}}\] \[{\Large{\mathrm{ctg}\,(-x)=-\mathrm{ctg}\,x}}\]
Т.к. \(\mathrm{tg}\,(-x)=\dfrac{\sin (-x)}{\cos(-x)}=\dfrac{-\sin x}{\cos x}=-\mathrm{tg}\,x \qquad \mathrm{ctg}\,(-x)=\dfrac{\cos(-x)}{\sin(-x)}=-\mathrm{ctg}\,x\) )
Как показывает практика, один из сложнейших разделов математики, который встречается школьникам в ЕГЭ, - тригонометрия. С наукой о соотношениях сторон в треугольниках начинают знакомиться в 8 классе. Уравнения данного типа содержат переменную под знаком тригонометрических функций. Несмотря на то, что простейшие из них: \(sin x = a\) , \(cos x = a\) , \(tg x = a\) , \(ctg x = a\) - знакомы практически каждому школьнику, их выполнение зачастую вызывает сложности.
В ЕГЭ по математике профильного уровня правильно решенное задание по тригонометрии оценивается очень высоко. Школьник может получить до 4 первичных баллов за верно выполненную задачу из данного раздела. Для этого искать к ЕГЭ шпаргалки по тригонометрии практически бессмысленно. Наиболее разумное решение - хорошо подготовиться к экзамену.
Как это сделать?
Для того чтобы тригонометрия в ЕГЭ по математике вас не пугала, воспользуйтесь при подготовке нашим порталом. Это удобно, просто и эффективно. В данном разделе нашего образовательного портала, открытом для учащихся как Москвы, так и других городов, представлены доступно изложенный теоретический материал и формулы по тригонометрии для ЕГЭ. Также ко всем математическим определениям мы подобрали примеры с подробным описанием хода их решения.
После изучения теории по разделу «Тригонометрия» при подготовке к ЕГЭ рекомендуем перейти в «Каталоги», для того чтобы полученные знания лучше усвоились. Здесь вы сможете выбрать задачи по интересующей теме и просмотреть их решения. Таким образом, повторение теории по тригонометрии в ЕГЭ будет максимально эффективным.
Что нужно знать?
Прежде всего необходимо выучить значения \(sin\) , \(cos\) , \(tg\) , \(ctg\) острых углов от \(0°\) до \(90°\) . Также при подготовке к ЕГЭ в Москве стоит запомнить основные методы решения заданий по тригонометрии. Следует учесть, что, выполняя задачи, вы должны привести уравнение к простейшему виду. Сделать это можно следующим образом:
- разложив уравнение на множители;
- заменив переменную (сведение к алгебраическим уравнениям);
- приведя к однородному уравнению;
- перейдя к половинному углу;
- преобразовав произведения в сумму;
- введя вспомогательный угол;
- использовав способ универсальной подстановки.
При этом чаще всего учащемуся приходится в ходе решения использовать несколько из перечисленных методов.
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля - до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.