وزارة التعليم العام والمهني

جامعة ولاية سوتشي للسياحة

وأعمال المنتجع

المعهد التربوي

كلية الرياضيات

قسم الرياضيات العامة

عمل التخرج

متسلسلة فورييه وتطبيقاتها

في الفيزياء الرياضية.

أكمله: طالب في السنة الخامسة

التوقيع على التعليم بدوام كامل

التخصص 010100

"الرياضيات"

كاسبيروفا إن إس.

رقم هوية الطالب 95471

المشرف العلمي: أستاذ مشارك، مرشح.

التوقيع الفني علوم

بوزين ب.

سوتشي، 2000

1 المقدمة.

2. مفهوم متسلسلة فورييه.

2.1. تحديد معاملات سلسلة فورييه.

2.2. تكاملات الوظائف الدورية.

3. علامات تقارب متسلسلة فورييه.

3.1. أمثلة على توسيع الوظائف في سلسلة فورييه.

4. ملاحظة حول توسيع سلسلة فورييه للدالة الدورية

5. سلسلة فورييه للوظائف الزوجية والفردية.

6. سلسلة فورييه للوظائف ذات الفترة 2 ل .

7. توسيع سلسلة فورييه للدالة غير الدورية.

مقدمة.

جان بابتيست جوزيف فورييه - عالم رياضيات فرنسي، عضو أكاديمية باريس للعلوم (1817).

تتعلق أعمال فورييه الأولى بالجبر. بالفعل في محاضرات عام 1796، قدم نظرية حول عدد الجذور الحقيقية لمعادلة جبرية تقع بين حدود معينة (نُشرت عام 1820)، سميت باسمه؛ تم الحصول على حل كامل لعدد الجذور الحقيقية لمعادلة جبرية في عام 1829 بواسطة J.S.F. بالاعتداء. في عام 1818، حقق فورييه في مسألة شروط تطبيق طريقة الحل العددي للمعادلات التي طورها نيوتن، دون أن يعرف النتائج المماثلة التي حصل عليها عالم الرياضيات الفرنسي جي آر. موريلم. نتيجة عمل فورييه على الطرق العددية لحل المعادلات هو "تحليل المعادلات المحددة"، الذي نشر بعد وفاته في عام 1831.

كان المجال الرئيسي لدراسة فورييه هو الفيزياء الرياضية. وفي عامي 1807 و1811، قدم أول اكتشافاته حول نظرية انتشار الحرارة في المواد الصلبة إلى أكاديمية باريس للعلوم، وفي عام 1822 نشر العمل الشهير “النظرية التحليلية للحرارة”، والذي لعب دورًا رئيسيًا في التاريخ اللاحق للحرارة. الرياضيات. هذه هي النظرية الرياضية للتوصيل الحراري. ونظرًا لعمومية الطريقة، فقد أصبح هذا الكتاب مصدرًا لجميع الأساليب الحديثة في الفيزياء الرياضية. في هذا العمل، اشتق فورييه المعادلة التفاضلية للتوصيل الحراري وطوّر الأفكار التي أوضحها د. بيرنولي سابقًا، وطوّر طريقة لفصل المتغيرات (طريقة فورييه) لحل معادلة الحرارة في ظل ظروف حدودية معينة، والتي طبقها على عدد الحالات الخاصة (مكعب، اسطوانة، الخ). تعتمد هذه الطريقة على تمثيل الدوال بواسطة متسلسلة فورييه المثلثية.

أصبحت متسلسلة فورييه الآن أداة متطورة في نظرية المعادلات التفاضلية الجزئية لحل مشاكل القيمة الحدودية.

1. مفهوم متسلسلة فورييه.(ص 94، أوفارينكوف)

تلعب متسلسلة فورييه دورًا مهمًا في الفيزياء الرياضية، ونظرية المرونة، والهندسة الكهربائية، وخاصة حالتها الخاصة - متسلسلة فورييه المثلثية.

المتسلسلة المثلثية هي سلسلة من الشكل

أو رمزياً:

(1)

حيث ω، a 0، a 1، …، a n، …، b 0، b 1، …، b n، … هي أرقام ثابتة (ω>0).

وقد أدت بعض المشاكل في الفيزياء تاريخيًا إلى دراسة مثل هذه المتسلسلات، على سبيل المثال، مشكلة اهتزازات الأوتار (القرن الثامن عشر)، ومشكلة الانتظام في ظواهر التوصيل الحراري، وما إلى ذلك. وفي التطبيقات، النظر في المتسلسلة المثلثية , يرتبط في المقام الأول بمهمة تمثيل حركة معينة، الموصوفة بالمعادلة y = ƒ(χ)، in

في شكل مجموع أبسط التذبذبات التوافقية، والتي غالبًا ما تؤخذ بعدد كبير لا نهائي، أي كمجموع سلسلة من الشكل (1).

وبالتالي، نصل إلى المشكلة التالية: لمعرفة ما إذا كانت هناك سلسلة (1) لدالة معينة ƒ(x) في فترة زمنية معينة تتقارب في هذه الفترة مع هذه الوظيفة. إذا كان ذلك ممكنا، فإنهم يقولون أنه في هذه الفترة يتم توسيع الدالة ƒ(x) إلى سلسلة مثلثية.

تتقارب السلسلة (1) عند نقطة ما × 0، بسبب دورية الدوال

(n=1,2,..) ستكون متقاربة في جميع نقاط النموذج (m أي عدد صحيح)، وبالتالي سيكون مجموعها S(x) (في منطقة تقارب المتسلسلة ) دالة دورية: إذا كان S n ( x) هو المجموع الجزئي n لهذه السلسلة، فلدينا

وبالتالي

، أي S(x 0 +T)=S(x 0). لذلك، عند الحديث عن توسيع بعض الوظائف ƒ(x) إلى سلسلة من النموذج (1)، سنفترض أن ƒ(x) هي دالة دورية.

2. تحديد معاملات السلسلة باستخدام صيغ فورييه.

دع الدالة الدورية ƒ(x) ذات الفترة 2π تكون ممثلة بسلسلة مثلثية تتقارب مع دالة معينة في الفترة (-π، π)، أي هي مجموع هذه السلسلة:

. (2)

لنفترض أن تكامل الدالة على الجانب الأيسر من هذه المساواة يساوي مجموع تكاملات حدود هذه المتسلسلة. سيكون هذا صحيحًا إذا افترضنا أن سلسلة الأعداد المكونة من معاملات سلسلة مثلثية معينة متقاربة تمامًا، أي أن سلسلة الأعداد الموجبة تتقارب

(3)

السلسلة (1) قابلة للتكبير ويمكن دمجها مصطلحًا تلو الآخر في الفترة (-π، π). لندمج طرفي المساواة (2):

دعونا نقيم بشكل منفصل كل تكامل يظهر على الجانب الأيمن:

, .

هكذا،

، أين

. (4)

تقدير معاملات فورييه.(بوغروف)

النظرية 1. دع الدالة ƒ(x) للفترة 2π لها مشتق مستمر ƒ ( ق) (خ) النظام s، مما يلبي عدم المساواة على المحور الحقيقي بأكمله:

│ ƒ (ق) (س)│≥ م ث ; (5)

ثم معاملات فورييه للدالة ƒ تلبية عدم المساواة

(6)

دليل. التكامل بالأجزاء ومراعاة ذلك

ƒ(-π) = ƒ(π)، لدينا

تكامل الجانب الأيمن من (7) بالتتابع، مع الأخذ في الاعتبار أن المشتقات ƒ ΄، …، ƒ (s-1) متصلة وتأخذ نفس القيم عند النقاط t = -π و t = π، كما وكذلك التقدير (5) نحصل على التقدير الأول (6).

ويتم الحصول على التقدير الثاني (6) بطريقة مماثلة.

النظرية 2. بالنسبة لمعاملات فورييه ƒ(x) فإن عدم المساواة التالية يحمل:

(8)

دليل. لدينا

وهي بالفعل مملة جدًا. وأشعر أن اللحظة قد حانت عندما حان الوقت لاستخراج سلع معلبة جديدة من الاحتياطيات الاستراتيجية للنظرية. هل من الممكن توسيع الوظيفة إلى سلسلة بطريقة أخرى؟ على سبيل المثال، التعبير عن قطعة مستقيمة من حيث الجيب وجيب التمام؟ يبدو الأمر لا يصدق، ولكن مثل هذه الوظائف التي تبدو بعيدة يمكن أن تكون كذلك
"إعادة التوحيد". بالإضافة إلى الدرجات المألوفة من الناحية النظرية والتطبيقية، هناك طرق أخرى لتوسيع دالة إلى سلسلة.

في هذا الدرس سوف نتعرف على متسلسلة فورييه المثلثية، ونتطرق إلى مسألة تقاربها ومجموعها، وبالطبع، سنحلل العديد من الأمثلة على مفكوك الدوال في متسلسلة فورييه. أردت بصدق أن أسمي المقال "متسلسلة فورييه للدمى"، ولكن هذا سيكون مخادعًا، لأن حل المشكلات يتطلب معرفة بفروع أخرى من التحليل الرياضي وبعض الخبرة العملية. ولذلك فإن الديباجة سوف تشبه تدريب رواد الفضاء =)

أولا، يجب عليك التعامل مع دراسة مواد الصفحة في شكل ممتاز. نعسان ومرتاح ورصين. بدون مشاعر قوية بشأن كسر ساق الهامستر والأفكار المهووسة حول مصاعب الحياة بالنسبة لأسماك الزينة. ليس من الصعب فهم سلسلة فورييه، لكن المهام العملية تتطلب ببساطة تركيزًا متزايدًا من الاهتمام - ومن الناحية المثالية، يجب عليك فصل نفسك تمامًا عن المحفزات الخارجية. ويتفاقم الوضع بسبب عدم وجود طريقة سهلة للتحقق من الحل والإجابة. وبالتالي، إذا كانت صحتك أقل من المتوسط، فمن الأفضل أن تفعل شيئا أسهل. هل هذا صحيح؟

ثانيا، قبل الطيران إلى الفضاء، من الضروري دراسة لوحة العدادات الخاصة بالمركبة الفضائية. لنبدأ بقيم الوظائف التي يجب النقر عليها على الجهاز:

لأي قيمة طبيعية:

1) . في الواقع، يقوم الشكل الجيبي "بغرز" المحور السيني من خلال كل "باي":
. في حالة القيم السالبة للوسيطة فإن النتيجة بالطبع ستكون نفسها: .

2) . ولكن لم يكن الجميع يعرف هذا. جيب التمام "pi" هو ما يعادل "الوامض":

الحجة السلبية لا تغير الأمر: .

ربما هذا يكفي.

وثالثًا، أعزائي طاقم رواد الفضاء، يجب أن تكونوا قادرين على... دمج.
على وجه الخصوص، بثقة تدرج الدالة تحت العلامة التفاضلية, دمج تدريجيويكون في سلام مع صيغة نيوتن-لايبنتز. لنبدأ بتمارين ما قبل الرحلة المهمة. لا أنصح بشكل قاطع بتخطيه، حتى لا تتعرض لانعدام الوزن لاحقًا:

مثال 1

حساب التكاملات المحددة

حيث يأخذ القيم الطبيعية.

حل: يتم التكامل على المتغير "x" وفي هذه المرحلة يعتبر المتغير المنفصل "en" ثابتا. في جميع التكاملات ضع الدالة تحت العلامة التفاضلية:

تبدو النسخة القصيرة من الحل الذي سيكون من الجيد استهدافه كما يلي:

فلنعتاد على ذلك:

النقاط الأربع المتبقية هي لوحدك. حاول التعامل مع المهمة بضمير حي واكتب التكاملات بطريقة قصيرة. نماذج من الحلول في نهاية الدرس.

بعد أداء تمارين الجودة، نرتدي بدلات الفضاء
والاستعداد للبدء!

توسيع الدالة إلى سلسلة فورييه على الفاصل الزمني

النظر في بعض الوظائف التي عازمعلى الأقل لفترة من الوقت (وربما لفترة أطول). إذا كانت هذه الدالة قابلة للتكامل على الفترة، فيمكن توسيعها إلى دالة مثلثية سلسلة فورييه:
، أين ما يسمى معاملات فورييه.

في هذه الحالة يتم استدعاء الرقم فترة التحلل، والرقم هو نصف عمر التحلل.

من الواضح أنه في الحالة العامة، تتكون سلسلة فورييه من جيب التمام وجيب التمام:

في الواقع، دعونا نكتب ذلك بالتفصيل:

عادةً ما يُكتب الحد الصفري للمتسلسلة بالصيغة .

يتم حساب معاملات فورييه باستخدام الصيغ التالية:

أفهم جيدًا أن أولئك الذين بدأوا دراسة الموضوع ما زالوا غير واضحين بشأن المصطلحات الجديدة: فترة التحلل, نصف دورة, معاملات فورييهإلخ. لا داعي للذعر، فهذا لا يمكن مقارنته بالإثارة قبل الذهاب إلى الفضاء الخارجي. دعونا نفهم كل شيء في المثال التالي، قبل تنفيذه الذي من المنطقي طرح أسئلة عملية ملحة:

ما الذي يجب عليك فعله في المهام التالية؟

قم بتوسيع الدالة إلى سلسلة فورييه. بالإضافة إلى ذلك، غالبًا ما يكون من الضروري تصوير رسم بياني لدالة، ورسم بياني لمجموع سلسلة، ومجموع جزئي، وفي حالة التخيلات الأستاذية المتطورة، افعل شيئًا آخر.

كيفية توسيع وظيفة إلى سلسلة فورييه؟

في الأساس، تحتاج إلى العثور عليها معاملات فورييهأي يؤلف ويحسب ثلاثة تكامل محدد.

يرجى إعادة كتابة الشكل العام لسلسلة فورييه وصيغ العمل الثلاث في دفتر ملاحظاتك. أنا سعيد جدًا لأن بعض زوار الموقع يحققون حلم طفولتهم في أن يصبحوا رواد فضاء أمام عيني مباشرة =)

مثال 2

قم بتوسيع الدالة إلى سلسلة فورييه على الفاصل الزمني. أنشئ رسمًا بيانيًا، رسمًا بيانيًا لمجموع المتسلسلة والمجموع الجزئي.

حل: الجزء الأول من المهمة هو توسيع الدالة إلى سلسلة فورييه.

البداية قياسية، تأكد من كتابة ما يلي:

في هذه المشكلة، تكون فترة التوسيع نصف فترة.

دعونا نوسع الدالة إلى متسلسلة فورييه على الفترة:

وباستخدام الصيغ المناسبة نجد معاملات فورييه. الآن نحن بحاجة إلى تكوين وحساب ثلاثة تكامل محدد. وللتيسير سأقوم بترقيم النقاط:

1) التكامل الأول هو الأبسط، ولكنه يتطلب أيضًا مقل العيون:

2) استخدم الصيغة الثانية:

وهذا التكامل معروف جيداً يأخذها قطعة قطعة:

تستخدم عند العثور عليها طريقة إدراج دالة تحت العلامة التفاضلية.

في المهمة قيد النظر، يكون الأمر أكثر ملاءمة للاستخدام على الفور صيغة التكامل بالأجزاء في تكامل محدد :

بضع ملاحظات فنية. أولا، بعد تطبيق الصيغة يجب أن يكون التعبير بأكمله محاطًا بأقواس كبيرةلأنه يوجد ثابت قبل التكامل الأصلي. دعونا لا نفقدها! يمكن توسيع الأقواس في أي خطوة أخرى؛ لقد فعلت ذلك كحل أخير. في "القطعة" الأولى لقد أظهرنا اهتمامًا شديدًا بالاستبدال، كما ترون، ولم يتم استخدام الثابت، وتم استبدال حدود التكامل في المنتج. تم تمييز هذا الإجراء بين قوسين معقوفين. حسنًا، أنت على دراية بتكامل "الجزء" الثاني من الصيغة من مهمة التدريب؛-)

والأهم من ذلك - التركيز الشديد!

3) نبحث عن معامل فورييه الثالث:

يتم الحصول على قريب من التكامل السابق، وهو أيضا يدمج بشكل مجزأ:

هذا المثال أكثر تعقيدًا بعض الشيء، وسأعلق على الخطوات الإضافية خطوة بخطوة:

(1) التعبير محاط بالكامل بين قوسين كبيرين. لم أكن أريد أن أبدو مملا، فهم يفقدون الثابت في كثير من الأحيان.

(٢) في هذه الحالة، قمت على الفور بفتح هذه الأقواس الكبيرة. انتباه خاصنحن نكرس أنفسنا لـ "القطعة" الأولى: يدخن المستمر على الهامش ولا يشارك في استبدال حدود التكامل (و) في المنتج. ونظرًا لفوضى السجل، يُنصح مرة أخرى بتسليط الضوء على هذا الإجراء بين قوسين معقوفين. مع "القطعة" الثانية كل شيء أبسط: هنا ظهر الكسر بعد فتح الأقواس الكبيرة، والثابت - نتيجة لتكامل التكامل المألوف؛-)

(3) نجري التحويلات بين قوسين مربعين، وفي التكامل الصحيح نعوض بحدود التكامل.

(4) نزيل "الضوء الوامض" من الأقواس المربعة : ، ثم نفتح الأقواس الداخلية : .

(5) نحذف 1 و-1 بين قوسين ونقوم بالتبسيط النهائي.

وأخيرًا، تم العثور على معاملات فورييه الثلاثة:

دعونا نستبدلهم في الصيغة :

وفي الوقت نفسه، لا تنسى أن تقسم إلى النصف. في الخطوة الأخيرة، يتم أخذ الثابت ("ناقص اثنين")، الذي لا يعتمد على "en"، خارج المجموع.

وهكذا، حصلنا على توسيع الدالة إلى سلسلة فورييه على الفترة:

دعونا ندرس مسألة تقارب متسلسلة فورييه. وسأشرح النظرية على وجه الخصوص نظرية ديريشليت، حرفيا "على الأصابع"، لذلك إذا كنت بحاجة إلى صيغ صارمة، فيرجى الرجوع إلى الكتاب المدرسي حول التحليل الرياضي (على سبيل المثال، المجلد الثاني من بوهان؛ أو المجلد الثالث من فيشتنهولتز، لكنه أكثر صعوبة).

يتطلب الجزء الثاني من المشكلة رسم رسم بياني، رسم بياني لمجموع سلسلة، ورسم بياني لمجموع جزئي.

الرسم البياني للوظيفة هو المعتاد خط مستقيم على متن الطائرة، والتي يتم رسمها بخط منقط أسود:

دعونا معرفة مجموع السلسلة. كما تعلمون، سلسلة الوظائف تتلاقى مع الوظائف. في حالتنا، سلسلة فورييه التي تم إنشاؤها لأي قيمة "x"سوف تتقارب مع الوظيفة، والتي تظهر باللون الأحمر. هذه الوظيفة تتسامح تمزقات من النوع الأولفي نقاط، ولكن يتم تعريفها أيضًا (النقاط الحمراء في الرسم)

هكذا: . من السهل أن نرى أنها مختلفة بشكل ملحوظ عن الوظيفة الأصلية، وهذا هو السبب في الإدخال يتم استخدام التلدة بدلا من علامة يساوي.

دعونا ندرس خوارزمية مناسبة لبناء مجموع السلسلة.

على الفاصل الزمني المركزي، تتقارب سلسلة فورييه مع الدالة نفسها (يتزامن الجزء الأحمر المركزي مع الخط الأسود المنقط للدالة الخطية).

الآن دعونا نتحدث قليلاً عن طبيعة التوسع المثلثي قيد النظر. سلسلة فورييه يتم تضمين الوظائف الدورية فقط (الثابت، وجيب التمام، وجيب التمام)، وبالتالي فإن مجموع السلسلة هي أيضا وظيفة دورية.

ماذا يعني هذا في مثالنا المحدد؟ وهذا يعني أن مجموع السلسلة –بالتأكيد دوريةويجب تكرار الجزء الأحمر من الفاصل الزمني إلى ما لا نهاية على اليسار واليمين.

أعتقد أن معنى عبارة "فترة التحلل" أصبح الآن واضحا. بكل بساطة، في كل مرة يتكرر الوضع مرارا وتكرارا.

ومن الناحية العملية، عادة ما يكفي تصوير ثلاث فترات من التحلل، كما هو الحال في الرسم. حسنًا، وأيضًا "جذوع الأشجار" للفترات المجاورة - بحيث يكون من الواضح أن الرسم البياني مستمر.

ذات أهمية خاصة هي نقاط الانقطاع من النوع الأول. في مثل هذه النقاط، تتقارب سلسلة فورييه إلى قيم معزولة، والتي تقع بالضبط في منتصف "قفزة" الانقطاع (النقاط الحمراء في الرسم). كيفية معرفة إحداثيات هذه النقاط؟ أولاً، دعونا نجد إحداثيات "الطابق العلوي": للقيام بذلك، نحسب قيمة الدالة عند أقصى يمين الفترة المركزية للتوسع: . لحساب إحداثيات "الطابق السفلي"، أسهل طريقة هي أخذ القيمة الموجودة في أقصى اليسار للفترة نفسها: . إحداثيات القيمة المتوسطة هي الوسط الحسابي لمجموع "الأعلى والأسفل": . الحقيقة اللطيفة هي أنه عند إنشاء رسم، سترى على الفور ما إذا كان الوسط قد تم حسابه بشكل صحيح أم غير صحيح.

لنقم ببناء مجموع جزئي للمتسلسلة وفي نفس الوقت نكرر معنى مصطلح "التقارب". الدافع معروف أيضًا من الدرس مجموع سلسلة أرقام. دعونا نصف ثروتنا بالتفصيل:

لتكوين مجموع جزئي، عليك كتابة صفر + حدين آخرين من السلسلة. إنه،

في الرسم، يظهر الرسم البياني للدالة باللون الأخضر، وكما ترون، فإنه "يغلف" المبلغ بالكامل بإحكام شديد. إذا أخذنا في الاعتبار مجموعًا جزئيًا لخمسة حدود من السلسلة، فإن الرسم البياني لهذه الدالة سوف يقترب من الخطوط الحمراء بشكل أكثر دقة؛ إذا كان هناك مائة حد، فسوف يندمج "الثعبان الأخضر" تمامًا مع الأجزاء الحمراء، إلخ. وهكذا فإن متسلسلة فورييه تتقارب إلى مجموعها.

ومن المثير للاهتمام أن نلاحظ أن أي مبلغ جزئي هو وظيفة مستمرةومع ذلك، فإن المجموع الإجمالي للسلسلة لا يزال متقطعا.

من الناحية العملية، ليس من النادر إنشاء رسم بياني للمجموع الجزئي. كيف افعلها؟ في حالتنا، من الضروري النظر في الدالة على المقطع، وحساب قيمها في نهايات المقطع وفي النقاط المتوسطة (كلما زاد عدد النقاط التي تضعها في الاعتبار، كلما كان الرسم البياني أكثر دقة). ثم يجب عليك وضع علامة على هذه النقاط على الرسم ورسم رسم بياني دقيق للفترة، ثم "تكراره" في فترات متجاورة. و إلا كيف؟ بعد كل شيء، التقريب هو أيضًا وظيفة دورية... ...يذكرني الرسم البياني الخاص به في بعض النواحي بإيقاع قلب منتظم على شاشة الجهاز الطبي.

إن تنفيذ البناء، بطبيعة الحال، ليس مريحًا للغاية، حيث يتعين عليك توخي الحذر الشديد، والحفاظ على دقة لا تقل عن نصف ملليمتر. ومع ذلك، سأسعد القراء الذين لا يشعرون بالراحة مع الرسم - في مشكلة "حقيقية"، ليس من الضروري دائمًا إجراء رسم؛ في حوالي 50٪ من الحالات، من الضروري توسيع الوظيفة إلى سلسلة فورييه وهذا كل شيء .

بعد الانتهاء من الرسم نكمل المهمة:

إجابة:

في العديد من المهام تعاني الوظيفة تمزق من النوع الأولالحق خلال فترة التحلل:

مثال 3

قم بتوسيع الدالة المعطاة في الفترة إلى سلسلة فورييه. ارسم رسمًا بيانيًا للدالة والمجموع الإجمالي للسلسلة.

يتم تحديد الوظيفة المقترحة بطريقة تدريجية (ولاحظ فقط على المقطع)ويتحمل تمزق من النوع الأولعند نقطة . هل من الممكن حساب معاملات فورييه؟ لا مشكلة. كلا الجانبين الأيسر والأيمن من الدالة قابلان للتكامل في فتراتهما، لذلك يجب تمثيل التكاملات في كل من الصيغ الثلاث كمجموع تكاملين. دعونا نرى، على سبيل المثال، كيف يتم ذلك لمعامل صفر:

وتبين أن التكامل الثاني يساوي الصفر، مما أدى إلى تقليل العمل، ولكن هذا ليس هو الحال دائمًا.

يتم وصف معاملي فورييه الآخرين بالمثل.

كيفية إظهار مجموع السلسلة؟ على الفاصل الزمني الأيسر، نرسم قطعة خط مستقيم، وعلى الفاصل الزمني - قطعة خط مستقيم (نسلط الضوء على قسم المحور بالخط العريض والغامق). أي أنه في فترة التوسيع، يتطابق مجموع المتسلسلة مع الدالة في كل مكان باستثناء ثلاث نقاط "سيئة". عند نقطة انقطاع الدالة، ستتقارب متسلسلة فورييه إلى قيمة معزولة، والتي تقع بالضبط في منتصف "قفزة" الانقطاع. ليس من الصعب رؤيته شفهيًا: الحد الأيسر: الحد الأيمن: ومن الواضح أن إحداثيات نقطة المنتصف هي 0.5.

نظرًا لدورية المجموع، يجب "مضاعفة" الصورة في الفترات المجاورة، على وجه الخصوص، يجب تصوير نفس الشيء على الفواصل الزمنية و . وفي الوقت نفسه، عند النقاط، ستتقارب متسلسلة فورييه مع القيم المتوسطة.

في الواقع، لا يوجد شيء جديد هنا.

حاول التعامل مع هذه المهمة بنفسك. نموذج تقريبي للتصميم النهائي ورسم في نهاية الدرس.

توسيع الدالة إلى سلسلة فورييه خلال فترة تعسفية

بالنسبة لفترة التوسع التعسفية، حيث "el" هو أي رقم موجب، تتميز صيغ متسلسلة فورييه ومعاملات فورييه بحجة أكثر تعقيدًا قليلاً للجيب وجيب التمام:

إذا، فسنحصل على صيغ الفترة التي بدأنا بها.

تم الحفاظ على الخوارزمية ومبادئ حل المشكلة بالكامل، ولكن التعقيد الفني للحسابات يزداد:

مثال 4

قم بتوسيع الدالة إلى سلسلة فورييه ورسم المجموع.

حل: في الواقع نظير للمثال رقم 3 مع تمزق من النوع الأولعند نقطة . في هذه المشكلة، تكون فترة التوسيع نصف فترة. يتم تعريف الدالة فقط على نصف الفترة، ولكن هذا لا يغير الأمر - من المهم أن يكون كلا جزأين الدالة قابلين للتكامل.

دعونا نوسع الدالة إلى متسلسلة فورييه:

بما أن الدالة غير متصلة عند الأصل، فمن الواضح أنه يجب كتابة كل معامل فورييه كمجموع تكاملين:

1) سأكتب التكامل الأول بأكبر قدر ممكن من التفاصيل:

2) ننظر بعناية إلى سطح القمر:

التكامل الثاني خذها قطعة قطعة:

ما الذي يجب أن ننتبه إليه جيدًا بعد أن نفتح استمرار الحل بعلامة النجمة؟

أولا، نحن لا نفقد التكامل الأول ، حيث نقوم بالتنفيذ على الفور الاشتراك في العلامة التفاضلية. ثانيا، لا تنسى الثابت المشؤوم قبل القوسين الكبيرين و لا تخلط بين العلاماتعند استخدام الصيغة . لا تزال الأقواس الكبيرة أكثر ملاءمة لفتحها فورًا في الخطوة التالية.

أما الباقي فهو مسألة تقنية؛ ولا يمكن أن يكون سبب الصعوبات إلا عدم كفاية الخبرة في حل التكاملات.

نعم، لم يكن عبثا أن الزملاء البارزين لعالم الرياضيات الفرنسي فورييه كانوا ساخطين - كيف تجرأ على ترتيب الدوال في سلسلة مثلثية؟! =) بالمناسبة، ربما يكون الجميع مهتمين بالمعنى العملي للمهمة المعنية. عمل فورييه بنفسه على نموذج رياضي للتوصيل الحراري، وبعد ذلك بدأ استخدام السلسلة التي تحمل اسمه لدراسة العديد من العمليات الدورية المرئية وغير المرئية في العالم المحيط. الآن، بالمناسبة، وجدت نفسي أفكر أنه ليس من قبيل الصدفة أنني قارنت الرسم البياني للمثال الثاني مع الإيقاع الدوري للقلب. ويمكن للمهتمين التعرف على التطبيق العملي تحويل فورييهفي مصادر الطرف الثالث. ...على الرغم من أنه من الأفضل عدم القيام بذلك - سيتم تذكره على أنه الحب الأول =)

3) مع الأخذ في الاعتبار الروابط الضعيفة المذكورة مرارا وتكرارا، دعونا ننظر إلى المعامل الثالث:

دعونا نتكامل بالأجزاء:

لنستبدل معاملات فورييه الموجودة في الصيغة ولا ننسى تقسيم معامل الصفر إلى النصف:

دعونا نرسم مجموع السلسلة. دعونا نكرر الإجراء بإيجاز: نرسم خطًا مستقيمًا على فترة، وخطًا مستقيمًا على فترة. إذا كانت قيمة "x" صفرًا، فإننا نضع نقطة في منتصف "قفزة" الفجوة و"نكرر" الرسم البياني للفترات المجاورة:

عند "تقاطعات" الفترات، سيكون المجموع أيضًا مساويًا لنقاط منتصف "قفزة" الفجوة.

مستعد. اسمحوا لي أن أذكرك أن الدالة نفسها يتم تعريفها حسب الشرط فقط على نصف فترة، ومن الواضح أنها تتطابق مع مجموع السلسلة على الفترات

إجابة:

في بعض الأحيان تكون الدالة المعطاة متعددة التعريف مستمرة خلال فترة التوسيع. أبسط مثال: . حل (انظر المجلد بوهان 2)كما في المثالين السابقين: بالرغم من ذلك استمرارية الوظيفةعند النقطة ، يتم التعبير عن كل معامل فورييه كمجموع تكاملين.

على فترة التحلل نقاط الانقطاع من النوع الأولو/أو قد يكون هناك المزيد من نقاط "التقاطع" في الرسم البياني (اثنتان، وثلاثة، وبشكل عام أي نقطة تقاطع). أخيركمية). إذا كانت الدالة قابلة للتكامل في كل جزء، فهي أيضًا قابلة للتوسيع في سلسلة فورييه. لكن من التجربة العملية لا أتذكر مثل هذا الشيء القاسي. ومع ذلك، هناك مهام أكثر صعوبة من تلك التي تم تناولها للتو، وفي نهاية المقال توجد روابط لسلسلة فورييه ذات التعقيد المتزايد للجميع.

في هذه الأثناء، دعونا نسترخي ونتكئ على كراسينا ونتأمل المساحات اللامتناهية من النجوم:

مثال 5

قم بتوسيع الدالة إلى سلسلة فورييه على الفاصل الزمني ورسم مجموع السلسلة.

في هذه المشكلة الوظيفة مستمرعلى نصف فترة التوسع، مما يبسط الحل. كل شيء مشابه جدًا للمثال رقم 2. ليس هناك مفر من سفينة الفضاء - عليك أن تقرر =) نموذج تصميم تقريبي في نهاية الدرس، مرفق جدول زمني.

توسيع سلسلة فورييه للوظائف الزوجية والفردية

مع الوظائف الزوجية والفردية، يتم تبسيط عملية حل المشكلة بشكل ملحوظ. وهذا هو السبب. لنعد إلى توسيع دالة في متسلسلة فورييه بفترة "اثنين باي" والفترة التعسفية “اثنين إل” .

لنفترض أن وظيفتنا زوجية. الحد العام للسلسلة، كما ترون، يحتوي على جيب التمام وجيب التمام الفردية. وإذا كنا نقوم بفك دالة زوجية، فلماذا نحتاج إلى جيوب غريبة؟! دعونا نعيد ضبط المعامل غير الضروري: .

هكذا، يمكن توسيع الدالة الزوجية إلى سلسلة فورييه فقط في جيب التمام:

بسبب ال تكاملات الدوال الزوجيةعلى طول قطعة التكامل المتناظرة بالنسبة إلى الصفر، يمكن مضاعفتها، ثم يتم تبسيط معاملات فورييه المتبقية.

بالنسبة للفجوة:

لفترة تعسفية:

تتضمن أمثلة الكتب المدرسية التي يمكن العثور عليها في أي كتاب مدرسي تقريبًا عن التحليل الرياضي توسعات في الدوال الزوجية . بالإضافة إلى ذلك، فقد واجهتهم عدة مرات في ممارستي الشخصية:

مثال 6

يتم إعطاء الوظيفة. مطلوب:

1) قم بتوسيع الدالة إلى سلسلة فورييه مع النقطة، حيث يوجد رقم موجب تعسفي؛

2) اكتب التوسع في الفترة، وأنشئ دالة ورسمًا بيانيًا للمجموع الإجمالي للسلسلة.

حل: في الفقرة الأولى يقترح حل المشكلة بشكل عام، وهذا مريح للغاية! إذا دعت الحاجة، فقط استبدل القيمة الخاصة بك.

1) في هذه المشكلة تكون فترة التمدد نصف فترة. أثناء الإجراءات الإضافية، خاصة أثناء التكامل، يعتبر "el" ثابتًا

الدالة زوجية، مما يعني أنه يمكن توسيعها إلى سلسلة فورييه فقط في جيب التمام: .

نحن نبحث عن معاملات فورييه باستخدام الصيغ . انتبه إلى مزاياها غير المشروطة. أولاً، يتم التكامل على الجزء الإيجابي من التوسيع، مما يعني أننا نتخلص بأمان من الوحدة مع الأخذ في الاعتبار علامة "X" فقط للقطعتين. وثانيا، التكامل مبسط بشكل ملحوظ.

اثنين:

دعونا نتكامل بالأجزاء:

هكذا:
بينما الثابت الذي لا يعتمد على "en" يؤخذ خارج المجموع.

إجابة:

2) لنكتب التوسع في الفترة، وللقيام بذلك، نعوض بقيمة نصف الفترة المطلوبة في الصيغة العامة:

سلسلة فورييه من الدوال الدورية ذات الفترة 2π.

تسمح لنا متسلسلة فورييه بدراسة الدوال الدورية من خلال تحليلها إلى مكونات. تعد التيارات والفولتية المتناوبة والإزاحات وسرعة وتسارع آليات الكرنك والموجات الصوتية أمثلة عملية نموذجية لاستخدام الوظائف الدورية في الحسابات الهندسية.

يعتمد توسيع متسلسلة فورييه على افتراض أن جميع الدوال ذات الأهمية العملية في الفترة -π ≥x≥ π يمكن التعبير عنها في شكل متسلسلة مثلثية متقاربة (تعتبر السلسلة متقاربة إذا كانت تسلسل المجاميع الجزئية المكونة من حدودها يتقارب):

التدوين القياسي (= العادي) من خلال مجموع sinx وcosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

حيث a o, a 1,a 2,...,b 1,b 2,.. هي ثوابت حقيقية، أي.

حيث، بالنسبة للنطاق من -π إلى π، يتم حساب معاملات متسلسلة فورييه باستخدام الصيغ:

تسمى المعاملات a o و a n و b n معاملات فورييهوإذا أمكن العثور عليها، يتم استدعاء السلسلة (1). بجوار فورييه،المقابلة للوظيفة f(x). بالنسبة للمتسلسلة (1)، فإن المصطلح (a 1 cosx + b 1 sinx) يسمى الأول أو التوافقي الأساسي,

هناك طريقة أخرى لكتابة سلسلة وهي استخدام العلاقة acosx+bsinx=csin(x+α)

f(x)=أ o +c 1 خطيئة(x+α 1)+ج 2 خطيئة(2x+α 2)+...+c n خطيئة(nx+α n)

حيث a o ثابت، c 1 =(a 1 2 +b 1 2) 1/2، c n =(a n 2 +b n 2) 1/2 هي سعة المكونات المختلفة، ويساوي a n =arctg a n / ب ن.

بالنسبة للمتسلسلة (1)، فإن المصطلح (a 1 cosx+b 1 sinx) أو c 1 sin(x+α 1) يسمى الأول أو التوافقي الأساسي,(a 2 cos2x+b 2 sin2x) أو c 2 sin(2x+α 2) يسمى التوافقي الثانيوما إلى ذلك وهلم جرا.

يتطلب تمثيل إشارة معقدة بدقة عددًا لا نهائيًا من المصطلحات. ومع ذلك، في العديد من المشاكل العملية، يكفي النظر فقط في المصطلحات القليلة الأولى.

سلسلة فورييه من الدوال غير الدورية ذات الفترة 2π.

توسيع الوظائف غير الدورية.

إذا كانت الدالة f(x) غير دورية، فهذا يعني أنه لا يمكن توسيعها إلى سلسلة فورييه لجميع قيم x. ومع ذلك، فمن الممكن تعريف سلسلة فورييه التي تمثل دالة على أي نطاق بعرض 2π.

بالنظر إلى دالة غير دورية، يمكن إنشاء دالة جديدة عن طريق اختيار قيم f(x) ضمن نطاق معين وتكرارها خارج هذا النطاق بفواصل زمنية 2π. بما أن الدالة الجديدة دورية مع الفترة 2π، فيمكن توسيعها إلى سلسلة فورييه لجميع قيم x. على سبيل المثال، الدالة f(x)=x ليست دورية. ومع ذلك، إذا كان من الضروري توسيعها إلى سلسلة فورييه في الفترة من o إلى 2π، فسيتم إنشاء دالة دورية مع فترة 2π خارج هذه الفترة (كما هو موضح في الشكل أدناه).

بالنسبة للدوال غير الدورية مثل f(x)=x، فإن مجموع متسلسلة فورييه يساوي قيمة f(x) عند جميع النقاط في نطاق معين، ولكنه لا يساوي f(x) للنقاط خارج النطاق. للعثور على متسلسلة فورييه لدالة غير دورية في النطاق 2π، يتم استخدام نفس صيغة معاملات فورييه.

وظائف زوجية وغريبة.

يقولون الدالة y=f(x) حتى، إذا كانت f(-x)=f(x) لجميع قيم x. الرسوم البيانية للدوال الزوجية تكون دائمًا متناظرة حول المحور y (أي أنها صور معكوسة). مثالان للدوال الزوجية: y=x2 وy=cosx.

يقولون أن الدالة y=f(x) غريب،إذا كانت f(-x)=-f(x) لجميع قيم x. دائمًا ما تكون الرسوم البيانية للدوال الفردية متناظرة بالنسبة إلى الأصل.

العديد من الوظائف ليست زوجية ولا فردية.

توسيع سلسلة فورييه في جيب التمام.

تحتوي سلسلة فورييه للدالة الدورية الزوجية f(x) مع الفترة 2π على مصطلحات جيب التمام فقط (أي لا توجد مصطلحات جيبية) وقد تتضمن مصطلحًا ثابتًا. لذلك،

أين هي معاملات متسلسلة فورييه،

تحتوي سلسلة فورييه للدالة الدورية الفردية f(x) ذات الفترة 2π على مصطلحات ذات جيب التمام فقط (أي أنها لا تحتوي على مصطلحات ذات جيب التمام).

لذلك،

أين هي معاملات متسلسلة فورييه،

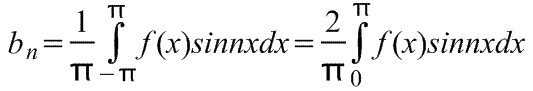
سلسلة فورييه في نصف دورة.

إذا تم تعريف دالة لنطاق، على سبيل المثال من 0 إلى π، وليس فقط من 0 إلى 2π، فيمكن توسيعها في سلسلة فقط في جيب التمام أو في جيب التمام فقط. وتسمى سلسلة فورييه الناتجة بالقرب من فورييه في نصف دورة.

إذا كنت ترغب في الحصول على التحلل نصف دورة فورييه بواسطة جيب التماموظائف f(x) في النطاق من 0 إلى π، فمن الضروري إنشاء دالة دورية زوجية. في التين. فيما يلي الدالة f(x)=x، المبنية على الفاصل الزمني من x=0 إلى x=π. بما أن الدالة الزوجية متناظرة حول المحور f(x)، فإننا نرسم الخط AB، كما هو موضح في الشكل. أقل. إذا افترضنا أنه خارج الفترة المدروسة، يكون الشكل الثلاثي الناتج دوريًا بفترة 2π، فإن الرسم البياني النهائي يبدو كما يلي: في التين. أقل. وبما أننا نحتاج إلى الحصول على توسع فورييه في جيب التمام، كما كان من قبل، فإننا نحسب معاملات فورييه a o و n

إذا كنت بحاجة للحصول على توسيع جيب فورييه نصف دورةوظائف f(x) في النطاق من 0 إلى π، فمن الضروري إنشاء دالة دورية فردية. في التين. فيما يلي الدالة f(x)=x، المبنية على الفاصل الزمني من x=0 إلى x=π. وبما أن الدالة الفردية متناظرة حول نقطة الأصل، فإننا نبني السطر CD، كما هو موضح في الشكل. إذا افترضنا أنه خارج الفاصل الزمني المدروس، تكون إشارة سن المنشار الناتجة دورية بفترة 2π، فإن الرسم البياني النهائي له الشكل الموضح في الشكل. وبما أننا نحتاج إلى الحصول على تمديد فورييه لنصف الدورة من حيث الجيوب، كما كان من قبل، فإننا نحسب معامل فورييه. ب

سلسلة فورييه لفترة تعسفية.

توسيع الدالة الدورية بالفترة L.

تتكرر الدالة الدورية f(x) مع زيادة x بمقدار L، أي. و(س+L)=و(خ). يعد الانتقال من الوظائف التي تم النظر فيها سابقًا بفترة 2π إلى وظائف ذات فترة L أمرًا بسيطًا للغاية، حيث يمكن إجراؤه باستخدام تغيير المتغير.

للعثور على متسلسلة فورييه للدالة f(x) في النطاق -L/2≤x≤L/2، نقدم متغيرًا جديدًا u بحيث تكون الدالة f(x) لها فترة 2π بالنسبة إلى u. إذا كانت u=2πx/L، فإن x=-L/2 لـ u=-π وx=L/2 لـ u=π. دع أيضًا f(x)=f(Lu/2π)=F(u). متسلسلة فورييه F(u) لها الشكل

(يمكن استبدال حدود التكامل بأي فترة طولها L مثلا من 0 إلى L)

سلسلة فورييه على نصف دورة للوظائف المحددة في الفاصل الزمني L≠2π.

بالنسبة للاستبدال u=πx/L، فإن الفاصل الزمني من x=0 إلى x=L يتوافق مع الفاصل الزمني من u=0 إلى u=π. وبالتالي، يمكن توسيع الدالة إلى سلسلة فقط في جيب التمام أو في الجيوب فقط، أي. الخامس سلسلة فورييه في نصف دورة.

توسيع جيب التمام في النطاق من 0 إلى L له النموذج

سلسلة فورييه من الدوال الدورية ذات الفترة 2π.

التدوين القياسي (= العادي) من خلال مجموع sinx وcosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

حيث a o, a 1,a 2,...,b 1,b 2,.. هي ثوابت حقيقية، أي.

حيث، بالنسبة للنطاق من -π إلى π، يتم حساب معاملات متسلسلة فورييه باستخدام الصيغ:

هناك طريقة أخرى لكتابة سلسلة وهي استخدام العلاقة acosx+bsinx=csin(x+α)

f(x)=أ o +c 1 خطيئة(x+α 1)+ج 2 خطيئة(2x+α 2)+...+c n خطيئة(nx+α n)

حيث a o ثابت، c 1 =(a 1 2 +b 1 2) 1/2، c n =(a n 2 +b n 2) 1/2 هي سعة المكونات المختلفة، ويساوي a n =arctg a n / ب ن.

سلسلة فورييه من الدوال غير الدورية ذات الفترة 2π.

توسيع الوظائف غير الدورية.

وظائف زوجية وغريبة.

العديد من الوظائف ليست زوجية ولا فردية.

توسيع سلسلة فورييه في جيب التمام.

أين هي معاملات متسلسلة فورييه،

لذلك،

أين هي معاملات متسلسلة فورييه،

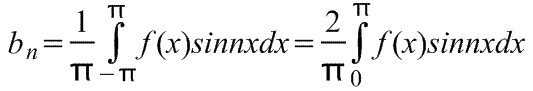
سلسلة فورييه في نصف دورة.

سلسلة فورييه لفترة تعسفية.

توسيع الدالة الدورية بالفترة L.

(يمكن استبدال حدود التكامل بأي فترة طولها L مثلا من 0 إلى L)

سلسلة فورييه على نصف دورة للوظائف المحددة في الفاصل الزمني L≠2π.

توسيع جيب التمام في النطاق من 0 إلى L له النموذج

تحتوي سلسلة فورييه للدالة الدورية الزوجية f(x) مع الفترة 2p فقط على مصطلحات ذات جيب التمام (أي لا تحتوي على مصطلحات ذات جيب) وقد تتضمن مصطلحًا ثابتًا. لذلك،

أين هي معاملات متسلسلة فورييه،

توسيع سلسلة فورييه في الجيوب

تحتوي سلسلة فورييه للدالة الدورية الفردية f (x) مع الفترة 2p على مصطلحات ذات جيب التمام فقط (أي أنها لا تحتوي على مصطلحات ذات جيب التمام).

لذلك،

أين هي معاملات متسلسلة فورييه،

سلسلة فورييه في نصف دورة

إذا تم تعريف دالة لنطاق، على سبيل المثال من 0 إلى p، وليس فقط من 0 إلى 2p، فيمكن توسيعها إلى سلسلة فقط في جيب التمام أو في جيب التمام فقط. وتسمى سلسلة فورييه الناتجة قريب فورييه على نصف دورة

إذا كنت ترغب في الحصول على التحلل فورييه على نصف دورة بواسطة جيب التماموظائف f (x) في النطاق من 0 إلى p، فمن الضروري بناء وظيفة دورية زوجية. في التين. فيما يلي الدالة f (x) = x، المبنية على الفاصل الزمني من x = 0 إلى x = p. بما أن الدالة الزوجية متناظرة حول المحور f (x)، فإننا نرسم الخط AB، كما هو موضح في الشكل. أقل. إذا افترضنا أنه خارج الفترة المدروسة، يكون الشكل الثلاثي الناتج دوريًا ودورته 2p، فإن الرسم البياني النهائي يبدو كما يلي: في التين. أقل. وبما أننا نحتاج إلى الحصول على توسع فورييه في جيب التمام، كما كان من قبل، فإننا نحسب معاملات فورييه a o و n

إذا كنت بحاجة للحصول على تقسيم فورييه على نصف دورة بواسطة الجيوب الأنفيةوظائف f (x) في النطاق من 0 إلى p، فمن الضروري إنشاء دالة دورية فردية. في التين. فيما يلي الدالة f (x) =x، المبنية على الفاصل الزمني من x=0 إلى x=p. وبما أن الدالة الفردية متناظرة حول نقطة الأصل، فإننا نبني السطر CD، كما هو موضح في الشكل.

إذا افترضنا أنه خارج الفاصل الزمني المدروس، تكون إشارة سن المنشار الناتجة دورية بفترة 2p، فإن الرسم البياني النهائي له الشكل الموضح في الشكل. وبما أننا نحتاج إلى الحصول على تمديد فورييه لنصف الدورة من حيث الجيوب، كما كان من قبل، فإننا نحسب معامل فورييه. ب

المجموع:0
في تواصل مع 0
جوجل+ 0
نعم 0
فيسبوك 0

منظر عام لسلسلة فورييه. الرياضيات العليا

توسيع الدالة إلى سلسلة فورييه على الفاصل الزمني

ما الذي يجب عليك فعله في المهام التالية؟

كيفية توسيع وظيفة إلى سلسلة فورييه؟

توسيع الدالة إلى سلسلة فورييه خلال فترة تعسفية

توسيع سلسلة فورييه للوظائف الزوجية والفردية

توسيع سلسلة فورييه في الجيوب

سلسلة فورييه في نصف دورة