ولكن بعد ذلك طُلب من الطالب إثبات أن مجموع زوايا المثلث يساوي 180 درجة. وأشار الطالب إلى خصائص الخطوط المتوازية. لكنه بدأ في إثبات خصائص الخطوط المتوازية على أساس علامات الخطوط المتوازية. الدائرة مغلقة. لذلك، عند تكرار النظرية، كن متسقًا ومنتبهًا. عند قراءة برهان نظرية ما، انتبه بشكل خاص إلى مكان استخدام شروط النظرية في البرهان وما هي النظريات التي تم إثباتها مسبقًا.
في هذا القسم، يتم تقديم صياغة النظريات وفقًا للكتاب المدرسي الذي ألفه A. V. Pogorelov "الهندسة. 7-9 درجات."
النظريات الأساسية للتخطيط وعواقبها
1. نظريات على المستقيمات (التوازي والتعامد على المستوى)
خصائص الخطوط المتوازية.خطان موازيان للثالث متوازيان (الشكل 57).
(أ||ج، ب||ج) ؟ أ||ب.
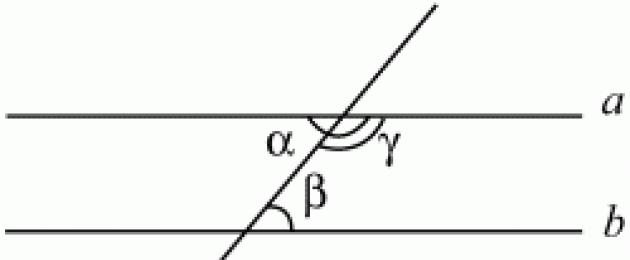
إذا تقاطع خطان متوازيان مع خط ثالث، فإن الزوايا العرضية الداخلية متساوية، ومجموع الزوايا الداخلية أحادية الجانب هو 180 درجة (الشكل 58).
أ||ب ؟ ؟ = ؟
؟ + ؟ = 180 درجة.

علامات الخطوط المتوازية.
إذا كان خطان مستقيمان يتقاطعان مع ثلث، وكانت الزوايا الداخلية المتقاطعة المتكونة متساوية، فإن الخطوط المستقيمة تكون متوازية (شكل 59):
هل الزوايا الداخلية المتقابلة متساوية؟ أ||ب.

إذا كان خطان مستقيمان يتقاطعان مع الثلث، وكان مجموع الزوايا الداخلية الناتجة من جانب واحد يساوي 180 درجة، فإن الخطوط المستقيمة متوازية (الشكل 60):
أ||ب.

إذا كان خطان مستقيمان يتقاطعان مع الثلث، وكانت الزوايا الناتجة متساوية، فإن الخطوط المستقيمة متوازية (الشكل 61):
أ||ب.

نظريات حول وجود وتفرد الخط العمودي. من خلال كل نقطة من الخط يمكنك رسم خط عمودي عليها، وواحد فقط (الشكل 62).

من أي نقطة لا تقع على خط معين، يمكنك خفض عمودي على هذا الخط، وواحد فقط (الشكل 63).

الخط b هو الخط الوحيد الذي يمر بالنقطة A المتعامدة مع النقطة a.
العلاقة بين التوازي والعمودي.
خطان متعامدان مع الخط الثالث متوازيان (الشكل 64).
(أ؟ ج، ب؟ ج) ؟ أ||ب.

إذا كان الخط عموديًا على أحد الخطين المتوازيين، فهو أيضًا عمودي على الآخر (الشكل 65):
(أ؟ ب، ب||ج) ؟ أ؟ مع.

أرز. 65.
2 نظريات حول الزوايا الزوايا في المثلث. الزوايا المدرجة في دائرة
خاصية الزوايا العمودية.الزوايا العمودية متساوية (الشكل 66):
? = ?.

خصائص زوايا المثلث متساوي الساقين. في المثلث المتساوي الساقين، زوايا القاعدة متساوية. النظرية العكسية صحيحة أيضًا: إذا كانت زاويتان في المثلث متساويتين، فهو متساوي الساقين (الشكل 67):
أ ب = ق؟ ?أ = ?ج.

نظرية مجموع زوايا المثلث.
مجموع الزوايا الداخلية للمثلث هو 180 درجة (الشكل 68):
؟ + ؟ + ؟ = 180 درجة.

نظرية مجموع الزوايا في n-gon المحدب.
مجموع زوايا n-gon المحدبة هو 180°(n – 2) (الشكل 69).

مثال: ?1 + ?2 + ?3 + ?4 + ?5 = 180°?(5–2) = 540°.
نظرية الزاوية الخارجية للمثلث.
الزاوية الخارجية للمثلث تساوي مجموع زاويتين داخليتين غير مجاورتين له (الشكل 70):
? = ? + ?.

نظرية قياس الزاوية المحيطية بالدائرة.
الزاوية المدرج في الدائرة تساوي نصف الزاوية المركزية المقابلة ف (الشكل 71):

أرز. 71.
3. النظريات الأساسية حول المثلثات
علامات تساوي المثلثات. إذا كان ضلعان والزاوية بينهما لمثلث واحد متساويان على التوالي مع ضلعين والزاوية بينهما لمثلث آخر، فإن هذه المثلثات متطابقة (الشكل 72).
ABC = ?A1B1C1 لأن AB = A1B1, AC = A1C1 و?A = ?A1.
إذا كانت الزوايا الجانبية والزوايا المجاورة لمثلث واحد متساوية، على التوالي، مع الجوانب والزوايا المجاورة لمثلث آخر، فإن هذه المثلثات متطابقة (الشكل 73).

ABC = ?A1B1C1 لأن AC = A1C1, ?A = ?A1, ?C = ?C1.
إذا كانت ثلاثة جوانب لمثلث واحد متساوية، على التوالي، مع ثلاثة جوانب لمثلث آخر، فإن هذه المثلثات متطابقة (الشكل 74).

ABC = ?A1B1C1 لأن AB = A1B1، AC = A1C1، BC = B1C1.
علامات المساواة في المثلثات القائمة.
إذا كان الوتر وساق أحد المثلثين متساويين على التوالي مع الوتر وساق مثلث آخر، فإن هذه المثلثات تكون متطابقة (الشكل 75).

ABC = ?A1B1C1 لأن ?A = ?A1 = 90°; قبل الميلاد = B1C1؛ أب = A1B1.
إذا كان الوتر والزاوية الحادة لمثلث واحد متساويين على التوالي مع الوتر والزاوية الحادة لمثلث آخر، فإن هذه المثلثات تكون متطابقة (الشكل 76).

ABC = ?A1B1C1, لأن AB = A1B1, ?A = ?A1 a ?C = ?C1 = 90°.
خاصية الوسيط للمثلث متساوي الساقين.
في المثلث المتساوي الساقين، الوسيط المرسوم على القاعدة هو المنصف والارتفاع (الشكل 77).

(AB = BC، AM = MS)؟ (؟AVM =؟MVS،؟AMV =؟BMC = 90°).
خاصية خط الوسط للمثلث.
الخط الأوسط للمثلث، الذي يصل بين منتصفي هذين الضلعين، يوازي الضلع الثالث ويساوي نصفه (الشكل 78).

EF||AC، EF = 1/2AC، نظرًا لأن AE = EB وBF = FC.
نظرية الجيب.
تتناسب جوانب المثلث مع جيب الزوايا المتقابلة (الشكل 79).

أرز. 79.

نظرية جيب التمام.
مربع أي جانب من أضلاع المثلث يساوي مجموع مربعي الضلعين الآخرين دون ضعف حاصل ضرب هذين الجانبين في جيب تمام الزاوية بينهما (الشكل 80).

A2= ب2+ ج2- 2ب ج كوس؟.
نظرية فيثاغورس (حالة خاصة من نظرية جيب التمام).
في المثلث القائم، يساوي مربع الوتر مجموع مربعات الأرجل (الشكل 81).

ج2= أ2+ ب2.
4. التناسب والتشابه على المستوى
نظرية طاليس.إذا قطعت الخطوط المتوازية المتقاطعة مع جوانب زاوية شرائح متساوية من أحد الجانبين، فإنها تقطع شرائح متساوية من الجانب الآخر (الشكل 82).

(AB = BC، AA1||BB1||CC1) ؟ A1B1 = В1С1، q و Р – الأشعة تشكل زاوية؟.
أ، ب، ج – الخطوط المستقيمة المتقاطعة مع جوانب الزاوية.
نظرية القطع التناسبية (تعميم نظرية طاليس).
الخطوط المستقيمة المتوازية التي تتقاطع مع جوانب الزاوية تقطع الأجزاء المتناسبة من جوانب الزاوية (الشكل 83).

أرز. 83.

أو

خاصية منصف المثلث.
منصف زاوية المثلث يقسم الضلع المقابل له إلى أجزاء متناسبة مع الجانبين الآخرين (الشكل 84).

لو؟ = ؟ إذن

أو

علامات تشابه المثلثات.
إذا كانت زاويتان لمثلث واحد تساوي زاويتين لمثلث آخر، فإن هذه المثلثات متشابهة (الشكل 85).

المثلثان ABC و A1B1C1 متشابهان؟ = ؟1 و؟ = ?1.
إذا كان ضلعان لمثلث واحد متناسبان مع ضلعين لمثلث آخر، وكانت الزوايا التي تشكلها هذه الأضلاع متساوية، فإن المثلثين متشابهان (الشكل 86).

المثلثان ABC و A1B1C1 متشابهان

و؟ = ?1.
إذا كانت جوانب مثلث واحد متناسبة مع جوانب مثلث آخر، فإن هذه المثلثات متشابهة (الشكل 87).

المثلثان ABC و A1B1C1 متشابهان

5. عدم المساواة الهندسية الأساسية
النسبة بين أطوال المستطيل المائل والمتعامد.إذا رسم خطان متعامدان ومائلان على خط مستقيم من نقطة واحدة، فإن أي خط مائل يكون أكبر من المتعامد، والخطوط المائلة المتساوية لها إسقاطات متساوية، ومن المائلتين تكون التي ذات الإسقاط الأكبر أكبر (الشكل 88):
أأ"< АВ < АС; если А"С >A"B، ثم AC > AB.

عدم المساواة المثلثية.
ومهما كانت النقاط الثلاث فإن المسافة بين أي نقطتين من هذه النقاط لا تزيد عن مجموع المسافات بينها وبين النقطة الثالثة. ويترتب على ذلك أنه في أي مثلث يكون كل ضلع أقل من مجموع الضلعين الآخرين (الشكل 89):
تكييف< АВ + ВС.

العلاقة بين مقاسات الأضلاع وقياسات الزوايا في المثلث.
في المثلث، يقع الضلع الأكبر مقابل الزاوية الأكبر، والزاوية الأكبر تقع مقابل الضلع الأكبر (الشكل 90).
(قبل الميلاد.< AB < AC) ? (?А < ?С < ?В).

أرز. 90.
6. المواقع الهندسية الأساسية للنقاط على المستوى
سيكون الموقع الهندسي لنقاط المستوى المتساوية البعد عن جوانب الزاوية هو منصف الزاوية المعطاة (الشكل 91).
AK = AT، حيث A هي أي نقطة على المنصف.
سيكون الموقع الهندسي للنقاط المتساوية البعد عن نقطتين معلومتين خطًا مستقيمًا متعامدًا مع القطعة التي تصل هذه النقاط وتمر بمنتصفها (شكل 92).

MA = MB، حيث M هي نقطة اختيارية على المنصف العمودي للقطعة AB.
سيكون الموقع الهندسي لنقاط المستوى المتساوية البعد عن نقطة معينة عبارة عن دائرة مركزها عند هذه النقطة (الشكل 93).

النقطة O متساوية البعد عن نقاط الدائرة.
موقع مركز الدائرة المحيطة بالمثلث.
مركز الدائرة المحيطة بالمثلث هو نقطة تقاطع الخطوط المتعامدة مع أضلاع المثلث المرسومة من خلال منتصف هذه الأضلاع (الشكل 94).

A، B، C هي رؤوس المثلث الواقع على الدائرة.
صباحا = MV و AK = كانساس.
النقطتان M وK هما أساسات الخطوط العمودية على الجانبين AB وAC، على التوالي.
موقع مركز الدائرة المرسومة في المثلث.
مركز الدائرة المدرج في المثلث هو نقطة تقاطع منصفاته (الشكل 95).

في ABC، القطع AT وSC منصفات.
7. نظريات حول الأشكال الرباعية
خصائص متوازي الأضلاع.متوازي الأضلاع له جوانب متقابلة متساوية. في متوازي الأضلاع، الزوايا المتقابلة متساوية.
تتقاطع أقطار متوازي الأضلاع وتنقسم إلى نصفين عند نقطة التقاطع (الشكل 96).

AB = CD، BC = AD، ?BAD = ?BCD, ?ABC = ?ADC, AO = OC, BO = OD.
علامات متوازي الأضلاع.
إذا كان الشكل الرباعي له ضلعان متوازيان ومتساويان، فهو متوازي أضلاع (شكل 97).

قبل الميلاد||م، قبل الميلاد = م؟ ABCD هو متوازي الأضلاع.
إذا تقاطعت أقطار الشكل الرباعي وانقسمت إلى نصفين عند نقطة التقاطع، فإن هذا الشكل الرباعي يكون متوازي أضلاع (الشكل 98).

AO = نظام التشغيل، VO = التطوير التنظيمي؟ ABCD هو متوازي الأضلاع.
خصائص المستطيل.
يحتوي المستطيل على جميع خصائص متوازي الأضلاع (المستطيل له أضلاع متقابلة متساوية، والمستطيل له زوايا متقابلة متساوية (90 درجة)، وأقطار المستطيل تتقاطع وتنقسم إلى نقطة التقاطع).
أقطار المستطيل متساوية (الشكل 99):
التيار المتردد = دينار بحريني.

علامة المستطيل.
إذا كان متوازي الأضلاع يحتوي على جميع الزوايا المتساوية، فهو مستطيل.
خصائص المعين.
يتميز المعين بجميع خصائص متوازي الأضلاع (المعين له جوانب متقابلة متساوية - بشكل عام، جميع الجوانب متساوية حسب التعريف؛ المعين له زوايا متقابلة متساوية؛ أقطار المعين تتقاطع وتنقسم إلى نصفين بواسطة التقاطع نقطة).
تتقاطع أقطار المعين بزوايا قائمة.
أقطار المعين هي منصفات زواياه (الشكل 100).

مكيف الهواء؟ BD، ?ABD = ?DBC = ?CDB = ?BDA, ?BAC = ?CAD = ?BCA = ?DCA.
علامة الماس.
إذا كان متوازي الأضلاع له أقطار متعامدة، فهو معين.
خصائص المربع.
المربع له خصائص المستطيل والمعين.
علامة مربعة.
إذا تقاطعت أقطار المستطيل بزاوية قائمة فهو مربع.
خاصية الخط الأوسط لشبه منحرف.
خط الوسط لشبه المنحرف موازي للقواعد ويساوي نصف مجموعها (الشكل 101).

أرز. 101.
معايير الرباعيات المنقوشة والمحدودة.
إذا كان من الممكن وصف دائرة حول شكل رباعي، فإن مجموع الزوايا المقابلة لها يساوي 180 درجة (الشكل 102).
أ + ج = ب + د = 180 درجة.

إذا أمكن رسم دائرة بشكل رباعي، فإن مجموع أضلاعها المتقابلة يكون متساويًا (الشكل 103).
أ ب + مؤتمر نزع السلاح = م + ق.

أرز. 103.
8. نظريات الدائرة
خاصية الحبال والقاطع.إذا تقاطع الأوتار AB و CD لدائرة عند النقطة S، إذن AS؟ بكالوريوس = CS؟ DS (الشكل 104).

إذا تم رسم قاطعين من النقطة S إلى دائرة، يتقاطعان مع الدائرة عند النقاط A، B و C، D، على التوالي، إذن AS ؟ بكالوريوس = CS؟ DS (الشكل 105).

رقم؟.
نسبة محيط الدائرة إلى قطرها لا تعتمد على نصف قطر الدائرة، أي أنها هي نفسها بالنسبة لأي دائرتين. هل هذا الرقم متساوي؟ (الشكل 106).


أرز. 106.
9. المتجهات
نظرية تحلل المتجه بالنسبة للأساس.إذا تم إعطاء متجهين غير خطيين a وb وأي متجه آخر c على المستوى، فهناك أرقام فريدة n وm بحيث c = na + mb (الشكل 107).
أين


نظرية المنتج العددي للمتجهات.
المنتج العددي للمتجهات يساوي منتج قيم q المطلقة (الأطوال) بواسطة جيب تمام الزاوية بينهما (الشكل 108).
الزراعة العضوية؟ OB = الزراعة العضوية؟ أو بي؟ كوس؟

أرز. 108.
الصيغ الأساسية للقياس
بالنسبة للمثلث (الشكل 109):
أرز. 109.

حيث a، b، c هي أضلاع المثلث؛
?, ?, ? - الزوايا المقابلة لهم؛
r و R هما نصف قطر الدوائر المنقوشة والمحدودة؛
ha، ma، la - الارتفاع والوسيط والمنصف المرسوم على الجانب أ؛
S - مساحة المثلث؛

- نصف محيط المثلث .
يتم تقسيم المتوسطات في المثلث على نقطة التقاطع بنسبة 2:1، اعتبارًا من الرأس (الشكل 110).

أرز. 110.

بالنسبة للأشكال الرباعية:

حيث a، b هي أطوال القواعد؛
ح - ارتفاع شبه المنحرف.
مساحة متوازي الأضلاع مع الجوانب أ، ب والزاوية؟ بينهما يتم حسابها بالصيغة S = ab sin ؟. يمكنك أيضًا استخدام الصيغة:

حيث d1, d2 هي أطوال الأقطار؟ - الزاوية بينهما (أو S = aha، حيث ha هو الارتفاع).
بالنسبة للشكل الرباعي المحدب التعسفي (الشكل 111):


بالنسبة إلى n-gon العادي:

(R و r هما نصف قطر الدوائر المقيدة والمدرجة، وan هو طول ضلع n-gon المنتظم).
بالنسبة للدائرة والدائرة (الشكل 112):

أرز. 112.

و1\2R2؟، إذا؟ أعرب في راديان.
الجزء = القطاع - المثلث.
الصيغ التحليلية للتخطيط
إذا كانت النقطتان A(x1; y1) و B(x2; y2) معطاتين، إذنمعادلة الخط AB:

يمكن اختصاره بسهولة إلى الشكل ax + by + c = 0، حيث يكون المتجه n = (a, b) متعامدًا مع الخط.
المسافة من النقطة A(x1; y1) إلى الخط المستقيم ax + by + c = 0 هي

المسافة بين الخطوط المتوازية ax + by + c1 = 0 و ax + by + c2 = 0 هي

يتم حساب الزاوية بين الخطوط المستقيمة a1x + BLу + c1 = 0 و a2x + b2y + c2 = 0 بالصيغة:

معادلة دائرة مركزها النقطة O(x0, y0) ونصف قطرها R:(x – xo)2+ (y – yo)2= R2.
3.2. أسئلة الاختبار الذاتي
1. أ) ما هي خصائص الزوايا الرأسية التي تعرفها؟ (1)
2. أ) صياغة معيار لتساوي المثلثات على طول الجانبين والزاوية بينهما. (1)
3. أ) صياغة معيار لتساوي المثلثات على طول الجانب والزاويتين. (1)
ب) أثبت هذه العلامة. (1)
4. أ) اذكر الخصائص الرئيسية للمثلث متساوي الساقين. (1)
ج) إثبات اختبار المثلث متساوي الساقين. (1)
5. أ) صياغة معيار لتساوي المثلثات من ثلاثة جوانب. (1)
ب) أثبت هذه العلامة. (1)
6. أثبت أن الخطين الموازيين للثالث متوازيان. (2)
7. أ) صياغة علامات توازي الخطوط. (1)
ج) إثبات النظريات العكسية. (1)
8. إثبات نظرية مجموع زوايا المثلث. (1)
9. أثبت أن الزاوية الخارجية للمثلث تساوي مجموع زاويتين داخليتين غير مجاورتين له. (1)
10. أ) صياغة معايير تساوي المثلثات القائمة. (1)
ب) إثبات معايير تساوي المثلثات القائمة على طول الوتر والساق؛ على طول الوتر والزاوية الحادة. (1)
11. أ) أثبت أنه من نقطة لا تقع على خط معين، يمكن إسقاط عمود واحد على هذا الخط. (1)
ب) أثبت أنه من خلال نقطة تقع على خط معين يمكن رسم خط فريد وعمودي على الخط المعطى. (1)
12. أ) أين يقع مركز الدائرة المحيطة بالمثلث؟ (1)
13. أ) أين يقع مركز الدائرة المحيطية في المثلث؟ (1)
ب) إثبات النظرية المقابلة. (1)
14. إثبات خاصية مماس الدائرة. (1)
15. أ) ما هي خصائص متوازي الأضلاع التي تعرفها؟ (1)
ب) إثبات هذه الخصائص. (1)
16. أ) ما هي علامات متوازي الأضلاع التي تعرفها؟ (1)
ب) إثبات هذه العلامات. (1)
17. أ) ما هي خصائص وخصائص المستطيل التي تعرفها؟ (1)
18. أ) ما هي خصائص وعلامات المعين التي تعرفها؟ (1)
ب) إثبات هذه الخصائص والعلامات. (1)
19. أ) ما هي خصائص وعلامات المربع التي تعرفها؟ (1)
ب) إثبات هذه الخصائص والعلامات. (1)
20. أ) اذكر نظرية طاليس. (1)
ب) أثبت هذه النظرية. (1)
21. أ) صياغة نظرية طاليس المعممة (نظرية القطع المتناسبة). (1)
ب) أثبت هذه النظرية. (2)
22. أ) ما هي خصائص الخط الأوسط للمثلث التي تعرفها؟ (1)
ب) إثبات هذه الخصائص. (1)
23. أ) ما هي الخصائص التي تعرفها للخط الأوسط لشبه المنحرف؟ (1)
ب) إثبات هذه الخصائص. (1)
24. أ) اذكر نظرية فيثاغورس. (1)
ب) إثبات نظرية فيثاغورس. (1)
ج) صياغة وإثبات نظرية العكس. (2)
25. أثبت أن أي مائل أكبر من المتعامد، وأن المائلتين المائلتين أكبر منهما. (1)
26. أ) صياغة عدم المساواة المثلث. (1)
ب) إثبات عدم المساواة المثلث. (2)
27. تم إعطاء إحداثيات النقطتين A(x1; y1) و B(x2; y2).
أ) ما الصيغة المستخدمة لحساب طول القطعة AB؟ (1)
ب) اشتق هذه الصيغة. (1)
28. اشتق معادلة دائرة مركزها النقطة A(x0; y0) ونصف قطرها R. (1)
29. أثبت أن أي خط في الإحداثيات الديكارتية x,y له معادلة على الشكل ax + by + c = 0. (2)
30. اكتب معادلة الخط المستقيم الذي يمر بالنقطتين A(x1; y1) و B(x2; y2). الجواب: تبرير ذلك. (2)
31. أثبت أنه في معادلة الخط المستقيم y = kx + b، الرقم k هو ظل زاوية ميل الخط المستقيم إلى الاتجاه الموجب لمحور x. (2)
32. أ) ما هي الخصائص الأساسية للحركات التي تعرفها؟ (2)
ب) إثبات هذه الخصائص. (3)
33. أثبت أن:
أ) تحويل التماثل حول نقطة ما هو حركة؛ (3)
ب) تحويل التماثل حول خط مستقيم هو حركة؛ (3)
ج) الترجمة الموازية هي الحركة. (3)
34. إثبات نظرية وجود وتفرد النقل الموازي. (3)
35. أثبت أن القيمة المطلقة للمتجه ka تساوي |k| ؟ |a|، بينما اتجاه المتجه ka عند a؟ O يتزامن مع اتجاه المتجه a if k > 0، وعكس اتجاه المتجه a if k< 0. (1)
36. أثبت أن أي متجه a يمكن توسيعه إلى المتجهين b وc (جميع المتجهات الثلاثة تقع على نفس المستوى). (1)
37. بالنظر إلى المتجهات a = (a1; a2) وb = (BL; b2). اثبت ذلك
![]()
أين؟ - الزاوية بين المتجهات.
38. أ) ما هي الخصائص التي تعرفها عن المنتج القياسي للمتجهات؟ (1)
ب) إثبات هذه الخصائص. (2)
39. إثبات أن التجانس هو تحويل التشابه. (1)
40. أ) ما هي خصائص تحويل التشابه التي تعرفها؟ (1)
ب) أثبت أن تحويل التشابه يحفظ الزوايا بين الأشعة. (2)
41. أ) صياغة اختبار لتشابه المثلثات في زاويتين. (1)
42. أ) صياغة معيار لتشابه المثلثات على أساس الجانبين والزاوية بينهما. (1)
ب) أثبت هذه العلامة. (1)
43. أ) صياغة معيار لتشابه المثلثات من ثلاثة جوانب. (1)
ب) أثبت هذه العلامة. (2)
44. أ) اذكر خاصية منصف المثلث. (1)
ب) أثبت أن منصف المثلث يقسم الضلع المقابل إلى قطع تتناسب مع الضلعين الآخرين. (1)
45. أ) اذكر خاصية الزاوية المحيطية داخل الدائرة. (1)
ب) إثبات هذه الخاصية. (1)
46. أ) أثبت أنه إذا تقاطع الأوتار AB و CD لدائرة عند النقطة S، فإن AS؟ بكالوريوس = CS؟ د.س. (1)
ب) أثبت أنه إذا تم رسم قاطعين من النقطة S إلى دائرة، يتقاطعان مع الدائرة عند النقاط A، B و C، D، على التوالي، فإن AS ؟ بكالوريوس = CS؟ د.س. (1)
47. أ) اذكر نظرية جيب التمام للمثلث. (1)
ب) أثبت هذه النظرية. (1)
48. أ) اذكر نظرية الجيب. (1)
ب) أثبت هذه النظرية. (1)
ج) أثبت أنه في نظرية الجيب لكل من العلاقات الثلاث:

يساوي 2R، حيث R هو نصف قطر الدائرة المحيطة بالمثلث. (1)
49. أثبت أنه في المثلث، الزاوية الأكبر تقع مقابل الضلع الأكبر، والضلع الأكبر يقع مقابل الزاوية الأكبر. (2)
50. أ) ما هو مجموع زوايا n-gon المحدبة؟ (1)
ب) اشتق صيغة مجموع زوايا المضلع n المحدب. (1)
51. أ) إثبات أنه يمكن كتابة دائرة في مضلع منتظم. (1)
ب) أثبت أنه يمكن تحديد الدائرة حول مضلع منتظم. (1)
52. معطى n منتظم مع الجانب أ. اشتقاق الصيغ:
أ) أنصاف أقطار الدوائر المنقوشة والمحدودة؛ (1)
ب) مساحة n-gon؛ (1)
ج) زاوية الرأس. (1)
53. أثبت أن نسبة محيط الدائرة إلى قطرها لا تعتمد على حجم الدائرة. (3)
54. كيفية تحويل الزوايا من الدرجات إلى الراديان والعكس؟ (1)
55. أثبت أن مساحة المستطيل تساوي حاصل ضرب طول المستطيل وعرضه. (3)
56. أ) ما هي الصيغة المستخدمة لحساب مساحة متوازي الأضلاع؟ (1)
ب) اشتق هذه الصيغة. (1)
57. أ) ما هي الصيغة المستخدمة لحساب مساحة المثلث؟ (من خلال القاعدة والارتفاع). (1)
ب) اشتق هذه الصيغة. (1)
ج) اشتق صيغة هيرون. (1)
58. أ) ما هي الصيغة المستخدمة لحساب مساحة شبه المنحرف؟ (1)
ب) اشتق هذه الصيغة. (1)
59. اشتقاق الصيغ:

حيث a، b، c هي أطوال أضلاع المثلث؛
س – مساحتها؛
R و r هما نصف قطر الدوائر المقيدة والمدرجة. (1)
60. اجعل F1 و F2 رقمين متشابهين مع معامل التشابه k. كيف ترتبط مجالات هذه الأرقام؟ الجواب: تبرير ذلك. (1)
61. أ) ما هي الصيغة المستخدمة لحساب مساحة الدائرة؟ (1)
ب) اشتق هذه الصيغة. (3)
62. اشتقاق صيغة مساحة القطاع الدائري. (2)
63. اشتقاق صيغة مساحة القطعة الدائرية. (2)
64. أ) أثبت أن منصفات المثلث تتقاطع عند نقطة واحدة. (2)
ب) أثبت أن متوسطات المثلث تتقاطع عند نقطة واحدة. (2)
ج) إثبات أن ارتفاعات المثلث (أو امتداداتها) تتقاطع عند نقطة واحدة. (2)
د) أثبت أن المنصفات المتعامدة على أضلاع المثلث تتقاطع عند نقطة واحدة. (1)
65. أثبت أن مساحة المثلث تساوي نصف حاصل ضرب ضلعيه وجيب الزاوية بينهما. (1)
66. أ) نظرية الدولة سيفا. (3)
ب) أثبت هذه النظرية. (3)
67. أ) نظرية الدولة مينلاي. (3)
ب) أثبت هذه النظرية. (3)
ج) صياغة وإثبات نظرية العكس. (3)
68. أ) أثبت أنه إذا كانت أضلاع إحدى الزوايا متوازية مع أضلاع زاوية أخرى، فإن هذه الزوايا إما أن تكون متساوية أو 180 درجة. (2)
في البداية، دعونا نشير إلى العديد من الخصائص الأساسية لأنواع مختلفة من الزوايا:
- مجموع الزوايا المجاورة يصل إلى 180 درجة.
- الزوايا العمودية متساوية مع بعضها البعض.
الآن دعنا ننتقل إلى خصائص المثلث. يجب أن يكون هناك مثلث تعسفي:
ثم، مجموع زوايا المثلث:
تذكر ذلك أيضًا مجموع أي ضلعين في المثلث يكون دائمًا أكبر من الضلع الثالث. مساحة المثلث المقاسة بضلعين والزاوية بينهما:
![]()
مساحة المثلث من خلال الجانب والارتفاع الذي انخفض عليه:
يمكن إيجاد نصف محيط المثلث بالصيغة التالية:
![]()
صيغة هيرونلمساحة المثلث :
مساحة المثلث من حيث محيط نصف القطر:
صيغة الوسيط (الوسيط هو خط مرسوم عبر قمة معينة ومنتصف الجانب الآخر في المثلث):

خصائص الوسيطات:
- تتقاطع المتوسطات الثلاثة عند نقطة واحدة.
- المتوسطات تقسم المثلث إلى ستة مثلثات متساوية المساحة.
- عند نقطة التقاطع، يتم تقسيم المتوسطات بنسبة 2:1، بدءًا من القمم.
خاصية المنصف (المنصف هو الخط الذي يقسم زاوية معينة إلى زاويتين متساويتين، أي إلى النصف):

من المهم أن تعرف: يقع مركز الدائرة المرسومة في المثلث عند تقاطع المنصفين(تتقاطع المنصفات الثلاثة عند هذه النقطة الواحدة). صيغ المنصف:
![]()

الخاصية الرئيسية لارتفاعات المثلث (الارتفاع في المثلث هو خط يمر عبر بعض رؤوس المثلث المتعامدة مع الجانب الآخر):
تتقاطع الارتفاعات الثلاثة في المثلث عند نقطة واحدة. يتم تحديد موضع نقطة التقاطع حسب نوع المثلث:
- إذا كان المثلث حادا فإن نقطة تقاطع الارتفاعات تكون داخل المثلث.
- في المثلث القائم، تتقاطع الارتفاعات عند رأس الزاوية القائمة.
- إذا كان المثلث منفرجا فإن نقطة تقاطع الارتفاعات تكون خارج المثلث.

خاصية أخرى مفيدة لارتفاعات المثلث:

نظرية جيب التمام:
نظرية الجيب:

يقع مركز الدائرة التي يحدها مثلث عند تقاطع عمودي المنصفين.تتقاطع المنصفات المتعامدة الثلاثة عند هذه النقطة الواحدة. المنصف العمودي - الخط المرسوم من منتصف ضلع المثلث المتعامد عليه.
نصف قطر الدائرة المدرج في مثلث منتظم:
نصف قطر الدائرة المحيطة بمثلث متساوي الأضلاع:
مساحة المثلث المنتظم:
نظرية فيثاغورسللمثلث القائم ( ج- الوتر، أو ب- الساقين):
نصف قطر الدائرة المدرج في مثلث قائم الزاوية:
![]()
نصف قطر الدائرة المحاطة بمثلث قائم الزاوية:
مساحة المثلث القائم ( ح- الارتفاع منخفضًا إلى الوتر):
![]()
خصائص الارتفاع المخفض إلى الوتر في المثلث القائم الزاوية:

مثلثات متشابهة- المثلثات التي تكون زواياها متساوية على التوالي، وتتناسب أضلاع إحداها مع أضلاع الأخرى المتشابهة. في المثلثات المتشابهة، تكون الخطوط المتناظرة (الارتفاعات والمتوسطات والمنصفات وما إلى ذلك) متناسبة. جوانب مماثلةمثلثات متشابهة - أضلاعها متقابلة بزوايا متساوية. معامل التشابه- رقم ك، تساوي نسبة الأضلاع المتشابهة لمثلثات متشابهة. النسبة بين محيطات المثلثات المتشابهة تساوي معامل التشابه. النسبة بين أطوال المنصفات والمتوسطات والارتفاعات والمنصفات المتعامدة تساوي معامل التشابه. النسبة بين مساحات المثلثات المتشابهة تساوي مربع معامل التشابه. علامات تشابه المثلثات:
- على زاويتين. إذا كانت زاويتان في مثلث متساويتين على التوالي زاويتين في مثلث آخر، فإن المثلثين متشابهان.
- على الجانبين والزاوية بينهما. إذا كان ضلعان في مثلث متناسبين مع ضلعين في آخر، وكانت الزوايا بين هذين الضلعين متساوية، فإن المثلثين متشابهان.
- على ثلاث جهات. إذا كانت ثلاثة أضلاع لمثلث واحد متناسبة مع ثلاثة أضلاع متشابهة في مثلث آخر، فإن المثلثين متشابهان.
شبه منحرف
شبه منحرف- شكل رباعي به زوج واحد من الأضلاع المتقابلة المتوازية. طول خط الوسط شبه المنحرف:
منطقة شبه منحرف:

بعض خصائص شبه المنحرف:
- الخط الأوسط لشبه المنحرف موازي للقواعد.
- القطعة التي تربط منتصف أقطار شبه المنحرف تساوي نصف الفرق بين القاعدتين.
- في شبه المنحرف، تكون نقاط منتصف القاعدتين ونقطة تقاطع الأقطار ونقطة تقاطع امتدادات الجوانب الجانبية على نفس الخط المستقيم.
- أقطار شبه المنحرف تقسمه إلى أربعة مثلثات. المثلثات التي أضلاعها قاعدتاها متشابهة، والمثلثات التي أضلاعها أضلاعها متشابهة.
- إذا كان مجموع زوايا أي قاعدة في شبه منحرف يساوي 90 درجة، فإن القطعة التي تربط منتصف القاعدتين تساوي نصف الفرق بين القاعدتين.
- شبه منحرف متساوي الساقين له زوايا متساوية عند أي قاعدة.
- شبه منحرف متساوي الساقين له أقطار متساوية.
- في شبه المنحرف متساوي الساقين، يقسم الارتفاع المنخفض من الرأس إلى القاعدة الأكبر إلى قسمين، أحدهما يساوي نصف مجموع القاعدتين، والآخر يساوي نصف الفرق بين القاعدتين.
متوازي الاضلاع
متوازي الاضلاعهو شكل رباعي أضلاعه المتقابلة متوازية في أزواج، أي أنها تقع على خطوط متوازية. مساحة متوازي الأضلاع من خلال الجانب والارتفاع المخفض عليه:
مساحة متوازي الأضلاع من خلال الجانبين والزاوية بينهما:
![]()
بعض خصائص متوازي الأضلاع:
- الأضلاع المتقابلة في متوازي الأضلاع متساوية.
- الزوايا المتقابلة في متوازي الأضلاع متساوية.
- أقطار متوازي الأضلاع تتقاطع وتنقسم عند نقطة التقاطع.
- مجموع الزوايا المجاورة لأحد الجانبين هو 180 درجة.
- مجموع زوايا متوازي الأضلاع هو 360 درجة.
- مجموع مربعات أقطار متوازي الأضلاع يساوي ضعف مجموع مربعات أضلاعه.
مربع
مربع- شكل رباعي جميع أضلاعه متساوية وقياس زواياه 90 درجة. مساحة المربع من حيث طول ضلعه:
مساحة المربع من حيث طول قطره:
خصائص المربع- هذه كلها خصائص متوازي الأضلاع والمعين والمستطيل في نفس الوقت.
الماس والمستطيل
المعينهو متوازي الأضلاع حيث جميع الجوانب متساوية. مساحة المعين (الصيغة الأولى تكون من خلال قطرين، والثانية من خلال طول الضلع والزاوية بين الجانبين):
![]()
خصائص المعين:
- المعين هو متوازي الأضلاع. ضلعاه المتقابلان متوازيان في أزواج.
- تتقاطع أقطار المعين بزاوية قائمة وتنقسم إلى نصفين عند نقطة التقاطع.
- أقطار المعين هي منصفات زواياه.
مستطيلهو متوازي أضلاع تكون فيه جميع الزوايا قائمة (تساوي 90 درجة). مساحة المستطيل من خلال ضلعين متجاورين:
خصائص المستطيل:
- قطرا المستطيل متساويان.
- المستطيل هو متوازي أضلاع - ضلعاه المتقابلان متوازيان.
- أضلاع المستطيل هي أيضًا ارتفاعاته.
- مربع قطر المستطيل يساوي مجموع مربعي ضلعيه غير المتقابلين (حسب نظرية فيثاغورس).
- يمكن تحديد دائرة حول أي مستطيل، وقطر المستطيل يساوي قطر الدائرة المحصورة.
مذكرة توضيحية
التذاكر المعروضة مخصصة للشفهية نظرينقل الامتحان السنوي عن طريق التخطيط الطلاب في الصف التاسع من المدرسة الأساسية، وكذلك في الصفين العاشر والحادي عشر من أجل التحضير لامتحان الدولة الموحدة. المواد المقدمة متوافقة تماماً مع برنامج الرياضيات وبرنامج التدريب المتخصص.
تتكون التذاكر من عشرة أسئلة تعكس الاتجاهات الرئيسية لمقرر الهندسة.
تهدف الأسئلة إلى اختبار إتقان الجهاز المفاهيمي للموضوع وتحديد مستوى المعرفة بالحقائق النظرية المهمة. ويشترط بعضها إثباتًا للمادة المقدمة، مع إظهار المعرفة بالمبادئ النظرية الأساسية للدورة والقدرة على تبريرها.
هذه الأسئلة مأخوذة من الأدلة:
الهندسة. مشاكل الإثبات. سميرنوف في إيه، سميرنوفا آي إم.
الهندسة. كتاب مدرسي للصفوف 7-9. أتاناسيان، بوتوزوف، كادومتسيف وآخرون.
الهندسة. كتاب مدرسي للصفوف 7-11.
معايير تقييم إجابات الطلاب
عند تقييم استجابات الطلاب، يمكنك استخدام المعايير التالية.
للحصول على إجابة كاملة وصحيحة لجميع الأسئلة على التذكرة، يتم إعطاء درجة "5". للحصول على درجة "3" يكفي الإجابة على ثمانية أسئلة على التذكرة.
وفي جميع الحالات الأخرى تكون النتيجة "4".
اختبار في قياس المساحة
الخيار 1
علامات تساوي المثلثات.
خاصية خط الوسط للمثلث.
تحديد ارتفاع المثلث.
ما أنصاف أقطار الدوائر المحيطية والمحددة في المثلث القائم؟
خصائص الشخصيات المماثلة.
كيف يتم قياس الزاوية المركزية؟
خاصية الأوتار في الدائرة.
مركز الدائرة المحيطة بالمثلث القائم الزاوية.
خاصية المثلث القائم الزاوية الحادة التي قياسها 30 درجة.
تحديد المنصف العمودي.
الخيار 2
علامات المساواة في المثلثات القائمة.
تحديد متوسط المثلث.
نظرية فيثاغورس.
ما هو مجموع مربعات الأقطار في متوازي الأضلاع؟
صيغة لمنطقة المثلث المنتظم.
مساحة شبه منحرف.
خاصية الزوايا المحيطية.
خاصية الشكل الرباعي المحدود.
طول القوس.
جيب التمام، جيب التمام، ظل زاوية 30 درجة.
الخيار 3
نظرية مجموع زوايا المثلث.
خصائص متوسطات المثلث.
تحديد منصف المثلث.
نظرية جيب التمام.
صيغة منصف المثلث.
مساحة متوازي الأضلاع (3).
ما هي الزاوية المحصورة بين قاطعين يتقاطعان خارج الدائرة؟
خاصية الشكل الرباعي المنقوش.
محيط.
الخصائص الأساسية للأوتار.
الخيار 4
خصائص المثلث متساوي الساقين.
خاصية المنصفات المتعامدة.
صيغة لمتوسطات المثلث.
نظرية الجيب.
ما هي قيم العناصر في المثلث متساوي الأضلاع (الارتفاع، نصف القطر، المساحة)؟
خصائص شبه منحرف متساوي الساقين.
خاصية خطوط المماس والقاطع الصادرة من نفس النقطة.
ما هي الزاوية بين الحبال المتقاطعة؟
جيب التمام، جيب التمام، ظل زاوية 60 درجة.
أين يقع مركز الدائرة المحيطية في المثلث؟
الخيار 5
عدم المساواة المثلثية.
نظرية ارتفاعات المثلث.
مساحات المثلثات المتشابهة.
صيغ مناطق المثلث (6).
علامات متوازي الأضلاع.
نظرية حول خط الوسط شبه المنحرف.
صيغة هيرون للشكل الرباعي.
ما هي الزاوية المحصورة بين المماس والوتر المرسوم من نقطة التماس؟
منطقة القطاع.
جيب التمام، جيب التمام، ظل زاوية 45 درجة.
الخيار 6
تحديد خط الوسط للمثلث.
نظرية منصف المثلث.
علامات تشابه المثلثات.
نظرية جيب التمام.
صيغة هيرون.
خصائص متوازي الأضلاع.
مساحة المعين.
مركز الدائرة المنقوشة والمحدودة في المثلث.
تحديد الجيب وجيب التمام والظل وظل التمام للزاوية الحادة للمثلث القائم
تتضمن دورة الفيديو "احصل على A" جميع المواضيع اللازمة لاجتياز اختبار الدولة الموحدة في الرياضيات بنجاح مع 60-65 نقطة. أكمل جميع المهام من 1 إلى 13 من امتحان الدولة الموحدة للملف التعريفي في الرياضيات. مناسب أيضًا لاجتياز امتحان الدولة الموحدة الأساسي في الرياضيات. إذا كنت ترغب في اجتياز امتحان الدولة الموحدة برصيد 90-100 نقطة، فأنت بحاجة إلى حل الجزء الأول في 30 دقيقة وبدون أخطاء!
دورة تحضيرية لامتحان الدولة الموحدة للصفوف 10-11 وكذلك للمعلمين. كل ما تحتاجه لحل الجزء الأول من امتحان الدولة الموحدة في الرياضيات (أول 12 مسألة) والمسألة 13 (علم المثلثات). وهذا أكثر من 70 نقطة في امتحان الدولة الموحدة، ولا يستطيع طالب 100 نقطة ولا طالب العلوم الإنسانية الاستغناء عنها.
كل النظرية اللازمة. الحلول السريعة والمزالق وأسرار امتحان الدولة الموحدة. تم تحليل جميع المهام الحالية للجزء الأول من بنك مهام FIPI. تتوافق الدورة تمامًا مع متطلبات امتحان الدولة الموحدة 2018.
تحتوي الدورة على 5 مواضيع كبيرة، مدة كل منها 2.5 ساعة. يتم تقديم كل موضوع من الصفر، ببساطة ووضوح.
المئات من مهام امتحان الدولة الموحدة. المسائل اللفظية ونظرية الاحتمالات. خوارزميات بسيطة وسهلة التذكر لحل المشكلات. الهندسة. النظرية والمواد المرجعية وتحليل جميع أنواع مهام امتحان الدولة الموحدة. القياس المجسم. حلول صعبة، أوراق غش مفيدة، تطوير الخيال المكاني. علم المثلثات من الصفر إلى المشكلة 13. الفهم بدلاً من الحشر. تفسيرات واضحة للمفاهيم المعقدة. الجبر. الجذور والقوى واللوغاريتمات والدالة والمشتقات. أساس لحل المشكلات المعقدة للجزء الثاني من امتحان الدولة الموحدة.