الجانبان المتقابلان من الشكل الرباعي المحدود. الصيغ ذات الأقطار

مادة من ويكيبيديا – الموسوعة الحرة

في الهندسة الإقليدية، رباعي مكتوبهو شكل رباعي تقع رءوسه جميعها على نفس الدائرة. تسمى هذه الدائرة دائرة مقيدةشكل رباعي، وقيل إن رؤوسه تقع على نفس الدائرة. يسمى مركز هذه الدائرة ونصف قطرها على التوالي مركزو نصف القطردائرة مقيدة. مصطلحات أخرى لهذا الرباعي: الشكل الرباعي يقع على دائرة واحدة، أضلاع الشكل الرباعي الأخير هي أوتار الدائرة. عادةً ما يُفترض أن الشكل الرباعي المحدب هو شكل رباعي محدب. الصيغ والخصائص الواردة أدناه صالحة في الحالة المحدبة.
يقولون أنه إذا يمكن رسم دائرة حول شكل رباعي، الذي - التي الشكل الرباعي مكتوب في هذه الدائرة، والعكس صحيح.

المعايير العامة لتسجيل الشكل الرباعي

حول شكل رباعي محدب $\باي$ راديان) أي:

\الزاوية A+\الزاوية C = \الزاوية B + \الزاوية D = 180^\circ

أو في ملاحظة الشكل:

$\alpha + \gamma = \beta + \delta = \pi = 180^(\circ).$

من الممكن وصف دائرة حول أي شكل رباعي تتقاطع فيه منصفات أضلاعه الأربعة عند نقطة واحدة (أو وساطات أضلاعه، أي متعامدة الأضلاع التي تمر بمنتصفها).
يمكنك وصف دائرة حول أي شكل رباعي له زاوية خارجية واحدة مجاورة له نظرا للزاوية الداخلية، تساوي تمامًا الزاوية الداخلية المقابلة لها نظرا للزاوية الداخلية. في جوهرها، هذه الحالة هي حالة عدم التوازي لجانبين متقابلين من الشكل الرباعي. في التين. يوجد أدناه الزوايا الخارجية والداخلية المجاورة للمضلع الخماسي الأخضر.

\displaystyle AX\cdot XC = BX\cdot XD.

تداخل Xقد تكون داخلية أو خارجية للدائرة. في الحالة الأولى، نحصل على الشكل الرباعي الدائري ا ب ت ث، وفي الحالة الأخيرة نحصل على شكل رباعي منقوش اي بي دي سي. عند التقاطع داخل دائرة فإن المساواة تنص على حاصل ضرب أطوال القطع التي تقع فيها النقطة Xيقسم قطريًا واحدًا، ويساوي حاصل ضرب أطوال الأجزاء التي تقع فيها النقطة Xيقسم قطري آخر. تُعرف هذه الحالة باسم "نظرية الوتر المتقاطع". في حالتنا، أقطار الشكل الرباعي المنقوش هي أوتار الدائرة.
معيار آخر للإدراج. رباعي محدب ا ب ت ثيتم كتابة دائرة إذا وفقط إذا

\tan(\frac(\alpha)(2))\tan(\frac(\gamma)(2))=\tan(\frac(\beta)(2))\tan(\frac(\delta)( 2))=1.

معايير خاصة لتسجيل الشكل الرباعي

الشكل الرباعي البسيط المنقوش (بدون تقاطع ذاتي) هو محدب. يمكن وصف الدائرة حول شكل رباعي محدب إذا وفقط إذا كان مجموع الزوايا المقابلة لها يساوي 180 درجة ( $\باي$ راديان). يمكنك وصف دائرة حول:

أي مضاد متوازي الأضلاع
أي مستطيل (حالة خاصة هي المربع)
أي شبه منحرف متساوي الساقين
أي شكل رباعي له زاويتان قائمتان متقابلتان.

ملكيات

الصيغ ذات الأقطار

ef=ac+bd

;

\frac(e)(f) = \frac(a\cdot d+b\cdot c)(a\cdot b+c\cdot d).

في الصيغة الأخيرة لزوج الجوانب المجاورة للبسط أو د, بو جبقية نهاياتهم على طول قطري ه. بيان مماثل ينطبق على القاسم.

صيغ للأطوال القطرية(عواقب ):

e = \sqrt(\frac((ac+bd)(ad+bc))(ab+cd))

f = \sqrt(\frac((ac+bd)(ab+cd))(ad+bc))

الصيغ مع الزوايا

لشكل رباعي دوري مع سلسلة من الجوانب أ , ب , ج , د، مع نصف محيط صوالزاوية أبين الطرفين أو د، وظائف الزاوية المثلثية أيتم تقديمها بواسطة الصيغ

$\cos A = \frac(a^2 + d^2 - b^2 - c^2)(2(ad + bc))،$ $\sin A = \frac(2\sqrt((p-a)(p-b)(p-c)(p-d)))((ad+bc))),$ $\tan \frac(A)(2) = \sqrt(\frac((p-a)(p-d))((p-b)(p-c))).$

ركن θ وبين الأقطار يوجد:ص26

$\tan \frac(\theta)(2) = \sqrt(\frac((p-b)(p-d))((p-a)(p-c))).$

إذا كان الطرفان متقابلين أو جتتقاطع بزاوية φ ، فهو متساوي

\cos(\frac(\varphi)(2))=\sqrt(\frac((p-b)(p-d)(b+d)^2)((ab+cd)(ad+bc)))،

أين صهناك نصف محيط. :ص 31

نصف قطر الدائرة المحددة حول شكل رباعي

صيغة باراميشفارا

إذا كان شكلاً رباعياً له أضلاع متتالية أ , ب , ج , دوشبه محيط صمنقوشة في دائرة، فإن نصف قطرها يساوي صيغة باراميشوار:ص. 84

$R= \frac(1)(4) \sqrt(\frac((ab+cd)(ad+bc)(ac+bd))((p-a)(p-b)(p-c)(p-d))).$

اشتقها عالم الرياضيات الهندي باراميشوار في القرن الخامس عشر (حوالي 1380–1460).

شكل رباعي محدب (انظر الشكل على اليمين) يتكون من أربع بيانات خطوط ميكيل المستقيمة، يتم إدراجه في دائرة إذا وفقط إذا كانت نقطة ميكيل ميقع الشكل الرباعي على خط يربط بين نقطتين من نقاط تقاطع الخطوط الست (تلك التي ليست رؤوس الشكل الرباعي). ذلك حين ميكمن على إي إف.

ومعيار أن الشكل الرباعي المكون من مثلثين يقع في دائرة معينة

f^2 = \frac((ac+bd)(ad+bc))((ab+cd)).

الشرط الأخير يعطي التعبير عن القطر Fشكل رباعي منقوش في دائرة بأطوال أضلاعه الأربعة ( أ, ب, ج, د). تتبع هذه الصيغة مباشرة عند الضرب وعند مساواة الأجزاء اليسرى واليمنى من الصيغ التي تعبر عن الجوهر نظريات بطليموس الأولى والثانية(أنظر فوق).

معيار أن يتم قطع الشكل الرباعي بخط مستقيم من مثلث في دائرة معينة

إن الخط المستقيم الموازي لجانب المثلث والمتقاطع معه يقطع منه شكلًا رباعيًا يمكن دائمًا وصف الدائرة حوله.
عاقبة. حول مضاد متوازي الأضلاع، حيث يكون الجانبان المتقابلان متضادين متوازيين، من الممكن دائمًا وصف دائرة.

مساحة الشكل الرباعي المدرج في دائرة

الاختلافات في صيغة براهماغوبتا

S=\sqrt((ص-أ)(ص-ب)(ص-ج)(ص-د))،

حيث p هو نصف محيط الشكل الرباعي.

S= \frac(1)(4) \sqrt(- \begin(vmatrix) a & b & c & -d \\ b & a & -d & c \\ c & -d & a & b \\ -d & c & b & a \end(vmatrix))

صيغ المنطقة الأخرى

S = \tfrac(1)(2)(ab+cd)\sin(B)

S = \tfrac(1)(2)(ac+bd)\sin(\theta)،

أين θ أي من الزوايا بين الأقطار. بشرط أن تكون الزاوية أليس خطًا مستقيمًا، ويمكن التعبير عن المساحة أيضًا بـ :ص.26

$S = \tfrac(1)(4)(a^2-b^2-c^2+d^2)\tan(A).$ $\displaystyle S=2R^2\sin(A)\sin(B)\sin(\theta),$

أين رهو نصف قطر الدائرة المحيطة. كنتيجة مباشرة لدينا عدم المساواة

$S\le 2R^2,$

حيث تكون المساواة ممكنة إذا وفقط إذا كان هذا الشكل الرباعي مربعًا.

رباعيات براهماجوبتا

براهماجوبتا رباعي الزواياهو شكل رباعي محفور في دائرة بأطوال أضلاع صحيحة وأقطار صحيحة ومساحة صحيحة. جميع رباعيات براهماجوبتا الممكنة ذات الجوانب أ , ب , ج , د، مع الأقطار ه , F، مع المساحة س، ونصف قطر الدائرة المقيدة ريمكن الحصول عليها عن طريق إزالة مقامات التعبيرات التالية التي تتضمن معلمات عقلانية ر , ش، و الخامس :

$أ=$ $ب=(1+u^2)(v-t)(1+تلفزيون)$ $ج=ر(1+ش^2)(1+ت^2)$ $د=(1+v^2)(ش-ر)(1+تو)$ $ه=ش(1+ت^2)(1+ت^2)$ $و=ت(1+ت^2)(1+ش^2)$ $ق = الأشعة فوق البنفسجية$ $4R=(1+u^2)(1+v^2)(1+t^2).$

أمثلة

الرباعيات المحددة المدرجة في دائرة هي: مستطيل، مربع، متساوي الساقين أو شبه منحرف متساوي الساقين، مضاد متوازي الأضلاع.

رباعيات منقوشة في دائرة ذات أقطار متعامدة (رباعيات متعامدة منقوشة)

خواص الأشكال الرباعية المرسومة في دائرة ذات أقطار متعامدة

محيط ومساحة

بالنسبة للشكل الرباعي المدرج في دائرة ذات أقطار متعامدة، افترض أن تقاطع الأقطار يقسم القطر الواحد إلى أجزاء طولية ص 1 و ص 2، ويقسم القطر الآخر إلى مقاطع طولية س 1 و س 2. ثم (المساواة الأولى هي الاقتراح 11 من أرشميدس" كتاب ليماس)

$د^2=p_1^2+p_2^2+q_1^2+q_2^2=a^2+c^2=b^2+d^2,$

أين د- قطر الدائرة . وهذا صحيح لأن القطرين متعامدان على وتر الدائرة. ويترتب على هذه المعادلات أن نصف قطر الدائرة المقيدة ريمكن كتابتها كما

$R=\tfrac(1)(2)\sqrt(p_1^2+p_2^2+q_1^2+q_2^2)$

أو من حيث أضلاع الشكل الرباعي في الشكل

$R=\tfrac(1)(2)\sqrt(a^2+c^2)=\tfrac(1)(2)\sqrt(b^2+d^2).$

ويترتب على ذلك أيضًا

$أ^2+ب^2+ج^2+د^2=8R^2.$

بالنسبة للأشكال الرباعية القطرية المنقوشة، تنص نظرية براهماجوبتا على ما يلي:

إذا كان الشكل الرباعي الدائري له أقطار متعامدة متقاطعة في نقطة ما $م$ ، ثم زوجين منهمضاد الوسائط تمر عبر نقطة $م$ .

تعليق. في هذه النظرية تحت مكافحة الوسيطفهم الجزء $إف إي.$ شكل رباعي في الشكل الموجود على اليمين (قياسًا على المنصف العمودي (الوسيط) على جانب المثلث). وهو عمودي على أحد الجانبين ويمر في نفس الوقت بمنتصف الجانب الآخر من الشكل الرباعي.

اكتب مراجعة عن مقالة "الأشكال الرباعية المدرج في دائرة"

ملحوظات

برادلي، كريستوفر ج. (2007)، جبر الهندسة: الإحداثيات الديكارتية والمساحية والإسقاطية، الإدراك العالي، ص. 179، ISBN 1906338000، أو سي إل سي
. رباعيات مكتوبة.
سيدونز، إيه دبليو وهيوز، آر تي (1929) علم المثلثات، مطبعة جامعة كامبريدج، ص. 202، O.C.L.C.
دوريل، السيرة الذاتية وروبسون، أ. (2003)، ، ساعي دوفر، ISBN 978-0-486-43229-8 ,
السينا، كلودي ونيلسن، روجر ب. (2007)، ""، المنتدى الهندسيت7: 147-9 ,
جونسون، روجر أ. الهندسة الإقليدية المتقدمة، دوفر للنشر، 2007 (الأصل 1929).
هوهن، لاري (مارس 2000)، “محيط نصف القطر الرباعي الدائري”، الجريدة الرياضيةت 84 (499): 69-70
.
ألتشيلر كورت، ناثان (2007)، هندسة الكلية: مقدمة للهندسة الحديثة للمثلث والدائرة(الطبعة الثانية)، ساعي دوفر، ص. 131، 137–8، ISBN 978-0-486-45805-2، OCLC
هونسبرجر، روس (1995)،،، حلقات في الهندسة الإقليدية في القرنين التاسع عشر والعشرين، المجلد. 37، المكتبة الرياضية الجديدة، مطبعة جامعة كامبريدج، ص. 35-39، ISBN 978-0-88385-639-0
فايستين، اريك دبليو.(باللغة الإنجليزية) على موقع Wolfram MathWorld.
برادلي، كريستوفر (2011)، ,
.
كوكستر، هارولد سكوت ماكدونالد وجريتزر، صامويل إل. (1967)،،، إعادة النظر في الهندسة، الجمعية الرياضية الأمريكية، ص. 57، 60، ISBN 978-0-88385-619-2
.
أندريسكو، تيتو وإنيسكو، بوجدان (2004)، ،، كنوز أولمبياد الرياضيات، سبرينغر، ص. 44-46، 50، ISBN 978-0-8176-4305-8
.
بوخهولز، آر إتش وماكدوغال، جيه إيه (1999)، ""، نشرة جمعية الرياضيات الأستراليةت59 (2): 263–9 ، دوي 10.1017/S0004972700032883
.
جونسون، روجر أ. الهندسة الإقليدية المتقدمة، نشرة دوفر. شركة، 2007
، مع. 74.
.
.
.
بيتر، توماس (سبتمبر 2003)، "تعظيم مساحة الشكل الرباعي"، مجلة كلية الرياضياتت34 (4): 315-6
براسولوف، فيكتور، ,
السينا، كلودي ونيلسن، روجر (2009)،،، ، الرابطة الرياضية الأمريكية، ص. 64، ISBN 978-0-88385-342-9 ,
ساستري، ك.ر.س. (2002). "" (بي دي إف). المنتدى الهندسي 2 : 167–173.
بوسامينتير، ألفريد س. وسالكيند، تشارلز ت. (1970)،،، مشاكل صعبة في الهندسة(الطبعة الثانية)، ساعي دوفر، ص. 104-5، ISBN 978-0-486-69154-1
.
.
.

أنظر أيضا

حسب عدد الجوانب

صحيح

مثلثات

رباعيات

أنظر أيضا

تحتوي المقالة على إشارات قصيرة ("هارفارد") إلى منشورات غير مدرجة أو موصوفة بشكل غير صحيح في القسم الببليوغرافي.
قائمة الروابط المعطلة: , , , , , , , , - حسنًا، ماذا يا القوزاق؟ (تسمى ماريا ديميترييفنا ناتاشا القوزاق) - قالت وهي تداعب يدها ناتاشا التي اقتربت من يدها دون خوف وبمرح. - أعرف أن الجرعة فتاة، لكني أحبها.
لقد أخرجت أقراط ياخون على شكل كمثرى من شبيكتها الضخمة، وأعطتها لنتاشا، التي كانت مبتهجة وحمراء في عيد ميلادها، ابتعدت عنها على الفور والتفتت إلى بيير.
- إيه، إيه! عطوف! "تعال هنا"، قالت بصوت هادئ ورقيق. - هيا يا عزيزتي..
وقد رفعت سواعدها بشكل خطير إلى أعلى.
اقترب بيير ونظر إليها بسذاجة من خلال نظارته.
- تعال، تعال يا عزيزي! لقد كنت الوحيد الذي أخبر والدك بالحقيقة عندما أتيحت له الفرصة، لكن الله أمرك بذلك.
لقد توقفت. كان الجميع صامتين، ينتظرون ما سيحدث، ويشعرون أنه لم يكن هناك سوى مقدمة.
- جيد، لا شيء ليقوله! ولد طيب!... الأب يرقد على سريره، ويسلي نفسه، ويضع الشرطي على دب. إنه عار يا أبي، إنه عار! سيكون من الأفضل الذهاب إلى الحرب.
استدارت ومدت يدها إلى الكونت الذي لم يستطع أن يمنع نفسه من الضحك.
- حسنًا، تعال إلى الطاولة، لدي شاي، هل حان الوقت؟ - قالت ماريا دميترييفنا.
سار الكونت مع ماريا دميترييفنا. ثم الكونتيسة، التي كان يقودها عقيد الحصار، الشخص المناسب الذي كان من المفترض أن يلحق به نيكولاي بالفوج. آنا ميخائيلوفنا - مع شينشين. صافح بيرج مع فيرا. ذهبت جولي كاراجينا مبتسمة مع نيكولاي إلى الطاولة. وخلفهم جاء أزواج آخرون، ممتدين عبر القاعة بأكملها، وخلفهم، واحدًا تلو الآخر، كان هناك أطفال ومعلمون ومربيات. بدأ النوادل في التحرك، واهتزت الكراسي، وبدأت الموسيقى تعزف في الجوقة، وجلس الضيوف في مقاعدهم. تم استبدال أصوات الموسيقى المنزلية للكونت بأصوات السكاكين والشوك وثرثرة الضيوف وخطوات النوادل الهادئة.
في أحد طرفي الطاولة جلست الكونتيسة على رأسها. على اليمين ماريا دميترييفنا، على اليسار آنا ميخائيلوفنا وضيوف آخرون. في الطرف الآخر جلس الكونت، على اليسار العقيد الحصار، على اليمين شينشين وغيرهم من الضيوف الذكور. على أحد جانبي الطاولة الطويلة يوجد شباب أكبر سنًا: فيرا بجوار بيرج، وبيير بجوار بوريس؛ ومن ناحية أخرى - الأطفال والمعلمون والمربيات. من خلف الكريستال والزجاجات ومزهريات الفاكهة، نظر الكونت إلى زوجته وقبعتها الطويلة ذات الأشرطة الزرقاء وسكب النبيذ بجد لجيرانه، دون أن ينسى نفسه. الكونتيسة أيضًا ، من خلف ثمرة الأناناس ، دون أن تنسى واجباتها كربة منزل ، ألقت نظرة كبيرة على زوجها ، الذي بدا لها أن رأسه ووجهه الأصلع كانا مختلفين بشكل حاد عن شعره الرمادي في احمرارهما. كان هناك ثرثرة مستمرة في نهاية السيدات. في غرفة الرجال، سمعت الأصوات أعلى وأعلى، وخاصة العقيد هوسار، الذي أكل وشرب كثيرا، وأحمر الخدود أكثر فأكثر، لدرجة أن الكونت قد جعله بالفعل قدوة للضيوف الآخرين. تحدث بيرج مع فيرا بابتسامة لطيفة أن الحب ليس شعورًا أرضيًا بل شعورًا سماويًا. دعا بوريس صديقه الجديد بيير الضيوف على الطاولة وتبادل النظرات مع ناتاشا التي كانت تجلس مقابله. تحدث بيير قليلاً ونظر إلى الوجوه الجديدة وأكل كثيرًا. بدءًا من نوعين من الحساء، اختار منهما لا تورتو، [السلحفاة،] وكوليبياكي و طيهوج البندق، لم يفوت طبقًا واحدًا ولا نبيذًا واحدًا، والذي وضعه الخادم الشخصي بشكل غامض في زجاجة ملفوفة في منديل من خلف كتف جاره يقول أو "دري ماديرا" أو "المجري" أو "نبيذ الراين". لقد وضع أول كؤوس من الكريستال الأربعة التي تحمل حرف الكونت أمام كل جهاز، وشرب بسرور، ونظر إلى الضيوف بتعبير لطيف بشكل متزايد. نظرت ناتاشا، الجالسة مقابله، إلى بوريس كما تنظر الفتيات البالغات من العمر ثلاثة عشر عامًا إلى الصبي الذي قبلوه للتو لأول مرة والذين يقعون في حبه. هذه النظرة نفسها كانت تتجه أحيانًا إلى بيير، وتحت أنظار هذه الفتاة المضحكة والمفعمة بالحيوية أراد أن يضحك، دون أن يعرف السبب.
جلس نيكولاي بعيدًا عن سونيا، بجوار جولي كاراجينا، وتحدث معها مرة أخرى بنفس الابتسامة اللاإرادية. ابتسمت سونيا بشكل رائع، ولكن على ما يبدو كانت تعذبها الغيرة: لقد تحولت إلى شاحب، ثم احمر خجلا واستمعت بكل قوتها إلى ما يقوله نيكولاي وجولي لبعضهما البعض. نظرت المربية حولها بقلق، وكأنها تستعد للرد إذا قرر أي شخص الإساءة إلى الأطفال. حاول المعلم الألماني حفظ جميع أنواع الأطباق والحلويات والنبيذ من أجل وصف كل شيء بالتفصيل في رسالة إلى عائلته في ألمانيا، وقد شعر بالإهانة الشديدة من حقيقة أن كبير الخدم كان يحمل زجاجة ملفوفة في منديل. حوله. عبوس الألماني، حاول إظهار أنه لا يريد الحصول على هذا النبيذ، لكنه شعر بالإهانة لأنه لا أحد يريد أن يفهم أنه يحتاج إلى النبيذ حتى لا يروي عطشه، ليس بسبب الجشع، ولكن بدافع الفضول الضميري.

في نهاية الطاولة، أصبحت المحادثة أكثر حيوية. قال العقيد إن بيان إعلان الحرب قد نُشر بالفعل في سانت بطرسبرغ وأن النسخة التي رآها بنفسه قد تم تسليمها الآن عن طريق البريد إلى القائد الأعلى.
- ولماذا يصعب علينا محاربة بونابرت؟ - قال شينشين. – II a deja rabattu le caquet a l "Autriche. Je crins، que cette fois ce ne soit notre Tour. [لقد حطم بالفعل غطرسة النمسا. وأخشى أن دورنا لن يأتي الآن.]
كان العقيد ألمانيًا ممتلئ الجسم، طويل القامة، ومتفائلًا، وكان من الواضح أنه خادم ووطني. لقد شعر بالإهانة من كلمات شينشين.
"وبعد ذلك، نحن دولة ذات سيادة جيدة"، قال، وهو ينطق e بدلاً من e و ъ بدلاً من ь. "ثم أن الإمبراطور يعرف ذلك، وقال في بيانه إنه يستطيع أن ينظر بلا مبالاة إلى المخاطر التي تهدد روسيا، وأن سلامة الإمبراطورية وكرامتها وقدسية تحالفاتها"، لسبب ما، مؤكدا بشكل خاص. كلمة "نقابات" وكأن هذا هو جوهر الأمر برمته.
وبذاكرته الرسمية المعصومة من الخطأ، كرر الكلمات الافتتاحية للبيان... "والرغبة، الهدف الوحيد الذي لا غنى عنه للملك: إحلال السلام في أوروبا على أسس متينة - قرروا الآن إرسال جزء من الجيش في الخارج وبذل جهود جديدة لتحقيق هذه النية”.
واختتم كلمته قائلاً: "لهذا السبب، نحن ملك جيد"، وهو يشرب كأساً من النبيذ وينظر إلى الكونت من أجل التشجيع.
– تعرف على المثل: [أنت تعرف المثل القائل:] “إيريما، إيريما، يجب أن تجلسي في المنزل، تشحذين مغازلك،” قال شينشين وهو يتلوى ويبتسم. – نحن نتوافق مع الرائع. [هذا مفيد بالنسبة لنا.] لماذا سوفوروف - لقد قطعوه، طبقًا من تصميم الأزياء، [على رأسه،] وأين سوفوروف لدينا الآن؟ Je vous requiree un peu, [أنا أسألك] - قال وهو يقفز باستمرار من الروسية إلى الفرنسية.
قال العقيد وهو يضرب الطاولة: "علينا أن نقاتل حتى آخر قطرة دم، ونموت من أجل إمبراطورنا، وبعد ذلك سيكون كل شيء على ما يرام". "وللجادل قدر الإمكان (وخاصة أنه شدد صوته على كلمة "ممكن")، بأقل قدر ممكن،" انتهى، والتفت مرة أخرى إلى العد. "هذه هي الطريقة التي نحكم بها على الفرسان القدامى، هذا كل شيء." كيف تحكم أيها الشاب والحصار الشاب؟ - أضاف متوجهاً إلى نيكولاي الذي سمع أن الأمر يتعلق بالحرب وترك محاوره ونظر بكل عينيه واستمع إلى العقيد بكل أذنيه.
"أنا أتفق معك تمامًا"، أجاب نيكولاي، وقد احمر وجهه، وهو يدير الطبق ويعيد ترتيب الكؤوس بنظرة حاسمة ويائسة، كما لو كان معرضًا لخطر كبير في تلك اللحظة، "أنا مقتنع بأن الروس يجب أن يموتوا". "أو الفوز"، قال، وهو يشعر بنفس الشعور الذي يشعر به الآخرون، بعد أن قيلت الكلمة بالفعل، حيث كان الأمر متحمسًا ومبهجًا للغاية بالنسبة للمناسبة الحالية، وبالتالي فهو محرج.
""C"est bien beau ce que vous venez de dire، [رائع! ما قلته رائع]،" قالت جولي، التي كانت تجلس بجانبه، وهي تتنهد. ارتجفت سونيا في كل مكان واحمر خجلاً حتى الأذنين، خلف الأذنين و إلى الرقبة والكتفين، بينما كان نيكولاي يتحدث، استمع بيير إلى خطب العقيد وأومأ برأسه بالموافقة.
قال: "هذا جميل".
صاح العقيد وهو يضرب الطاولة مرة أخرى: "هوسار حقيقي أيها الشاب".
-ما الذي تثيرين الضجيج هناك؟ - سمع فجأة صوت ماريا دميترييفنا الجهير عبر الطاولة. -لماذا تطرق على الطاولة؟ - التفتت إلى الحصار - من أنت متحمس؟ صحيح، هل تعتقد أن الفرنسيين أمامك؟
قال الحصار مبتسماً: "أنا أقول الحقيقة".
صاح الكونت عبر الطاولة: "كل شيء يتعلق بالحرب". - بعد كل شيء، ابني قادم، ماريا دميترييفنا، ابني قادم.
- ولدي أربعة أبناء في الجيش، لكني لا أنزعج. "كل شيء هو مشيئة الله: سوف تموت مستلقيًا على الموقد، وفي المعركة سوف يرحمك الله،" بدا صوت ماريا دميترييفنا الغليظ دون أي جهد من الطرف الآخر من الطاولة.
- هذا صحيح.
وتركزت المحادثة مرة أخرى - السيدات في نهاية الطاولة، والرجال في جانبه.
قال الأخ الصغير لنتاشا: «لكنك لن تسأل، لكنك لن تسأل!»
أجابت ناتاشا: "سأسأل".
احمر وجهها فجأة، معبرة عن تصميمها اليائس والمبهج. وقفت ودعت بيير الذي كان يجلس مقابلها للاستماع والتفتت إلى والدتها:
- الأم! - بدا صوتها الطفولي الصدور عبر الطاولة.
- ماذا تريد؟ - سألت الكونتيسة بخوف، ولكن عندما رأت من وجه ابنتها أنها مزحة، لوحت بيدها بشدة، وأبدت لفتة تهديدية وسلبية برأسها.
المحادثة هدأت.
- الأم! أي نوع من الكعكة سيكون؟ - بدا صوت ناتاشا أكثر حزما، دون أن ينهار.
أرادت الكونتيسة العبوس، لكنها لم تستطع. هزت ماريا دميترييفنا إصبعها الغليظ.
قالت بتهديد: "القوزاق".
نظر معظم الضيوف إلى الشيوخ، ولا يعرفون كيفية اتخاذ هذه الحيلة.
- هنا أنا! - قالت الكونتيسة.
- الأم! أي نوع من الكعكة سيكون هناك؟ - صرخت ناتاشا الآن بمرح بجرأة ومتقلبة، واثقة مسبقًا من أن مقلبها سيكون موضع ترحيب.
كانت سونيا وبيتيا السمينة مختبئتين من الضحك.
"لهذا السبب سألت"، همست ناتاشا لأخيها الصغير وبيير، الذي نظرت إليه مرة أخرى.
قالت ماريا دميترييفنا: "الآيس كريم، لكنهم لن يعطوه لك".
رأت ناتاشا أنه لا يوجد شيء يخاف منه، وبالتالي لم يكن خائفا من ماريا دميترييفنا.
- ماريا دميترييفنا؟ ما الآيس كريم! أنا لا أحب كريم.
- جزرة.
- لا، أي واحد؟ ماريا دميترييفنا، أي واحد؟ - صرخت تقريبا. - أريد أن أعرف!
ضحكت ماريا دميترييفنا والكونتيسة، وتبعهما جميع الضيوف. لم يضحك الجميع على إجابة ماريا دميترييفنا، بل على الشجاعة غير المفهومة وبراعة هذه الفتاة، التي عرفت كيف وتجرأت على معاملة ماريا دميترييفنا بهذه الطريقة.
تأخرت ناتاشا فقط عندما قيل لها أنه سيكون هناك أناناس. تم تقديم الشمبانيا قبل الآيس كريم. بدأت الموسيقى تعزف مرة أخرى، وقبل الكونت الكونتيسة، ووقف الضيوف وهنأوا الكونتيسة، وقرعوا الكؤوس على الطاولة مع الكونت والأطفال وبعضهم البعض. ركض النوادل مرة أخرى، واهتزت الكراسي، وبنفس الترتيب، ولكن بوجوه أكثر احمرارًا، عاد الضيوف إلى غرفة المعيشة ومكتب الكونت.

تم فصل طاولات بوسطن عن بعضها البعض، وتم ترتيب الحفلات، واستقر ضيوف الكونت في غرفتي معيشة وغرفة أريكة ومكتبة.
الكونت، الذي نشر أوراقه، لم يستطع مقاومة عادة أخذ قيلولة بعد الظهر والضحك على كل شيء. تجمع الشباب، بتحريض من الكونتيسة، حول الكلافيكورد والقيثارة. كانت جولي أول من عزف مقطوعة على القيثارة، بناءً على طلب الجميع، وبدأت مع فتيات أخريات في مطالبة ناتاشا ونيكولاي، المعروفين بموسيقاهما، بغناء شيء ما. يبدو أن ناتاشا، التي تم التعامل معها على أنها فتاة كبيرة، كانت فخورة جدًا بهذا، لكنها كانت خجولة في نفس الوقت.
- ماذا سنغني؟ - هي سألت.
أجاب نيكولاي: "المفتاح".
- حسنا، دعونا نسرع. قالت ناتاشا: "بوريس، تعال إلى هنا". - أين سونيا؟
نظرت حولها، ورأت أن صديقتها لم تكن في الغرفة، فركضت خلفها.
ركضت ناتاشا إلى غرفة سونيا ولم تجد صديقتها هناك، وركضت إلى الحضانة - ولم تكن سونيا هناك. أدركت ناتاشا أن سونيا كانت في الممر على صدرها. كان الصندوق الموجود في الممر مكانًا للحزن على جيل الإناث الأصغر سناً في منزل روستوف. في الواقع، سونيا في فستانها الوردي متجدد الهواء، سحقته، استلقت على سرير الريش المخطط القذر الخاص بمربيتها، على صدرها، وغطت وجهها بأصابعها، وبكت بمرارة، وهزت أكتافها العارية. وجه ناتاشا المتحرك، مع عيد ميلاد طوال اليوم، تغير فجأة: توقفت عيناها، ثم ارتجفت رقبتها العريضة، وتدلت زوايا شفتيها.
- سونيا! ما أنت؟... ماذا، ما بك؟ واو واو!…
وبدأت ناتاشا، التي فتحت فمها الكبير وأصبحت غبية تمامًا، في الزئير كطفل، دون أن تعرف السبب وفقط لأن سونيا كانت تبكي. أرادت سونيا رفع رأسها، أرادت الإجابة، لكنها لم تستطع واختبأت أكثر. بكت ناتاشا وهي تجلس على سرير من الريش الأزرق وتعانق صديقتها. بعد أن استجمعت قوتها، وقفت سونيا وبدأت تمسح دموعها وتحكي القصة.
- نيكولينكا ستغادر بعد أسبوع،... ورقته... خرجت... قال لي بنفسه... نعم، ما زلت لا أبكي... (أظهرت قطعة الورق التي كانت تحملها) يدها: كان شعرًا من تأليف نيكولاي) مازلت لا أبكي، لكنك لم تفعل ذلك، لا أحد يستطيع أن يفهم... أي نوع من الروح لديه.
وبدأت في البكاء مرة أخرى لأن روحه كانت طيبة جدًا.
قالت وقد استجمعت بعض القوة: "أنت تشعر بالارتياح... أنا لا أحسدك... أنا أحبك، وأحب بوريس أيضًا، إنه لطيف... لا توجد عوائق أمامك". ونيكولاي هو ابن عمي... أحتاج... المتروبوليت نفسه... وهذا مستحيل. وبعد ذلك، إذا ماما... (سونيا نظرت إلى الكونتيسة واتصلت بوالدتها)، ستقول إنني أدمر مهنة نيكولاي، وليس لدي قلب، وأنني جاحدة للجميل، ولكن حقًا... في سبيل الله... (رسمت علامة الصليب) وأنا أحبها كثيراً أيضاً، وأنتم جميعاً، فقط فيرا... لماذا؟ ماذا فعلت لها؟ أنا ممتنة لك لدرجة أنني سأكون سعيدًا بالتضحية بكل شيء، لكن ليس لدي أي شيء.
لم تعد سونيا قادرة على الكلام وأخفت رأسها مرة أخرى بين يديها وسرير الريش. بدأت ناتاشا تهدأ، لكن كان واضحاً من وجهها أنها تفهم أهمية حزن صديقتها.
- سونيا! - قالت فجأة وكأنها خمنت السبب الحقيقي لحزن ابن عمها. - هذا صحيح، تحدثت معك فيرا بعد العشاء؟ نعم؟
– نعم، نيكولاي نفسه كتب هذه القصائد، وأنا نسخت غيرها؛ لقد وجدتهم على طاولتي وقالت إنها ستعرضهم على ماما، وقالت أيضًا إنني كنت جاحدًا، وأن ماما لن تسمح له أبدًا بالزواج مني، وسيتزوج جولي. ترى كيف هو معها طوال اليوم... ناتاشا! لماذا؟…
ومرة أخرى بكت بمرارة أكثر من ذي قبل. رفعتها ناتاشا وعانقتها وبدأت تبتسم من خلال دموعها في تهدئتها.
- سونيا، لا تصدقيها، عزيزتي، لا تصدقيها. هل تتذكر كيف تحدثنا نحن الثلاثة مع نيكولينكا في غرفة الأريكة؛ تذكر بعد العشاء؟ بعد كل شيء، قررنا كل شيء كيف سيكون. لا أتذكر كيف، لكنك تتذكر كيف كان كل شيء جيدًا وكان كل شيء ممكنًا. شقيق العم شينشين متزوج من ابن عمه، ونحن أبناء عمومة من الدرجة الثانية. وقال بوريس أن هذا ممكن جدًا. كما تعلمون، لقد أخبرته بكل شيء. قالت ناتاشا: "إنه ذكي جدًا وجيد جدًا" ... "أنت يا سونيا، لا تبكي، يا عزيزتي، يا عزيزتي، سونيا". - وقبلتها وهي تضحك. - فيرا شريرة بارك الله فيها! لكن كل شيء سيكون على ما يرام، ولن تخبر ماما؛ سيقول نيكولينكا ذلك بنفسه، ولم يفكر حتى في جولي.
وقبلتها على رأسها. وقفت سونيا، وانتعشت القطة، وتألقت عيناها، وبدا أنه مستعد للتلويح بذيله، والقفز على كفوفه الناعمة واللعب بالكرة مرة أخرى، كما كان مناسبًا له.
- كنت أعتقد؟ يمين؟ بواسطة الله؟ - قالت وهي تعدل فستانها وشعرها بسرعة.
- حقا والله! - أجابت ناتاشا وهي تقوم بتسوية خصلة من الشعر الخشن تحت جديلة صديقتها.
وكلاهما ضحكا.
- حسنًا، لنغني "المفتاح".
- لنذهب إلى.
"كما تعلمون، هذا بيير السمين الذي كان يجلس أمامي مضحك للغاية!" - قالت ناتاشا فجأة وتوقفت. - أنا أستمتع كثيرًا!
وركضت ناتاشا عبر الممر.
سونيا، تنفض الزغب وتخفي القصائد في حضنها، حتى رقبتها بعظام الصدر البارزة، بخطوات خفيفة ومبهجة، مع وجه محمر، ركضت خلف ناتاشا على طول الممر إلى الأريكة. بناء على طلب الضيوف، غنى الشباب الرباعية "المفتاح"، والتي أحبها الجميع حقا؛ ثم غنى نيكولاي الأغنية التي تعلمها مرة أخرى.
في ليلة سعيدة، في ضوء القمر،
تخيل نفسك سعيدا
أنه لا يزال هناك شخص ما في العالم،
ومن يفكر فيك أيضاً!
كما قالت بيدها الجميلة
المشي على طول القيثارة الذهبية ،
مع انسجامها العاطفي
يدعو إلى نفسه، يدعوك!
يوم آخر أو يومين وستأتي الجنة...
لكن اه! صديقك لن يعيش!
ولم يكن قد انتهى بعد من غناء الكلمات الأخيرة عندما كان الشباب في القاعة يستعدون للرقص وبدأ الموسيقيون في الجوقة يطرقون أقدامهم ويسعلون.

كان بيير جالسا في غرفة المعيشة، حيث بدأ شينشين، كما لو كان مع زائر من الخارج، معه محادثة سياسية مملة لبيير، والتي انضم إليها الآخرون. عندما بدأت الموسيقى، دخلت ناتاشا غرفة المعيشة، وذهبت مباشرة إلى بيير، وهي تضحك وتحمر خجلاً، وقالت:
- أمي قالت لي أن أطلب منك الرقص.
قال بيير: "أخشى أن أخلط بين الأرقام، ولكن إذا كنت تريد أن تكون أستاذي..."
ومد يده الغليظة، وخفضها إلى مستوى منخفض، للفتاة النحيلة.
بينما كان الأزواج يستقرون والموسيقيون يستعدون، جلس بيير مع سيدته الصغيرة. كانت ناتاشا سعيدة تماما؛ رقصت مع شخص كبير، مع شخص جاء من الخارج. جلست أمام الجميع وتحدثت معه كفتاة كبيرة. كان لديها مروحة في يدها، أعطتها لها سيدة شابة لتمسك بها. وبافتراض الوضع الأكثر علمانية (الله أعلم أين ومتى تعلمت ذلك)، تحدثت إلى رجلها، وهي تهوي وتبتسم من خلال المروحة.
- ما هو، ما هو؟ "انظري، انظري"، قالت الكونتيسة العجوز وهي تمر عبر القاعة وتشير إلى ناتاشا.
احمر خجلا ناتاشا وضحكت.
-حسنا ماذا عنك يا أمي؟ حسنًا، ما نوع الصيد الذي تبحث عنه؟ ما الذي يثير الدهشة هنا؟

في منتصف الجلسة البيئية الثالثة، بدأت الكراسي في غرفة المعيشة، حيث كان الكونت وماريا دميترييفنا يلعبان، تتحرك، وتمدد معظم الضيوف الكرام وكبار السن بعد جلوس طويل ووضعوا المحافظ والمحافظ في جيوبهم وخرجوا من أبواب القاعة. تقدمت ماريا دميترييفنا بالعد - وكلاهما بوجوه مرحة. مد الكونت، بأدب مرح، مثل الباليه، يده المستديرة إلى ماريا دميترييفنا. استقام، وأضاء وجهه بابتسامة شجاعة وماكرة بشكل خاص، وبمجرد رقص آخر شخصية من الإيكوزا، صفق بيديه للموسيقيين وصرخ للجوقة مخاطبًا الكمان الأول:
- سيميون! هل تعرف دانيلا كوبور؟
كانت هذه رقصة الكونت المفضلة التي رقصها في شبابه. (كان دانيلو كوبور في الواقع أحد شخصيات الملائكة.)
"انظر إلى أبي" ، صرخت ناتاشا في القاعة بأكملها (نسيت تمامًا أنها كانت ترقص مع واحدة كبيرة) ، وحنت رأسها المجعد إلى ركبتيها وانفجرت في ضحكها الرنان في جميع أنحاء القاعة.
في الواقع، نظر كل من في القاعة بابتسامة فرح إلى الرجل العجوز المبتهج، الذي كان بجانب سيدته الكريمة ماريا دميترييفنا، التي كانت أطول منه، يلتف ذراعيه، ويهزهما في الوقت المناسب، ويقوّم كتفيه، ويلوي ذراعيه. ساقيه، وختم قدميه قليلاً، وبابتسامة تتفتح بشكل متزايد على وجهه المستدير، قام بإعداد الجمهور لما سيأتي. بمجرد سماع أصوات دانيلا كوبور المبهجة والمتحدية، مثل الثرثرة المبهجة، امتلأت جميع أبواب القاعة فجأة بوجوه الرجال من جهة ووجوه النساء المبتسمة للخدم من الجانب الآخر، الذين خرجوا إلى انظر إلى السيد المرح.
- الأب لنا! نسر! - قالت المربية بصوت عال من باب واحد.
رقص الكونت جيدًا وكان يعرف ذلك، لكن سيدته لم تكن تعرف كيف ولم ترغب في الرقص جيدًا. كان جسدها الضخم منتصبًا وذراعيها القويتين متدليتين (أعطت الشبكة للكونتيسة) ؛ فقط وجهها الصارم ولكن الجميل كان يرقص. ما تم التعبير عنه في الشكل المستدير بأكمله للكونت، في ماريا دميترييفنا، تم التعبير عنه فقط في وجه مبتسم بشكل متزايد وأنف مرتعش. ولكن إذا كان الكونت، الذي أصبح غير راضٍ أكثر فأكثر، أسر الجمهور بمفاجأة الالتواءات الماهرة والقفزات الخفيفة لساقيه الناعمتين، فإن ماريا دميترييفنا، مع أدنى حماسة في تحريك كتفيها أو تقريب ذراعيها بالتناوب والضغط، لم تفعل شيئًا. أقل انطباعًا عن الجدارة، وهو الأمر الذي يقدره الجميع بسبب بدانتها وشدتها الدائمة. أصبحت الرقصة متحركة أكثر فأكثر. لم يتمكن النظراء من جذب الانتباه إلى أنفسهم لمدة دقيقة ولم يحاولوا حتى القيام بذلك. كل شيء كان مشغولاً بالكونت وماريا دميترييفنا. قامت ناتاشا بسحب أكمام وفساتين جميع الحاضرين، الذين كانوا يراقبون أعينهم بالفعل على الراقصين، وطالبتهم بالنظر إلى أبي. خلال فترات الرقص، أخذ الكونت نفسًا عميقًا، ولوح للموسيقيين وصرخ بهم ليعزفوا بسرعة. أسرع وأسرع وأسرع وأسرع وأسرع، انكشف العد، ثم على أطراف أصابعه، ثم على الكعب، وهو يندفع حول ماريا دميترييفنا، وأخيرًا، حول سيدته إلى مكانها، وقام بالخطوة الأخيرة، ورفع ساقه الناعمة من أعلى خلفه، يحني رأسه المتعرق بوجه مبتسم ويلوح بيده اليمنى بشكل مستدير وسط هدير التصفيق والضحك، خاصة من ناتاشا. توقف كلا الراقصين، وهما يلهثان بشدة ويمسحان نفسيهما بمناديل كامبريك.
قال الكونت: "هكذا رقصوا في عصرنا يا سيدي".
- أوه نعم دانيلا كوبور! - قالت ماريا دميترييفنا وهي تطلق الروح بقوة ولفترة طويلة وهي تشمر عن سواعدها.

بينما كان آل روستوف يرقصون الأغنية الإنجليزية السادسة في القاعة على أصوات الموسيقيين المتعبين غير المتناغمين، وكان النوادل والطهاة المتعبون يعدون العشاء، ضربت الضربة السادسة الكونت بيزوخي. أعلن الأطباء أنه لا يوجد أمل في الشفاء؛ تم إعطاء المريض اعترافًا صامتًا وتواصلًا؛ كانوا يستعدون للمسحة، وفي المنزل كان هناك صخب وقلق من الترقب، وهو أمر شائع في مثل هذه اللحظات. خارج المنزل، خلف البوابة، احتشد متعهدو دفن الموتى، مختبئين من العربات المقتربة، في انتظار أمر ثري لجنازة الكونت. القائد الأعلى لموسكو، الذي أرسل باستمرار مساعدين للاستفسار عن منصب الكونت، جاء في ذلك المساء ليودع نبيل كاثرين الشهير، الكونت بيزوخيم.
كانت غرفة الاستقبال الرائعة ممتلئة. وقف الجميع باحترام عندما خرج القائد الأعلى من هناك، بعد أن كان بمفرده مع المريض لمدة نصف ساعة تقريبًا، وأعاد الأقواس قليلاً وحاول في أسرع وقت ممكن تجاوز أنظار الأطباء ورجال الدين والأقارب ثابت عليه. الأمير فاسيلي، الذي فقد وزنه وشحب خلال هذه الأيام، ودع القائد الأعلى وكرر له بهدوء شيئًا ما عدة مرات.
بعد وداع القائد الأعلى، جلس الأمير فاسيلي بمفرده على كرسي في القاعة، وعقد ساقيه عالياً، وأسند مرفقه على ركبته وأغمض عينيه بيده. بعد أن جلس هكذا لبعض الوقت، وقف وبخطوات متسرعة بشكل غير عادي، ونظر حوله بعيون خائفة، ومشى عبر الممر الطويل إلى النصف الخلفي من المنزل، إلى الأميرة الكبرى.
كان الموجودون في الغرفة ذات الإضاءة الخافتة يتحدثون همسًا غير متكافئ مع بعضهم البعض ويصمتون في كل مرة، ونظروا بعيون مليئة بالتساؤل والتوقع إلى الباب المؤدي إلى غرف الرجل المحتضر وأصدروا صوتًا خافتًا عندما خرج شخص ما. منه أو دخلت عليه.
قال الرجل العجوز، وهو رجل دين، للسيدة التي جلست بجانبه واستمعت إليه بسذاجة: "الحدود البشرية، لقد تم وضع الحد، لا يمكنك تجاوزه".
"أتساءل عما إذا كان الوقت قد فات لإجراء المسحة؟" - سألت السيدة بإضافة اللقب الروحي، وكأن ليس لديها رأي خاص بها في هذا الشأن.

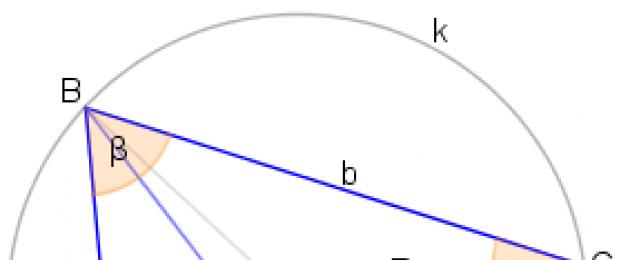
"دائرة"لقد رأينا أنه يمكن تحديد دائرة حول أي مثلث. أي أن لكل مثلث دائرة بحيث "تجلس" عليها رؤوس المثلث الثلاثة. مثله:

سؤال: هل يمكن قول الشيء نفسه عن الشكل الرباعي؟ هل صحيح أنه ستكون هناك دائمًا دائرة "تجلس" عليها جميع القمم الأربعة للشكل الرباعي؟

اتضح أن هذا ليس صحيحا! لا يمكن دائمًا إدراج الشكل الرباعي في دائرة. هناك شرط مهم جداً:

في صورتنا:

انظر، الزوايا تقع مقابل بعضها البعض، مما يعني أنهما متقابلان. ماذا بعد ذلك عن الزوايا و؟ يبدو أنهما متضادان أيضًا؟ هل من الممكن أن تأخذ الزوايا وبدلا من الزوايا و؟

بالتأكيد تستطيع! الشيء الرئيسي هو أن الشكل الرباعي له زاويتان متقابلتان، سيكون مجموعهما. ثم سيتم إضافة الزاويتين المتبقيتين من تلقاء نفسها أيضًا. لا تصدق؟ دعونا نتأكد. ينظر:

اسمحوا ان. هل تتذكر ما هو مجموع الزوايا الأربع لأي شكل رباعي؟ بالتأكيد، . وهذا هو - دائما! . لكن → .

السحر هناك!

لذا تذكر هذا بقوة:

إذا كان الشكل الرباعي محصورا في دائرة، فإن مجموع أي زاويتين متقابلتين له يساوي

والعكس صحيح:

إذا كان الشكل الرباعي له زاويتان متقابلتان مجموعهما متساو، فإن الشكل الرباعي يكون دائريًا.

لن نثبت كل هذا هنا (إذا كنت مهتمًا، فابحث في المستويات النظرية التالية). لكن دعونا نرى ما تؤدي إليه هذه الحقيقة الرائعة: أنه في الشكل الرباعي المنقوش يكون مجموع الزوايا المتقابلة متساويًا.

على سبيل المثال، يتبادر إلى الذهن السؤال: هل من الممكن وصف دائرة حول متوازي الأضلاع؟ دعونا نجرب "طريقة الوخز" أولاً.

بطريقة ما لا ينجح الأمر.

الآن دعونا نطبق المعرفة:

لنفترض أننا تمكنا بطريقة ما من وضع دائرة في متوازي الأضلاع. ثم يجب أن يكون هناك بالتأكيد: أي.

الآن دعونا نتذكر خصائص متوازي الأضلاع:

كل متوازي أضلاع له زوايا متقابلة متساوية.

اتضح ذلك

ماذا عن الزوايا و؟ حسنا، نفس الشيء بالطبع.

منقوش → →

متوازي الأضلاع → →

مذهل، أليس كذلك؟

اتضح أنه إذا تم إدراج متوازي الأضلاع في دائرة، فإن جميع زواياه متساوية، أي أنه مستطيل!

وفي نفس الوقت - يتطابق مركز الدائرة مع نقطة تقاطع أقطار هذا المستطيل. يتم تضمين هذا كمكافأة، إذا جاز التعبير.

حسنًا، هذا يعني أننا اكتشفنا أن متوازي الأضلاع محصور في دائرة مستطيل.

الآن دعونا نتحدث عن شبه منحرف. ماذا يحدث إذا تم رسم شبه منحرف في دائرة؟ولكن اتضح أنه سيكون هناك شبه منحرف متساوي الساقين. لماذا؟

دع شبه المنحرف يتم إدراجه في دائرة. ثم مرة أخرى، ولكن بسبب توازي الخطوط و.

هذا يعني أن لدينا: → → شبه منحرف متساوي الساقين.

حتى أسهل من المستطيل، أليس كذلك؟ لكن عليك أن تتذكر بحزم - سيكون ذلك مفيدًا:

دعونا ندرج أهمها مرة أخرى البيانات الرئيسيةمماس للشكل الرباعي المدرج في دائرة:

يكون الشكل الرباعي محصوراً في دائرة إذا وفقط إذا كان مجموع الزاويتين المتقابلتين له يساوي
متوازي الأضلاع منقوش في دائرة - بالتأكيد مستطيلويتطابق مركز الدائرة مع نقطة تقاطع الأقطار
شبه المنحرف المدرج في دائرة متساوي الأضلاع.

رباعي منقوش. مستوى متوسط

ومعلوم أن لكل مثلث دائرة مقيدة (وقد أثبتنا ذلك في موضوع "الدائرة المحصورة"). ماذا يمكن أن يقال عن الرباعي؟ لقد أتضح أن لا يمكن إدراج كل شكل رباعي في دائرة، وهناك مثل هذه النظرية:

يكون الشكل الرباعي محصوراً في دائرة إذا وفقط إذا كان مجموع زواياه المقابلة يساوي.

في رسمنا -

دعونا نحاول أن نفهم لماذا هذا؟ بمعنى آخر، سنثبت الآن هذه النظرية. ولكن قبل أن تثبت ذلك، عليك أن تفهم كيف تعمل العبارة نفسها. هل لاحظت عبارة "ثم وبعد ذلك فقط" في البيان؟ مثل هذه الكلمات تعني أن علماء الرياضيات الضارين قد حشروا عبارتين في عبارة واحدة.

دعونا فك التشفير:

"ثم" تعني: إذا كان الشكل الرباعي محصورا في دائرة، فإن مجموع أي زاويتين متقابلتين فيه يكون متساويا.
"عندها فقط" تعني: إذا كان للشكل الرباعي زاويتان متقابلتان مجموعهما متساو، فيمكن إدراج هذا الرباعي في دائرة.

تمامًا مثل أليس: "أنا أفكر فيما أقول" و"أقول ما أعتقده".

الآن دعونا نكتشف لماذا كلا من 1 و 2 صحيحان؟

الأول 1.

دع الشكل الرباعي يتم إدراجه في دائرة. دعونا نحدد مركزها ونرسم أنصاف الأقطار و. ماذا سيحدث؟ هل تتذكر أن الزاوية المحيطية تساوي نصف قياس الزاوية المركزية المقابلة لها؟ إذا تذكرت سنطبقه الآن، وإذا لم تتذكره فراجع الموضوع "دائرة. الزاوية المرسومة".

منقوشة

لكن انظر: .

لقد حصلنا على ذلك إذا - منقوش، إذن

حسنًا، من الواضح أنه يضيف شيئًا أيضًا. (تحتاج أيضًا إلى التفكير).

والآن "بالعكس" أي 2.

لنتبين أنه في الشكل الرباعي يكون مجموع زاويتين متقابلتين متساويًا. دعنا نقول دعونا

لا نعرف حتى الآن ما إذا كان بإمكاننا وصف دائرة حولها. لكننا نعلم يقينًا أنه يمكننا بالتأكيد وصف دائرة حول مثلث. لنفعلها اذا.

إذا لم "تجلس" النقطة على الدائرة، فسينتهي بها الأمر حتماً إما بالخارج أو بالداخل.

دعونا ننظر في كلتا الحالتين.

دع النقطة تكون بالخارج أولاً. ثم يتقاطع الجزء مع الدائرة عند نقطة ما. دعونا نتواصل و. والنتيجة هي شكل رباعي منقوش (!).

ونحن نعلم بالفعل أن مجموع الزوايا المتقابلة لها متساوٍ، أي وفقًا لحالتنا.

اتضح أنه ينبغي أن يكون الأمر كذلك.

لكن هذا لا يمكن أن يكون هو الحال لأن - هي زاوية خارجية لـ ووسيلة.

ماذا عن الداخل؟ دعونا نفعل أشياء مماثلة. دع النقطة تكون في الداخل.

ثم يتقاطع استمرار القطعة مع الدائرة عند نقطة ما. مرة أخرى - شكل رباعي منقوش، ووفقًا للشرط يجب أن يكون راضيًا، ولكن - زاوية خارجية للوسائل، أي مرة أخرى لا يمكن أن تكون كذلك.

أي أن النقطة لا يمكن أن تكون خارج الدائرة أو داخلها - وهذا يعني أنها تقع على الدائرة!

لقد تم إثبات النظرية بأكملها!

الآن دعونا نرى ما هي العواقب الجيدة التي تعطيها هذه النظرية.

النتيجة الطبيعية 1

متوازي الأضلاع المدرج في دائرة لا يمكن أن يكون إلا مستطيلاً.

دعونا نفهم لماذا هذا هو الحال. دع متوازي الأضلاع يُدرج في دائرة. ثم ينبغي القيام به.

لكن من خصائص متوازي الأضلاع نعرف ذلك.

ونفس الشيء، بطبيعة الحال، فيما يتعلق بالزوايا و.

لذلك اتضح أنه مستطيل - كل الزوايا على طول.

ولكن، بالإضافة إلى ذلك، هناك حقيقة ممتعة إضافية: يتطابق مركز الدائرة المحيطة بالمستطيل مع نقطة تقاطع الأقطار.

دعونا نفهم لماذا. أتمنى أن تتذكر جيدًا أن الزاوية المقابلة للقطر هي خط مستقيم.

قطر الدائرة،

قطر الدائرة

مما يعني أنه المركز. هذا كل شئ.

النتيجة الطبيعية 2

شبه المنحرف المدرج في دائرة هو متساوي الساقين.

دع شبه المنحرف يتم إدراجه في دائرة. ثم.

و أيضا.

هل ناقشنا كل شيء؟ ليس حقيقيًا. في الواقع، هناك طريقة "سرية" أخرى للتعرف على الشكل الرباعي المنقوش. لن نقوم بصياغة هذه الطريقة بشكل صارم للغاية (ولكن بشكل واضح)، لكننا سنثبتها فقط في المستوى الأخير من النظرية.

إذا كان من الممكن ملاحظة مثل هذه الصورة في الشكل الرباعي كما هو الحال هنا في الشكل (هنا الزوايا "تنظر" إلى جانب النقاط وتكون متساوية)، فسيتم إدراج هذا الشكل الرباعي.

هذا رسم مهم جدًا - في المسائل غالبًا ما يكون من الأسهل العثور على زوايا متساوية بدلاً من مجموع الزوايا و.

على الرغم من الافتقار التام للدقة في صياغتنا، إلا أنها صحيحة، علاوة على ذلك، فهي مقبولة دائمًا من قبل ممتحني امتحان الدولة الموحدة. يجب عليك كتابة شيء مثل هذا:

"- منقوش" - وكل شيء سيكون على ما يرام!

لا تنس هذه العلامة المهمة - تذكر الصورة، وربما ستلفت انتباهك في الوقت المناسب عند حل المشكلة.

رباعي منقوش. وصف موجز والصيغ الأساسية

إذا كان الشكل الرباعي محصورا في دائرة، فإن مجموع أي زاويتين متقابلتين له يساوي

والعكس صحيح:

إذا كان الشكل الرباعي له زاويتان متقابلتان مجموعهما متساو، فإن الشكل الرباعي يكون دائريًا.

يكون الشكل الرباعي محصوراً في دائرة إذا وفقط إذا كان مجموع زاويته المتقابلتين متساوياً.

متوازي الأضلاع منقوش في دائرة- بالتأكيد مستطيل، ويتزامن مركز الدائرة مع نقطة تقاطع الأقطار.

شبه المنحرف المدرج في دائرة هو متساوي الساقين.

الشكل الرباعي منقوش في دائرة (مشاكل). نواصل النظر في المهام المدرجة في امتحان الدولة الموحدة في الرياضيات. في هذه المقالة سوف نقوم بحل العديد من المسائل باستخدام خصائص الزاوية المحيطية. لقد تم بالفعل توضيح النظرية بالتفصيل. في هذه المقالة، كان حل المشكلات يتلخص بشكل أساسي في تطبيق خاصية الزاوية المحيطية على الفور، أي أن هذه كانت مهام في إجراء واحد تقريبًا. هنا عليك أن تفكر قليلاً؛ إن مسار القرار ليس واضحاً دائماً على الفور.

ينطبق: نظرية مجموع زوايا المثلث، خصائص الزاوية المحيطية، خاصية الشكل الرباعي المحصور في دائرة. المزيد عن هذا الأخير.

*لقد تم عرض هذه الخاصية من قبل، ولكن بتفسير مختلف. لذا:

ملكيات:

الشكل الرباعي المنقوش هو شكل رباعي تقع رؤوسه جميعها على نفس الدائرة.
يمكن رسم شكل رباعي في دائرة إذا وفقط إذا كان مجموع زواياه المقابلة يساوي 180 درجة.

أي أننا إذا كنا شكلًا رباعيًا، فإن مجموع قياسات الزوايا المتقابلة له يساوي 180 درجة.

دعونا نفكر في المهام:

27870. في دائرة مركزها يا تيار متردد.و دينار بحريني- أقطار. الزاوية المركزية AODيساوي 1100 أوجد الزاوية المحيطية ايه سي بي. اكتب إجابتك بالدرجات.

مثلث بنظام التشغيلمتساوي الساقين، لأن نظام التشغيل=OB(هذه أنصاف الأقطار). ومن المعروف أن مجموع زوايا المثلث هو 180 درجة. خذ بعين الاعتبار ∠BOC و∠AOD:

لذلك

أي أن الزوايا الموجودة عند قاعدة المثلث متساوي الساقين متساوية

طريق اخر:

الزاوية AOB هي الزاوية المركزية للزاوية المحيطية ACB.بخاصية الزاوية الموضحة في الدائرة

مجموع الزوايا المجاورة هو 180 0، وهو ما يعني

هكذا

الجواب: 35

27871. الزاوية A للشكل الرباعي ABCD المدرج في دائرة تساوي 58 0. أوجد الزاوية C لهذا الشكل الرباعي. اكتب إجابتك بالدرجات.

ويكفي هنا أن نتذكر خاصية هذا الشكل الرباعي. ومن المعلوم أن مجموع قياسات الزوايا المتقابلة لها يساوي 180 درجة، أي أن الزاوية C ستكون مساوية لـ

الطريقة الثانية:

دعونا نبني OB وOD.

من خلال خاصية الزاوية المحيطية، فإن درجة حجم القوس BCD تساوي

2∙58 0 = 116 0

وبالتالي فإن درجة حجم القوس BAD ستكون مساوية لـ

360 0 – 116 0 = 244 0

وفقًا لخاصية الزاوية المحيطية، ستكون الزاوية C أصغر مرتين، أي 122 0.

الجواب: 122

27872. جوانب الشكل الرباعي ا ب ت ث أ.ب, قبل الميلاد, قرص مضغوطو إعلانتقابل أقواس الدائرة المقيدة، وقيم درجاتها هي على التوالي 95 0، 49 0، 71 0، 145 0. أوجد الزاوية بهذا الرباعي. اكتب إجابتك بالدرجات.

دعونا نبني نصف القطر AO، OD، OC:

قيمة درجة القوس AD تساوي 145 0، وقيمة درجة القوس CD تساوي 71 0، مما يعني أن قيمة درجة القوس ADC تساوي 145 0 + 71 0 = 216 0.

وفقًا لخاصية الزاوية المحيطية، ستكون الزاوية B نصف الزاوية المركزية المقابلة للقوس ADC، أي

الجواب: 108

27874. رباعي الزوايا ا ب ت ثمكتوب في دائرة. ركن اي بي سييساوي 1050 زاوية نذل - وغديساوي 35 0 . أوجد الزاوية عبد. اكتب إجابتك بالدرجات.

يمكن أن تكون هذه المهمة صعبة. من المستحيل على الفور رؤية التقدم المحرز في القرار بوضوح. دعونا نتذكر ما هو معروف عن الشكل الرباعي المنقوش: مجموع زواياه المتقابلة يساوي 180 درجة. دعونا نجد

لقد وجدنا حاليًا الزاوية التي يمكن تحديدها فورًا باستخدام خاصية معروفة. إذا كان من الممكن العثور على أي قيمة، فافعل ذلك، فسيكون ذلك مفيدًا. نحن نتصرف وفقًا لمبدأ "العثور على ما يمكن العثور عليه بناءً على قيم معينة".

الزاويتان المحيطيتان ABD وACD مبنيتان على نفس القوس، وهذا يعني أنهما متساويتان، أي

الجواب: 70

27875. رباعي الزوايا ا ب ت ثمكتوب في دائرة. ركن عبديساوي 75 0 زاوية نذل - وغديساوي 35 0 . أوجد الزاوية اي بي سي. اكتب إجابتك بالدرجات.

ومن المعلوم أن الزوايا المحيطية المبنية على نفس القوس وتلك الواقعة على نفس الجانب منه متساوية. لذلك

في المثلث ACD هناك زاويتان معروفتان، يمكننا إيجاد الثالثة:

ألاحظ أنه من المهم أن تتذكر الخصائص والمهام المحددة التي ستحلها دون مشاكل. وبطبيعة الحال، من الممكن بناء حل ليس صحيحا تماما. على سبيل المثال، في المشكلة رقم 27876، يتم تقديم حل "طويل" أو، كما يقولون أيضًا، غير منطقي للحل المستقل. لا بأس إذا قمت بحل المشكلة بنفس الطريقة.

الشيء الرئيسي هو أن تتذكر النظرية وتطبقها، وفي النهاية تحل المهمة.

في هذا القسم، سنستمر في النظر في المهام، أدعوك إلى المدونة!

هذا كل شئ. كل التوفيق لك!

مع أطيب التحيات، ألكسندر كروتيتسكيخ

اللجنة تسأل مدير مدرسة ريفية بسيطة:
- لأي سبب يقول كل أطفالك: عندما يأتون، عندما يذهبون؟
"من يدري، ربما هم معتادون على ذلك!"

ملاحظة: سأكون ممتنًا لو أخبرتني عن الموقع على الشبكات الاجتماعية.

المضلعات المنقوشة والدائرية،

§ 106. خصائص الرباعيات المدرجة والموصوفة.

النظرية 1. مجموع الزوايا المتقابلة في الشكل الرباعي الدائري هو 180 درجة.

دع الشكل الرباعي ABCD يُدرج في دائرة مركزها O (الشكل 412). مطلوب إثبات ذلك / أ+ / ج = 180 درجة و / ب + / د = 180 درجة.

/ A، كما هو مكتوب في الدائرة O، يبلغ قياسه 1/2 BCD.
/ C، كما هو مكتوب في نفس الدائرة، يبلغ قياسه 1/2 BAD.

وبالتالي، يتم قياس مجموع الزوايا A وC بنصف مجموع الأقواس BCD وBAD؛ في المجموع، تشكل هذه الأقواس دائرة، أي أن لها 360 درجة.
من هنا / أ+ / ج = 360 درجة: 2 = 180 درجة.

وكذا ثبت ذلك / ب + / د = 180 درجة. ومع ذلك، يمكن استنتاج ذلك بطريقة أخرى. نحن نعلم أن مجموع الزوايا الداخلية للشكل الرباعي المحدب هو 360 درجة. مجموع الزاويتين A وC يساوي 180 درجة، مما يعني أن مجموع الزاويتين الأخريين في الشكل الرباعي يظل أيضًا 180 درجة.

النظرية 2(يعكس). إذا كان في شكل رباعي فإن مجموع زاويتين متقابلتين متساوي 180 درجة ، فيمكن وصف دائرة حول هذا الشكل الرباعي.

ليكن مجموع الزوايا المتقابلة للشكل الرباعي ABCD يساوي 180 درجة، أي
/ أ+ / ج = 180 درجة و / ب + / د = 180 درجة (الرسم 412).

دعونا نثبت أنه يمكن وصف الدائرة حول هذا الشكل الرباعي.

دليل. من خلال أي من القمم الثلاثة لهذا الشكل الرباعي، يمكنك رسم دائرة، على سبيل المثال، من خلال النقاط A وB وC. أين تقع النقطة D؟

يمكن للنقطة D أن تأخذ أحد المواضع الثلاثة التالية فقط: أن تكون داخل الدائرة، وتكون خارج الدائرة، وتكون على محيط الدائرة.

لنفترض أن الرأس يقع داخل الدائرة ويأخذ الموضع D" (الشكل 413). ثم في الشكل الرباعي ABCD" سيكون لدينا:

/ ب + / د" = 2 د.

بمواصلة الجانب AD" إلى التقاطع مع الدائرة عند النقطة E ونقطتي التوصيل E و C، نحصل على الشكل الرباعي الدائري ABCE، والذي، من خلال النظرية المباشرة

/ ب+ / ه = 2 د.

ويترتب على هاتين المساويتين:

/ د" = 2 د - / ب؛
/ ه = 2 د - / ب؛

/ د" = / ه،

ولكن هذا لا يمكن أن يكون، لأنه / D"، كونها خارجية بالنسبة للمثلث CD"E، يجب أن تكون أكبر من الزاوية E. لذلك، لا يمكن أن تكون النقطة D داخل الدائرة.

وثبت أيضًا أن الرأس D لا يمكنه أن يأخذ الموضع D" خارج الدائرة (الشكل 414).

ويبقى أن ندرك أن الرأس D يجب أن يقع على محيط الدائرة، أي يتزامن مع النقطة E، مما يعني أنه يمكن وصف الدائرة حول الشكل الرباعي ABCD.

عواقب. 1. يمكن وصف الدائرة حول أي مستطيل.

2. يمكن وصف الدائرة حول شبه منحرف متساوي الساقين.

وفي كلتا الحالتين، مجموع الزوايا المتقابلة هو 180 درجة.

النظرية 3.في الشكل الرباعي المحدود مجموع الأضلاع المتقابلة متساوي. دع الشكل الرباعي ABCD يوصف حول دائرة (الرسم 415)، أي أن أضلاعه AB وBC وCD وDA مماسة لهذه الدائرة.

ويشترط إثبات أن AB + CD = AD + BC. دعونا نشير إلى نقاط التماس بالأحرف M، N، K، P. واستناداً إلى خصائص المماسات المرسومة للدائرة من نقطة واحدة (§ 75)، لدينا:

ع = أك؛
VR = VM؛
الاسم المميز = DK؛
CN = سم.

دعونا نضيف هذه المساواة مصطلحا بعد مصطلح. نحن نحصل:

AR + BP + DN + CN = AK + VM + DK + SM،

أي AB + CD = AD + BC، وهو ما يحتاج إلى إثبات.

تمارين.

1. في الشكل الرباعي الدائري، هناك زاويتان متقابلتان بنسبة 3:5.
والاثنان الآخران بنسبة 4:5 حدد مقدار هذه الزوايا.

2. في الشكل الرباعي الموصوف، مجموع الضلعين المتقابلين هو 45 سم، والضلعان المتبقيان بنسبة 0.2: 0.3. أوجد طول هذه الجوانب.

المجموع:0
في تواصل مع 0
جوجل+ 0
نعم 0
فيسبوك 0