Relazioni binarie, proprietà delle relazioni. Relazioni di equivalenza, ordine e tolleranza

Definizioni correlate

L'insieme di tutte le classi di equivalenza è indicato con .

Esempi di relazioni di equivalenza

Un esempio più complicato, ma assolutamente vitale:

Quando un medico ti prescrive un medicinale, infatti, indica nella ricetta la classe dei farmaci equivalenti, non può indicare un'istanza del tutto specifica della confezione di compresse o fiale. Quelli. tutti i tipi di farmaci sono divisi in classi da una relazione di equivalenza. Senza questo fatto, la medicina moderna semplicemente non sarebbe possibile.

Pertanto, tutti i tipi di ricette per insalate e cocktail, GOST e classificatori definiscono anche relazioni di equivalenza vitali. Le relazioni di equivalenza riempiono tutta la nostra vita e non sono un astratto passatempo dei matematici.

Fattorizzazione delle mappature

L'insieme delle classi di equivalenza corrispondenti alla relazione di equivalenza è indicato dal simbolo e viene chiamato insieme di fattori relativamente. In questo caso, la mappatura suriettiva

chiamato esposizione naturale(O proiezione canonica) sul quoziente impostato .

Sia , - sets, - mapping, quindi la relazione binaria definita dalla regola

è una relazione di equivalenza su . In questo caso, la mappatura induce la mappatura definita dalla regola

oppure, che è lo stesso,

Questo risulta in fattorizzazione trasformazioni in una mappatura suriettiva e una mappatura iniettiva.

La fattorizzazione della visualizzazione è ampiamente utilizzata nelle discipline umanistiche e in quelle aree della tecnologia dove non è possibile utilizzare valori numerici. La fattorizzazione della mappatura consente di rinunciare alle formule laddove le formule non possono essere applicate. Facciamo un esempio che sarà chiaro a chiunque e non richiede la comprensione del simbolismo matematico complesso.

L'orario scolastico è un tipico esempio di fattorizzazione. In questo caso l'insieme di tutti gli alunni della scuola è l'insieme di tutte le materie scolastiche, separate per giorni della settimana con la specificazione dell'orario delle lezioni. Le classi di equivalenza sono classi (gruppi di studenti). Visualizzazione: l'orario delle lezioni visualizzato nei diari degli studenti. Display - l'orario delle lezioni per classe, affisso nell'atrio della scuola. C'è anche un display: elenchi di classi. Questo esempio dimostra molto chiaramente i vantaggi pratici della fattorizzazione: è impossibile pensare a un orario di lezione come a una tabella che riflette tutti gli studenti di una scuola in ordine personale. La fattorizzazione ha permesso di visualizzare le informazioni necessarie agli studenti in una forma compatta, comoda da utilizzare in una situazione in cui non è possibile applicare le formule.

I vantaggi della fattorizzazione, però, non si limitano a questo. La fattorizzazione ha permesso di effettuare una divisione del lavoro tra i partecipanti all'attività: il dirigente scolastico redige un programma e gli studenti lo scrivono nei loro diari. Allo stesso modo, la fattorizzazione della prescrizione ha consentito una divisione del lavoro tra il medico che fa la diagnosi e scrive la prescrizione, e il farmacista che garantisce l’equivalenza dei farmaci prescritti. L'apoteosi della fattorizzazione è il trasportatore, che implementa la massima divisione del lavoro grazie alla standardizzazione delle parti.

Ma i vantaggi della fattorizzazione non si limitano a questo. La fattorizzazione ha permesso di garantire la modularità della tecnologia moderna, che le conferisce una flessibilità di funzioni senza precedenti. Puoi conservare la tua vecchia scheda SIM e acquistare un nuovo telefono oppure inserire una nuova memoria video nel vecchio computer. Tutto questo è flessibilità, modularità, che si basa sulla fattorizzazione.

Letteratura

A. I. Kostrikin, Introduzione all'algebra. M.: Nauka, 1977, 47-51.
A. I. Maltsev, Sistemi algebrici, M.: Nauka, 1970, 23-30.
V. V. Ivanov, Analisi matematica. NSU, 2009.

Guarda anche

La relazione di tolleranza è una forma indebolita di equivalenza.
L'equivalenza è un'operazione logica.

Fondazione Wikimedia. 2010 .

polmonite ospedaliera
Mitel

Scopri cos'è la "relazione di equivalenza" in altri dizionari:

relazione di equivalenza- - Argomenti delle telecomunicazioni, concetti di base Relazione di equivalenza EN ... Manuale del traduttore tecnico

Rapporto di uguaglianza- relazione di equivalenza, concetto di logica e matematica, che esprime il fatto che oggetti diversi hanno le stesse caratteristiche (proprietà). Rispetto a tali caratteristiche comuni, questi vari oggetti sono indistinguibili (identici, uguali, ... ...

Atteggiamento di tolleranza- Questo termine ha altri significati, vedi Tolleranza. Una relazione di tolleranza (o semplicemente tolleranza) su un insieme è una relazione binaria che soddisfa le proprietà di riflessività e simmetria, ma non necessariamente ... ... Wikipedia

Relazione (matematica)- Questo termine ha altri significati, vedi Atteggiamento. Una relazione è una struttura matematica che definisce formalmente le proprietà di vari oggetti e le loro relazioni. Le relazioni sono solitamente classificate in base al numero di oggetti che collegano... Wikipedia

ATTEGGIAMENTO- in logica, ciò che, a differenza di una proprietà, caratterizza non un oggetto separato, ma una coppia, una tripla, ecc. elementi. La logica tradizionale non considerava O.; nella logica moderna O. è una funzione proposizionale di due o più variabili. Binario… Enciclopedia filosofica

relazione di preferenza- nella teoria del consumo, questa è una descrizione formale della capacità del consumatore di confrontare (ordinare in base alla desiderabilità) diversi insiemi di beni (insiemi di consumatori). Per descrivere una relazione di preferenza, non è necessario misurare la desiderabilità... ...Wikipedia

Atteggiamento (filosofico)- Atteggiamento, una categoria filosofica che esprime la natura della posizione degli elementi di un particolare sistema e la loro interdipendenza; atteggiamento emotivamente volitivo dell'individuo verso qualcosa, cioè l'espressione della sua posizione; confronto mentale di vari oggetti ... ... Grande Enciclopedia Sovietica

atteggiamento- RELAZIONE insieme di n ok individui ordinati (dove n 1), ovvero due, tre, ecc. Il numero n è chiamato "località", o "arietà", O. e, di conseguenza, parlano di n locale (p arny) O. Quindi, ad esempio, O. a due posti si chiama ... ... Enciclopedia di epistemologia e filosofia della scienza

Atteggiamento- I L'atteggiamento è una categoria filosofica che esprime la natura della posizione degli elementi di un determinato sistema e la loro interdipendenza; atteggiamento emotivamente volitivo dell'individuo verso qualcosa, cioè l'espressione della sua posizione; confronto mentale di vari ... ... Grande Enciclopedia Sovietica

Classe di equivalenza- La relazione di equivalenza () sull'insieme X è una relazione binaria per la quale sono soddisfatte le seguenti condizioni: Riflessività: per qualsiasi a in X, Simmetria: se, allora, Transitività: se ... Wikipedia

Libri

Prendere decisioni finanziarie in condizioni di incertezza comparativa: monografia, Bayuk O.A. Nella monografia, una nuova strategia decisionale logica viene sviluppata e teoricamente motivata quando si sceglie tra oggetti incomparabili, stabilendo una speciale relazione di preferenza e ...

Lezione 22

1. Relazione di equivalenza. Collegamento della relazione di equivalenza con la divisione di un insieme in classi.

2. Rapporto d'ordine. Relazioni d'ordine strette e non strette, relazione d'ordine lineare. Ordinazione dei set.

3. Risultati chiave

Consideriamo l'insieme delle frazioni X= (1/2, 1/3, 1/4, 2/4, 2/6, 3/6) relazione di uguaglianza. Questa relazione:

Riflessivamente, poiché ogni frazione è uguale a se stessa;

È simmetrico, poiché dal fatto che la frazione M/N uguale ad una frazione P/Q, ne consegue che la frazione P/Q uguale ad una frazione M/N;

Transitivo, poiché dal fatto che la frazione M/N uguale ad una frazione P/Q e frazione P/Q uguale ad una frazione R/S, ne consegue che la frazione M/N uguale ad una frazione R/S.

Si dice che la relazione di uguaglianza delle frazioni sia relazione di equivalenza.

Definizione. Una relazione R su un insieme X è detta relazione di equivalenza se possiede contemporaneamente le proprietà di riflessività, simmetria e transitività.

Esempi di relazioni di equivalenza sono le relazioni di uguaglianza delle figure geometriche, la relazione di parallelismo delle rette (a condizione che le rette coincidenti siano considerate parallele).

Perché questo tipo di relazione viene individuato in matematica? Considera la relazione di uguaglianza delle frazioni fornite sull'insieme X= (1/2, 1/3, 1/4, 2/4, 2/6, 3/6) (fig. 106). Vediamo che l'insieme è diviso in tre sottoinsiemi: (1/2, 2/4, 3/6), (1/3, 2/6), (1/4). Questi sottoinsiemi non si intersecano e la loro unione coincide con l'insieme X, quelli. abbiamo una partizione del set X alle lezioni. Questa non è una coincidenza.

Affatto, se una relazione di equivalenza è data su un insieme X, allora genera una partizione di questo insieme in sottoinsiemi disgiunti a due a due (classi di equivalenza).

Quindi, abbiamo stabilito che la relazione di uguaglianza sull'insieme delle frazioni (1/2, 1/3, 1/4, 2/4, 2/6, 3/6) corrisponde alla partizione di questo insieme in classi di equivalenza, ciascuno dei quali è costituito da frazioni uguali tra loro.

È vero anche il contrario: se qualsiasi relazione data su un insieme X genera una partizione di questo insieme in classi, allora è una relazione di equivalenza.

Consideriamo, ad esempio, il set X=(1, 2, 3, 4, 5, 6, 7, 8, 9, 10) relazione "hanno lo stesso resto quando diviso per 3". Genera una partizione del set X in classi: una includerà tutti i numeri, quando diviso per 3, il resto è 0 (questi sono i numeri 3, 6, 9), il secondo - numeri, quando diviso per 3, il resto è 1 (questi sono i numeri 1 , 4, 7 , 10), e nel terzo - tutti i numeri, se divisi per 3, il resto è 2 (questi sono i numeri 2, 5, 8). Infatti i sottoinsiemi ottenuti non si intersecano e la loro unione coincide con l'insieme X. Pertanto, la relazione "ha lo stesso resto quando divisa per 3", fornita nel set X,è una relazione di equivalenza. Si noti che l'affermazione sulla relazione tra la relazione di equivalenza e la divisione di un insieme in classi necessita di essere dimostrata. Lo stiamo abbandonando. Diremo solo che se una relazione di equivalenza ha un nome, alle classi viene dato il nome corrispondente. Ad esempio, se su un insieme di segmenti è specificata una relazione di uguaglianza (ed è una relazione di equivalenza), allora l'insieme di segmenti viene diviso in classi di segmenti uguali (vedi Fig. 99). La relazione di similarità corrisponde alla divisione dell'insieme dei triangoli in classi di triangoli simili.

Quindi, avendo una relazione di equivalenza su un certo insieme, possiamo dividere questo insieme in classi. Ma si può anche fare il contrario: prima dividere l'insieme in classi, e poi definire una relazione di equivalenza, assumendo che due elementi siano equivalenti se e solo se appartengono alla stessa classe della partizione in esame.

Il principio di dividere un insieme in classi mediante una qualche relazione di equivalenza è un principio importante della matematica. Perché?

Innanzitutto, equivalente - significa equivalente, intercambiabile. Pertanto, gli elementi della stessa classe di equivalenza sono intercambiabili. Quindi, le frazioni che si trovano nella stessa classe di equivalenza (1/2, 2/4, 3/6) sono indistinguibili dal punto di vista della relazione di uguaglianza e la frazione 3/6 può essere sostituita con un'altra, ad esempio, 1/2. E questa sostituzione non cambierà il risultato dei calcoli.

In secondo luogo, poiché nella classe di equivalenza ci sono elementi indistinguibili dal punto di vista di qualche relazione, si ritiene che la classe di equivalenza sia determinata da uno qualsiasi dei suoi rappresentanti, ad es. elemento arbitrario di questa classe. Pertanto, qualsiasi classe di frazioni uguali può essere specificata specificando qualsiasi frazione appartenente a questa classe. La definizione di una classe di equivalenza da parte di un rappresentante consente, invece di tutti gli elementi dell'insieme, di studiare l'insieme dei singoli rappresentanti delle classi di equivalenza. Ad esempio, la relazione di equivalenza "avere lo stesso numero di vertici" data su un insieme di poligoni genera una partizione di questo insieme in classi di triangoli, quadrangoli, pentagoni e così via. Le proprietà inerenti a una determinata classe sono considerate su uno dei suoi rappresentanti.

Terzo, la divisione di un insieme in classi mediante una relazione di equivalenza viene utilizzata per introdurre nuovi concetti. Ad esempio, il concetto di "un fascio di linee" può essere definito come la cosa comune che hanno le linee parallele.

In generale, qualsiasi concetto con cui una persona opera rappresenta una certa classe di equivalenza. "Tavolo", "casa", "libro": tutti questi concetti sono idee generalizzate su una varietà di oggetti specifici che hanno lo stesso scopo.

Un altro tipo importante di relazione è rapporti d'ordine.

Definizione. Una relazione R su un insieme X è detta relazione d'ordine se possiede contemporaneamente le proprietà di antisimmetria e transitività .

Esempi di relazioni d'ordine sono: la relazione "minore di" sull'insieme dei numeri naturali; la relazione è "più breve" sull'insieme dei segmenti, poiché sono antisimmetrici e transitivi.

Se una relazione d'ordine possiede anche la proprietà di connessione, allora si dice che sia una relazione ordine lineare.

Ad esempio, la relazione "minore di" sull'insieme dei numeri naturali è una relazione di ordine lineare, poiché ha le proprietà di antisimmetria, transitività e connessione.

Definizione. Un insieme X si dice ordinato se su di esso è definita una relazione d'ordine.

Quindi, l'insieme N dei numeri naturali può essere ordinato se poniamo su di esso la relazione "minore di".

Se la relazione d'ordine definita sul set X, ha la proprietà connessa, lo diciamo ordina linearmente un mucchio di X.

Ad esempio, l'insieme dei numeri naturali può essere ordinato sia utilizzando la relazione "minore di" sia utilizzando la relazione "moltiplica" - entrambe sono relazioni di ordine. Ma la relazione “minore di”, a differenza della relazione “moltiplicatore”, ha anche la proprietà di essere connessa. Quindi, la relazione "minore di" ordina linearmente l'insieme dei numeri naturali.

Non si deve pensare che tutte le relazioni si dividano in relazioni di equivalenza e relazioni d'ordine. Esiste un numero enorme di relazioni che non sono né relazioni di equivalenza né relazioni di ordine.

In molti problemi computazionali, insiemi di grandi dimensioni vengono presi e partizionati in modo tale che tutte le situazioni di nostro interesse possano essere esplorate utilizzando pochi esempi ben scelti.

Definizione 1: Sia A ¹ Æ e (A i ),i= l'insieme dei sottoinsiemi tali che A= . Quindi viene chiamato l'insieme di questi sottoinsiemi rivestito imposta A.

Ad esempio, (A, B) è una copertura di AÈB; (A, AÈB, B, C)-rivestimento di AÈBÈC.

Commento: Nel caso generale la copertura può essere infinita. tuttavia, dal punto di vista dello studio delle proprietà specifiche, questa situazione non suscita entusiasmo.

Definizione 2: scissione di un insieme non vuoto A è detto suo ricoprimento tale che se i¹ j, allora A i ÇA j =Æ.

Ad esempio, (A, A') è una partizione U.

(AÇB, AÇB’, A’ÇB, A’ÇB’) – partizione U,

(A\B, AÇB, B\A) è una partizione di AÈB.

Puoi organizzare una partizione di un insieme non vuoto utilizzando relazioni che si comportano come relazioni di uguaglianza su un insieme di numeri o insiemi.

Definizione 3: Viene chiamata una relazione binaria su un insieme relazione di equivalenza, se è riflessiva, simmetrica e transitiva.

Esempi:

1. Sull'insieme di tutti i triangoli: ((x, y)| xey hanno la stessa area)

2. Sull'insieme di tutti i programmi: ((a, b)| a, b calcola la stessa funzione su una particolare macchina)

Definizione 4: Sia R una relazione di equivalenza su un insieme A e xОA. La classe di equivalenza generata dall'elemento x l'insieme si chiama (y| xR y)=[x] R .

Definizione 5: Viene chiamato qualsiasi elemento della classe di equivalenza rappresentante questa classe. Sistema completo di rappresentanti viene chiamato un insieme di rappresentanti, uno per ciascuna classe.

Esempio 3:

N sono numeri naturali, s è un elemento fisso. SU Z la relazione è definita: r s = ((x, y)| x-y=ns, nн Z). Atteggiamento confronti modulo s (record: xºy(mod s)).

È facile verificare che il confronto modulo s è una relazione di equivalenza sull'insieme Z.

Sia, ad esempio, s=10. Poi:

= {11,21,-9,10 976 631,.... }

= {66,226,-24,... }

Infatti, ci sono solo 10 classi di equivalenza in questa relazione, e i numeri 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 formano sistema completo di rappresentanti. Vengono chiamate le classi di equivalenza rispetto a questa relazione di equivalenza classi di detrazione modulo s.

Definizione 6: fattore per insieme l'insieme A rispetto alla relazione di equivalenza R è l'insieme di tutte le classi di equivalenza rispetto a tale relazione ed è indicato con A/R.

L'insieme delle classi di residui modulo s è indicato con Zs.

Si verifica

Teorema (sul partizionamento): Sia R una relazione di equivalenza su un insieme non vuoto A. Allora l'insieme quoziente A/R è una partizione dell'insieme A.

Prova:

"xОA(xО[x] R). È necessario dimostrare che ogni elemento dell'insieme A appartiene esattamente a una classe. Cioè, dimostriamo che se le classi hanno almeno un elemento comune, allora coincidono. Sia cО [a] e cО [b] Sia xО[a], ma allora x R a, a R c, c R b Þ x R b (R è transitivo). ) Allo stesso modo [b] Ì [a].

Q.E.D.

Vale anche il contrario. Sia S una partizione di un insieme A e R s una relazione binaria su A, tale che: R=((x,y)ïx e y appartengono allo stesso elemento della partizione ), allora R , chiameremo– la relazione definita dalla partizione S.

Teorema (inversione): La relazione R su A, definita dalla partizione di S, è una relazione di equivalenza su A, dove A/R s = S. (da solo)

Esercizi:

1. Sia A un insieme finito. Quali relazioni di equivalenza danno il numero più grande e più piccolo di classi di equivalenza.

2. Se (A 1 , A 2 , ..., A n ) è una partizione di A e A è finito, allora .

Relazione d'ordine.

Dal concetto di uguaglianza (ad esempio, i numeri) nasce il concetto matematico di equivalenza. E dal concetto di disuguaglianza nasce un altro tipo di relazione, che si chiama relazione di ordine.

Definizione 1: Ordine parziale sull'insieme A è detta relazione binaria riflessiva, antisimmetrica e transitiva.

Un ordine parziale è una generalizzazione della relazione £ con R. Si può introdurre la nozione ordine rigoroso corrispondente alla relazione< на R. Отношение строгого порядка - только транзитивно(оно еще и антирефлексивно).

Se £ è dato, allora possiamo definire<: a

Verrà indicato l'insieme su cui è data la relazione d'ordine

(X, £) (o (X,<), если порядок строгий).

Definizione 2: Viene chiamato l'insieme su cui è data la relazione d'ordine parzialmente ordinato.

Esempio: A è un insieme. ( P (A),Í), è facile verificare che il rapporto Í è la relazione d'ordine su P (UN).

Definizione 3: Si chiama la relazione d'ordine R su A completare ( lineare ) ordine, se " x, yнA (xR y Ú yR x). L'insieme (A, R) si dice ordinato linearmente.

Esempi:

1. relazione £ su Rè una relazione di ordine completo. Così ( R,£) - ordinato linearmente.

2. e qui ( P (A),Í) non è ordinato linearmente

3. x£y Û y x sul set N non è un ordine completo

Definizione 4: sia (A, £) è un insieme parzialmente ordinato. L'elemento si chiama aОА più piccolo / più grande / in A se " xОA (a £ x) /x £ a /. L'elemento bОА si chiama minimo/massimo/ if " xнA (x£ a z x=a) /a £ x z a=x /.

Compito: Dimostrare che per un insieme ordinato linearmente i concetti di elemento più grande (più piccolo) e massimo (minimo) coincidono. Fornisci un esempio di un insieme parzialmente ordinato in cui non corrispondono.

Composizione delle relazioni

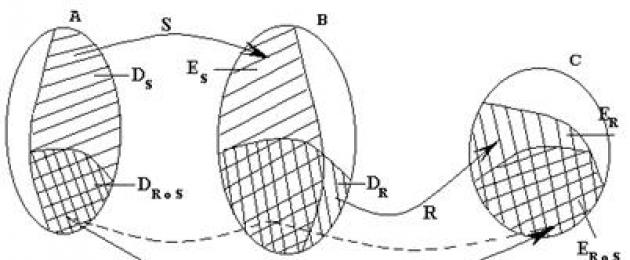
Siano dati gli insiemi A, B e C e le relazioni S tra A e B (cioè SÌA´B) e R tra B e C (RÌB´C). Definiamo una nuova relazione tra A e C come segue:

Definizione 1: L'insieme di tutte le coppie (x, y) tali che esista zнB tale che (x, z)í S e (z, y)í R si dice composizione delle relazioni S e R. Designato: R o S . Quindi, R o S М A ´ C .

R oS = ((x, y)| $zнB((x,z)нSu(z,y)нR)) oppure x R o Sy Û $zнB(xSzÙzRy).

Esempio 1 : Sia A=(1, 2, 3), B=(1, 2, 3, 4, 5, 6), C=(3, 6, 9, 12), s =((1,2), (2 .4), (3.6)), r=((1.3), (2.6), (3.9), (4.12)). Allora r o s=((1.6), (2.12)).

Illustriamo la situazione nella foto:

Esempio 2 : Sia s e r siano relazioni attive N tale che

S = ((x,x+1)íxí N) e r = ((x 2 ,x)íxí N). Allora D r = (x 2 ïxО N)=(1,4,9,16,25,...), e D s = N.

D r o s =(xïxО NÙ x+1=y 2 )=(3,8,15,24,...).

Nel caso in cui una relazione sia definita su un insieme, può essere combinata con se stessa:

sos = s 2 = ((x,x+2)½xí N) e ror = r 2 = ((x 4 ,x)½xн N}.

Usando questa notazione, si può definire l'ennesima potenza di una relazione:

, dove nО N,n>1.

Ad esempio, per le relazioni dell'esempio 2 abbiamo:

,

Vorrei integrare l'analogia con la moltiplicazione. Per fare ciò, introduciamo la seguente definizione naturale:

Definizione 2: Si chiamano relazioni binarie pari, se sono uguali come sottoinsiemi, cioè R=S se "x,y((x,y)íRw(x,y)íS).

È chiaro che le relazioni devono essere definite sugli stessi insiemi.

Teorema (proprietà della composizione della relazione): Per ogni relazione binaria R, S, T si verificano le uguaglianze:

1. (RoS)oT = Ro(SoT)

2. (RoS) -1 = S -1 o R -1

Prova:

1) Per ogni x e y abbiamo:

x(RoS)oTy º $z(xTzÙ(zRoSy)) º $z$t(xTzÙ(zStÙtRy)) º $z$t((xTzÙzSt)ÙtRy) º $t(($z(xTzÙzSt))ÙtRy) º $t((xSoTt)ÙtRy) º xRo(SoT)y.

2) x(RoS) -1 y º yRoSx º $z(ySzÙzRx) º $z(xR -1 zÙzS -1 y) º xS -1 oR -1 y.

Q.E.D.

Commento: se R è una relazione sull'insieme A, allora è chiaro che I A oR=RoI A =R. Cioè, I A si comporta come un'unità quando si moltiplicano i numeri. Tuttavia, non è possibile tracciare un’analogia completa. Poiché, ad esempio, la commutatività, nel caso generale, non c'è posto, poiché è possibile determinare RoS, ma SoR no. Anche l'uguaglianza R -1 oR=RoR -1 = I A non ha sempre senso.

Chiusura della relazione

Il concetto di chiusura è un concetto matematico fondamentale e viene utilizzato nella maggior parte dei rami della matematica. Illustriamo questo concetto con un esempio generale: prendiamo un oggetto x 0 e un processo P, che, applicato in sequenza, genera un certo insieme e, quindi, determina la sequenza x 1 , x 2 , ..., x n , . .. così che x 1 ОP(x 0), x 2 ОP(x 1),..., x n ОP(x n -1),...

Definizione 1: si chiama l'insieme contenente tutti gli elementi di tutte le sequenze ottenibili utilizzando il processo P e partendo da x 0 chiusura del processo P rispetto a x 0 .

È chiaro che il risultato sarà trovare P n (x 0) per alcuni N. Questo N non lo sappiamo in anticipo, dipende dal processo stesso. Inoltre, se prendiamo l'elemento sì da questa chiusura e applicare ad essa il processo R, non otterremo nulla di nuovo. Cioè, il set non può essere ampliato in questo modo: è chiuso!

Esempio : Prendiamo il quadrato S, etichettato ABCD, e consideriamo il processo r, che consiste nel ruotare il quadrato in senso orario di 90°:

La chiusura del processo r sarà un insieme composto da quattro posizioni:

Tuttavia, qualsiasi processo P può essere definito utilizzando una relazione binaria A=((x, y)| yнP(x), dove P è il processo in esame). Per costruire una chiusura della relazione A è sufficiente avere le relazioni A, A 2 , ..., A n e considerare l'unione di tutti gli elementi che si ottengono da x applicando A, A 2 , ..., A n, eccetera.
Sia data la relazione A su qualche insieme. Poi:

Definizione 2: chiusura transitiva la relazione A su un dato insieme è detta relazione A+ :

Pertanto, da una relazione non transitiva A su un certo insieme, si può costruire una relazione transitiva A + .

Esempi:

1. r - rapporto attivo N: r=((x, y)| y=x+1), allora r + =((x, y)| x
2.s avanti Q: s=((x, y)| x
3.t acceso Q: t=((x, y)| x×y=1), allora r + =((x, x)| x¹0)

4. Sia L l'insieme delle stazioni della metropolitana di Londra; L=(a, b, c) stazioni consecutive. N=((x, y)| y segue x). Quindi (a, b), (b, c) íN; inoltre, (a, a), (b, b), (c, c), (a, c) í N 2 . Quindi, N + =L´L

In generale, una chiusura transitiva non è riflessiva (Esempio 2).

Sia A una relazione su X. Sia A 0 =I X .

Definizione 3: Chiusura riflessiva A* la relazione A è detta relazione . Questo è .

Esempi:

1. r*=((x, y)| x£y)

Classi di elementi equivalenti e loro proprietà
Sia %%R%%. relazione di equivalenza sul set %%M%% e %%a%%, alcuni elementi di %%M%%. Considera l'insieme di tutti gli elementi di %%M%% che sono in relazione %%R%% con l'elemento %%a%%.

Classe di equivalenza%%M_a%%

si chiama l'insieme di tutti gli elementi %%M%% che sono in relazione %%R%% con l'elemento %%a%%, cioè l'insieme

$$ M_a = $x \in M: x~R~a$. $$

Esempio
Sia %%M%% l'insieme di tutti gli abitanti della Russia e %%R%% la relazione di equivalenza "vivere nella stessa città". Trova classi di elementi equivalenti %%M_a%% per %%a \in M%%.

La classe di elementi equivalente all'elemento %%a%% è: $$ M_a = $x \in M: x \text( vive nella stessa città della persona ) a$ $$

A seconda dell'elemento %%a%%, otteniamo diverse classi di equivalenza. Ad esempio, la classe di equivalenza dei residenti di Mosca o San Pietroburgo.

Proprietà delle classi di equivalenza
Sia %%R%% una relazione di equivalenza sull'insieme %%M%% e %%M_a, M_b, \dotsc, M_z, \dotsc%% siano tutte classi di equivalenza per la relazione %%R%%. Quindi queste classi hanno le seguenti proprietà.

Proprietà 1
Qualsiasi elemento %%a \in M%% soddisfa la condizione $$ a \in M_a $$

Infatti, per definizione, la classe %%M_a = $x \in M: x~R~a$%%. Allora l'elemento %%a%% deve soddisfare la condizione %%a \in M_a \leftrightarrow a~R~a%%, il che è vero perché la relazione %%R%% è riflessiva per definizione di una relazione di equivalenza. Pertanto, %%a \in M_a%%.

Di conseguenza di questa proprietà, possiamo dire che qualsiasi classe %%M_a%% è un insieme non vuoto.

Proprietà 2
Siano %%M_a%% e %%M_b%% le classi di equivalenza per la relazione %%R%%. Le classi %%M_a%% e %%M_b%% sono uguali se e solo se l'elemento %%a%% è in relazione %%R%% con l'elemento %%b%%. $$ M_a = M_b \leftrightarrow a~R~b. $$

Proprietà 3
Siano %%M_a%% e %%M_b%% le classi di equivalenza per la relazione %%R%%. Quindi le classi %%M_a%% e %%M_b%% non hanno elementi comuni. $$ M_a \neq M_b \rightarrow M_a \cap M_b = \varniente $$

Proprietà 4
L'unione di tutte le classi di equivalenza dell'insieme %%M%% è uguale all'insieme %%M%%. $$ \bigcup_(a\in M)(M_a) = M. $$

Imposta la partizione
L'insieme dei sottoinsiemi %%M_i%%, dove %%i \in I%% (all'insieme degli indici), viene chiamato l'insieme %%M%% scissione imposta %%M%% se sono soddisfatte le seguenti condizioni:

Ciascuno dei sottoinsiemi %%M_i%% non è vuoto.
L'unione di tutti i sottoinsiemi di %%M_i%% equivale all'insieme %%M%%.
Due sottoinsiemi diversi %%M_i%% e %%M_j%%, dove %%i \neq j%%, non hanno elementi comuni.

Teorema. Sia %%R%% una relazione di equivalenza sull'insieme %%M%%. Quindi l'insieme delle classi di equivalenza dell'insieme %%M%% forma la sua partizione.

Infatti, se prendiamo le classi di equivalenza %%M_a%% come sottoinsiemi di %%M_i%%, allora tutte e tre le condizioni sono soddisfatte:

Ogni classe di equivalenza è un insieme non vuoto, secondo proprietà 1.
L'unione di tutte le classi di equivalenza è l'insieme %%M%%, secondo proprietà 4.
Due diverse classi di equivalenza non hanno elementi comuni, secondo proprietà 3.

Tutte le condizioni di definizione della partizione sono soddisfatte. Quindi le classi di equivalenza sono una partizione dell'insieme %%M%%.

Esempi
Sia dato l'insieme %%M = $1, 2, 3, 4, 5, 6, 7, 8, 9, 0 $%% , quindi le seguenti raccolte di insiemi possono essere una partizione di questo insieme:

%%A_1 = $1, 2, 3$, A_2 = $4, 5, 6, 7$, A_3 = $8, 9, 0 $%%.
%%B_1 = $0, 7, 2$, B_2 = $1, 3, 5$, B_3 = $4, 6, 8, 9$%%.

Ma le seguenti raccolte non sono partizioni:

%%C_1 = $1, 2, 3$, C_2 = $4, 5, 6, 7$, C_3 = $8, 9, 0, 3$%%.
%%D_1 = $0, 7, 2$, D_2 = $1, 3, 5 $, D_3 = $4, 6, 8, 9$, D_4 = \varniente%%.
%%E_1 = $0, 1, 2$, Mi_2 = $3, 4, 5$, Mi_3 = $6, 7, 8$%%.

La raccolta di set %%C_i%% non è una partizione, perché non soddisfa la condizione 3 del partizionamento degli insiemi: gli insiemi %%C_1%% e %%C_3%% hanno un elemento comune %%3%%.

La raccolta di set %%D_i%% non è una partizione, perché non soddisfa la condizione 1 del partizionamento dell'insieme: l'insieme %%D_4%% è vuoto.

La raccolta di set %%E_i%% non è una partizione, perché non soddisfa la condizione di suddivisione dell'insieme 2: l'unione degli insiemi %%E_1, E_2%% e %%E_3%% non forma l'insieme %%M%%.

Annotazione: Vengono descritti molti nuovi concetti, come la relazione di equivalenza, la relazione di ordine parziale, gli insiemi parziali isomorfi. Diversi teoremi sull'argomento vengono dimostrati con spiegazioni dettagliate, grafici ed esempi. Viene fornito un gran numero di esempi di ordini parziali. Vengono descritte diverse costruzioni che consentono di costruire alcuni insiemi ordinati a partire da altri. La lezione è caratterizzata da molti compiti per una soluzione indipendente.
Relazioni di equivalenza e d'ordine
Richiama questo relazione binaria su un insieme si dice sottoinsieme; invece di scrivi spesso.
Viene chiamata una relazione binaria su un insieme relazione di equivalenza se sono vere le seguenti proprietà:
C'è la seguente affermazione ovvia ma spesso usata:
Teorema 11. (a) Se un insieme è partizionato in un'unione di sottoinsiemi disgiunti, allora la relazione "appartengono a un sottoinsieme" è una relazione di equivalenza.
(b) Qualsiasi cosa relazione di equivalenzaè ottenuto con il metodo descritto da qualche partizione.
Prova. La prima affermazione è abbastanza ovvia; diamo una dimostrazione della seconda, in modo che si possa vedere dove vengono utilizzati tutti i punti della definizione di equivalenza. Sia quindi una relazione di equivalenza. Per ogni elemento, consideralo classe di equivalenzaè l'insieme di tutti per i quali .
Dimostriamo che per due diversi insiemi tali o non si intersecano o coincidono. Lascia che si intersechino, cioè abbiano un elemento comune. Quindi e , da cui (simmetria) e (transitività), nonché (simmetria). Pertanto, per ognuno di essi segue (transitività) e viceversa.
Resta da notare che, in virtù della riflessività, ogni elemento appartiene alla classe che definisce, cioè l'intero insieme è infatti suddiviso in classi disgiunte.
78. Mostrare che i requisiti di simmetria e transitività possono essere sostituiti da uno: (mantenendo il requisito di riflessività).
79. Quante diverse relazioni di equivalenza esistono sul set ?
80. Ci sono due relazioni di equivalenza sull'insieme, indicate con e , aventi e classi di equivalenza, rispettivamente. La loro intersezione sarà una relazione di equivalenza? Quante lezioni può avere? Di cosa si può dire associazione di relazioni?
81. (Teorema di Ramsey) L'insieme di tutti i sottoinsiemi elementari di un insieme infinito è diviso in classi (, - numeri naturali). Dimostrare che esiste insieme infinito, i cui sottoinsiemi elementari appartengono tutti alla stessa classe.
(Questo è ovvio: se insieme infinito diviso in un numero finito di classi, allora una delle classi è infinita. Quando e l'affermazione può essere formulata come segue: da un insieme infinito di persone, si può scegliere un numero infinito di conoscenti a coppie o un numero infinito di estranei a coppie. La versione finale di questa affermazione - che tra sei persone ci sono tre coppie di conoscenti o tre coppie di sconosciuti - è un problema ben noto agli scolari.)
Viene chiamato l'insieme delle classi di equivalenza fattore - impostato insiemi sotto la relazione di equivalenza . (Se la relazione è coerente con strutture aggiuntive su , otteniamo gruppi di fattori, anelli di fattori, ecc.)
Incontreremo le relazioni di equivalenza più di una volta, ma ora il nostro argomento principale sono le relazioni di ordine.
Viene chiamata una relazione binaria su un insieme relazione d'ordine parziale se sono soddisfatte le seguenti proprietà:
(Seguendo la tradizione, usiamo un simbolo (piuttosto che una lettera) come segno di una relazione d'ordine.) Un insieme con una relazione d'ordine parziale definita su di esso è chiamato parzialmente ordinato.
Dicono che due elementi parzialmente ordinato imposta paragonabile, io per . Si noti che la definizione di ordine parziale non richiede che due elementi qualsiasi di un insieme siano comparabili. Aggiungendo questo requisito, otteniamo la definizione ordine lineare (insieme ordinato linearmente).
Ecco alcuni esempi di ordini parziali:
Insiemi numerici con la consueta relazione d'ordine (qui l'ordine sarà lineare).

Sull'insieme di tutte le coppie di numeri reali si può introdurre ordine parziale, assumendo che , se e . Quest'ordine non sarà più lineare: le coppie e non sono comparabili.

Sull'insieme delle funzioni con argomenti e valori reali, si può introdurre ordine parziale, supponendo che se con tutto . Questo ordine non sarà lineare.

Sull'insieme degli interi positivi, è possibile determinare l'ordine, assumendo che se divide . Anche questo ordine non sarà lineare.

La relazione "qualsiasi divisore primo di un numero è anche un divisore di un numero" non sarà una relazione d'ordine sull'insieme degli interi positivi (è riflessiva e transitiva, ma non antisimmetrica).

Sia un insieme arbitrario. Allora sull'insieme di tutti i sottoinsiemi dell'insieme la relazione di inclusione sarà un ordine parziale.

Sulle lettere dell'alfabeto russo, la tradizione definisce un certo ordine (). Questo ordine è lineare: per due lettere qualsiasi, puoi dire quale è la prima (se necessario, guardando nel dizionario).

Nelle parole dell'alfabeto russo è definito lessicografico ordine (come in un dizionario). Formalmente, può essere definito come segue: se la parola è l'inizio della parola, allora (ad esempio,). Se nessuna delle parole è l'inizio di un'altra, guarda la prima lettera in cui le parole differiscono: allora la parola dove questa lettera è minore in ordine alfabetico sarà minore. Anche questo ordine è lineare (altrimenti cosa farebbero i compilatori di dizionari?).

Anche la relazione di uguaglianza () lo è relazione d'ordine parziale, per il quale non sono comparabili due elementi distinti.

Facciamo ora un esempio domestico. Lascia che ci siano molte scatole di cartone. Introduciamo un ordine su di esso, assumendo che se la scatola si inserisce interamente all'interno della scatola (o se e sono la stessa scatola). A seconda dell'insieme di riquadri, questo ordine può essere lineare o meno.

totale:0

In contatto con 0

Google Plus 0

OK 0

Facebook 0