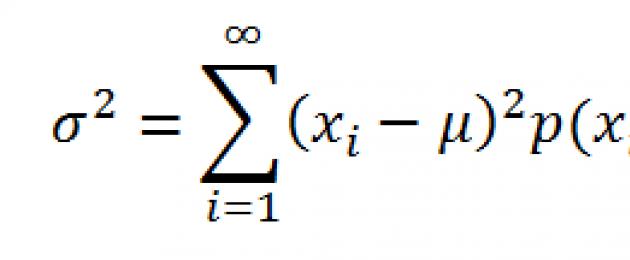Formula per il calcolo della varianza di una variabile casuale discreta. Tipi di dispersioni

CalcoliamoSMECCELLEREvarianza campionaria e deviazione standard. Calcoleremo anche la varianza di una variabile casuale se ne conosciamo la distribuzione.

Consideriamo prima dispersione, Poi deviazione standard.

Varianza di campionamento

Varianza di campionamento (varianza di campionamento,campionevarianza) caratterizza la diffusione dei valori nell'array rispetto a .

Tutte e 3 le formule sono matematicamente equivalenti.

Dalla prima formula è chiaro che varianza di campionamentoè la somma delle deviazioni al quadrato di ciascun valore nella matrice dalla media, diviso per la dimensione del campione meno 1.

varianze campioni viene utilizzata la funzione DISP(), inglese. il nome VAR, cioè Varianza. A partire dalla versione MS EXCEL 2010, si consiglia di utilizzare l'analogo DISP.V(), inglese. il nome VARS, cioè Varianza di campionamento. Inoltre, a partire dalla versione di MS EXCEL 2010, è disponibile la funzione DISP.Г(), in inglese. nome VARP, cioè Varianza della popolazione, che calcola dispersione Per popolazione. Tutta la differenza si riduce al denominatore: invece di n-1 come DISP.V(), DISP.G() ha solo n al denominatore. Prima di MS EXCEL 2010, la funzione VAR() veniva utilizzata per calcolare la varianza della popolazione.

Varianza di campionamento
=QUADROTCL(Campione)/(COUNT(Campione)-1)
=(SOMMA(Campione)-COUNT(Campione)*MEDIA(Campione)^2)/ (COUNT(Campione)-1)– formula abituale
=SOMMA((Campione -MEDIA(Campione))^2)/ (COUNT(Campione)-1) –

Varianza di campionamentoè uguale a 0, solo se tutti i valori sono uguali tra loro e, di conseguenza, uguali valore medio. Di solito, maggiore è il valore varianze, maggiore è la diffusione dei valori nell'array.

Varianza di campionamentoè una stima puntuale varianze distribuzione della variabile casuale da cui è stata ricavata campione. A proposito di costruzione intervalli di confidenza durante la valutazione varianze si può leggere nell'articolo.

Varianza di una variabile casuale

Calcolare dispersione variabile casuale, devi conoscerla.

Per varianze la variabile casuale X è spesso indicata con Var(X). Dispersione uguale al quadrato dello scostamento dalla media E(X): Var(X)=E[(X-E(X)) 2 ]

dispersione calcolato con la formula:

dove x i è il valore che può assumere una variabile casuale e μ è il valore medio (), p(x) è la probabilità che la variabile casuale assuma il valore x.

Se una variabile casuale ha , allora dispersione calcolato con la formula:

Dimensione varianze corrisponde al quadrato dell'unità di misura dei valori originali. Ad esempio, se i valori nel campione rappresentano le misurazioni del peso della parte (in kg), la dimensione della varianza sarebbe kg 2 . Questo può essere difficile da interpretare, quindi per caratterizzare la diffusione dei valori, un valore uguale alla radice quadrata di varianze – deviazione standard.

Alcune proprietà varianze:

Var(X+a)=Var(X), dove X è una variabile casuale e a è una costante.

Var(a×)=a 2 Var(X)

Var(X)=E[(X-E(X)) 2 ]=E=E(X 2)-E(2*X*E(X))+(E(X)) 2 =E(X 2)- 2*E(X)*E(X)+(E(X)) 2 =E(X 2)-(E(X)) 2

Questa proprietà di dispersione viene utilizzata in articolo sulla regressione lineare.

Var(X+Y)=Var(X) + Var(Y) + 2*Cov(X;Y), dove X e Y sono variabili casuali, Cov(X;Y) è la covarianza di queste variabili casuali.

Se le variabili casuali sono indipendenti, allora lo sono covarianzaè uguale a 0, e quindi Var(X+Y)=Var(X)+Var(Y). Questa proprietà di dispersione viene utilizzata nella derivazione.

Mostriamo che per quantità indipendenti Var(X-Y)=Var(X+Y). Infatti, Var(X-Y)= Var(X-Y)= Var(X+(-Y))= Var(X)+Var(-Y)= Var(X)+Var(-Y)= Var( X)+(- 1) 2 Var(Y)= Var(X)+Var(Y)= Var(X+Y). Questa proprietà di dispersione viene utilizzata per costruire .

Deviazione standard del campione

Deviazione standard del campioneè una misura di quanto sono sparsi i valori in un campione rispetto ai loro valori.

A priori, deviazione standard uguale alla radice quadrata di varianze:

Deviazione standard non tiene conto dell'entità dei valori in campione, ma solo il grado di dispersione dei valori attorno a loro media. Per illustrare ciò, diamo un esempio.

Calcoliamo la deviazione standard per 2 campioni: (1; 5; 9) e (1001; 1005; 1009). In entrambi i casi, s=4. È ovvio che il rapporto tra la deviazione standard e i valori dell'array differisce significativamente tra i campioni. Per questi casi viene utilizzato Il coefficiente di variazione(Coefficiente di variazione, CV) - rapporto Deviazione standard alla media aritmetica, espresso in percentuale.

In MS EXCEL 2007 e versioni precedenti per il calcolo Deviazione standard del campione viene utilizzata la funzione =STDEVAL(), inglese. nome DEV.ST, ad es. Deviazione standard. A partire dalla versione di MS EXCEL 2010 si consiglia di utilizzare l'analogo =STDEV.B() , inglese. nome DEV.ST.S, ovvero Esempio di deviazione standard.

Inoltre, a partire dalla versione di MS EXCEL 2010, è presente la funzione STANDARDEV.G(), inglese. nome DEV.ST.P, cioè Popolazione STandard DEViation, che calcola deviazione standard Per popolazione. Tutta la differenza si riduce al denominatore: invece di n-1 come in STANDARDEV.V(), STANDARDEVAL.G() ha solo n al denominatore.

Deviazione standard può anche essere calcolato direttamente utilizzando le formule seguenti (vedi file di esempio)
=ROOT(QUADROTCL(Campione)/(COUNT(Campione)-1))
=ROOT((SUM(Campione)-COUNT(Campione)*MEDIA(Campione)^2)/(COUNT(Campione)-1))

Altre misure di dispersione

La funzione SQUADROTCL() calcola con una somma dei quadrati delle deviazioni dei valori dai loro media. Questa funzione restituirà lo stesso risultato della formula =DISP.G( Campione)*CONTROLLO( Campione) , Dove Campione- un riferimento a un intervallo contenente un array di valori campione (). I calcoli nella funzione QUADROCL() vengono eseguiti secondo la formula:

La funzione SROTCL() è anche una misura della diffusione di un set di dati. La funzione SROTCL() calcola la media dei valori assoluti delle deviazioni dei valori da media. Questa funzione restituirà lo stesso risultato della formula =SUMPRODOTTO(ABS(Campione-MEDIA(Campione)))/COUNT(Campione), Dove Campione- un collegamento a un intervallo contenente una matrice di valori campione.

I calcoli nella funzione SROTCL () vengono effettuati secondo la formula:

Oltre a studiare la variazione di una caratteristica nell'intera popolazione, è spesso necessario tracciare i cambiamenti quantitativi nella caratteristica tra i gruppi in cui è divisa la popolazione, nonché tra i gruppi. Questo studio della variazione si ottiene calcolando e analizzando diversi tipi di varianza.
Esistono varianze totali, intergruppo e intragruppo.
Varianza totale σ 2 misura la variazione di un tratto nell'intera popolazione sotto l'influenza di tutti i fattori che hanno causato questa variazione.

La varianza intergruppo (δ) caratterizza la variazione sistematica, cioè differenze nel valore del tratto studiato che sorgono sotto l'influenza del tratto fattore che costituisce la base del gruppo. Si calcola utilizzando la formula:
.

Varianza all'interno del gruppo (σ) riflette la variazione casuale, cioè parte della variazione che avviene sotto l'influenza di fattori non contabilizzati e non dipende dal fattore-attributo che costituisce la base del gruppo. Si calcola con la formula:
.

Media delle varianze all'interno del gruppo: .

Esiste una legge che collega 3 tipi di dispersione. La varianza totale è pari alla somma della media della varianza intragruppo e tra gruppi: .
Questo rapporto è chiamato regola per aggiungere varianze.

Un indicatore ampiamente utilizzato nelle analisi è la proporzione della varianza tra gruppi nella varianza totale. È chiamato coefficiente empirico di determinazione (η 2): .
Viene chiamata la radice quadrata del coefficiente empirico di determinazione rapporto di correlazione empirica (η):
.
Caratterizza l'influenza della caratteristica che costituisce la base del gruppo sulla variazione della caratteristica risultante. Il rapporto di correlazione empirica varia da 0 a 1.
Dimostriamone l'uso pratico utilizzando il seguente esempio (Tabella 1).

Esempio n. 1. Tabella 1 - Produttività del lavoro di due gruppi di lavoratori in uno dei laboratori della NPO "Cyclone"

Calcoliamo le medie e le varianze complessive e di gruppo:

I dati iniziali per il calcolo della media della varianza intragruppo e intergruppo sono presentati nella tabella. 2.
Tavolo 2
Calcolo e δ 2 per due gruppi di lavoratori.

Gruppi di lavoratori	Numero di lavoratori, persone	Nella media, bambini/turno	Dispersione
Formazione tecnica completata	5	95	42,0
Coloro che non hanno completato la formazione tecnica	5	81	231,2
Tutti i lavoratori	10	88	185,6

Calcoliamo gli indicatori. Media delle varianze all'interno del gruppo:
.
Varianza intergruppo

Varianza totale:
Pertanto, il rapporto di correlazione empirica: .

Insieme alla variazione delle caratteristiche quantitative, si può osservare anche la variazione delle caratteristiche qualitative. Questo studio della variazione si ottiene calcolando i seguenti tipi di varianze:

La dispersione delle azioni all'interno del gruppo è determinata dalla formula

Dove no io– numero di unità in gruppi separati.
La quota della caratteristica studiata nell'intera popolazione, che è determinata dalla formula:
I tre tipi di varianza sono correlati tra loro come segue:
.

Questa relazione delle varianze è chiamata teorema dell'addizione delle varianze della condivisione dei tratti.

Tra i tanti indicatori utilizzati nelle statistiche è necessario evidenziare il calcolo della varianza. Va notato che eseguire questo calcolo manualmente è un compito piuttosto noioso. Fortunatamente Excel dispone di funzioni che consentono di automatizzare la procedura di calcolo. Scopriamo l'algoritmo per lavorare con questi strumenti.

La dispersione è un indicatore di variazione, ovvero il quadrato medio delle deviazioni dall'aspettativa matematica. Pertanto, esprime la diffusione dei numeri attorno al valore medio. Il calcolo della varianza può essere effettuato sia per la popolazione generale che per il campione.

Metodo 1: calcolo basato sulla popolazione

Per calcolare questo indicatore in Excel per la popolazione generale, utilizzare la funzione DISP.G. La sintassi di questa espressione è la seguente:

DISP.G(Numero1;Numero2;…)

In totale è possibile utilizzare da 1 a 255 argomenti. Gli argomenti possono essere valori numerici o riferimenti alle celle in cui sono contenuti.

Vediamo come calcolare questo valore per un intervallo con dati numerici.

Metodo 2: calcolo per campione

A differenza del calcolo di un valore basato su una popolazione, nel calcolo di un campione il denominatore non indica il numero totale di numeri, ma uno in meno. Questo viene fatto allo scopo di correggere gli errori. Excel tiene conto di questa sfumatura in una funzione speciale progettata per questo tipo di calcolo: DISP.V. La sua sintassi è rappresentata dalla seguente formula:

VIS.B(Numero1;Numero2;…)

Anche il numero di argomenti, come nella funzione precedente, può variare da 1 a 255.

Come puoi vedere, il programma Excel può facilitare notevolmente il calcolo della varianza. Questa statistica può essere calcolata dall'applicazione, sia dalla popolazione che dal campione. In questo caso, tutte le azioni dell'utente si riducono effettivamente alla specifica dell'intervallo di numeri da elaborare ed Excel svolge il lavoro principale da solo. Naturalmente, ciò farà risparmiare una notevole quantità di tempo all'utente.

Per dati raggruppati varianza residua- media degli scostamenti infragruppo:

Dove σ 2 j è la varianza intragruppo del jesimo gruppo.

Per dati non raggruppati varianza residua– misura della precisione di approssimazione, ovvero approssimazione della retta di regressione ai dati originali:
dove y(t) – previsione secondo l'equazione del trend; y t – serie dinamica iniziale; n – numero di punti; p – numero di coefficienti dell'equazione di regressione (numero di variabili esplicative).
In questo esempio si chiama stimatore imparziale della varianza.

Esempio n. 1. La distribuzione dei lavoratori di tre imprese di un'associazione secondo le categorie tariffarie è caratterizzata dai seguenti dati:

Categoria tariffaria del lavoratore	Numero di lavoratori dell'impresa
	impresa 1	impresa 2	impresa 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Definire:
1. scostamento per singola impresa (scostamento infragruppo);
2. la media degli scostamenti intragruppo;
3. dispersione intergruppo;
4. varianza totale.

Soluzione.
Prima di iniziare a risolvere il problema, è necessario scoprire quale caratteristica è efficace e quale è fattoriale. Nell'esempio in esame, l'attributo risultante è "Categoria tariffaria" e l'attributo fattore è "Numero (nome) dell'impresa".
Abbiamo poi tre gruppi (imprese), per i quali è necessario calcolare la media del gruppo e gli scostamenti intragruppo:

Azienda	Media del gruppo,	Varianza all'interno del gruppo,
1	4	1,8

La media delle varianze all'interno del gruppo ( varianza residua) sarà calcolato utilizzando la formula:

dove puoi calcolare:
O:

Poi:
La varianza totale sarà pari a: s 2 = 1,6 + 0 = 1,6.
La varianza totale può anche essere calcolata utilizzando una delle due formule seguenti:

Quando si risolvono problemi pratici, spesso si ha a che fare con una caratteristica che assume solo due valori alternativi. In questo caso non stiamo parlando del peso di un particolare valore di una caratteristica, ma della sua quota nella totalità. Se la proporzione di unità di popolazione che possiedono la caratteristica studiata è indicata con “ R", e quelli che non hanno - attraverso " Q", allora la varianza può essere calcolata utilizzando la formula:
s2 = p×q

Esempio n.2. Sulla base dei dati di produzione di sei lavoratori in una squadra, determinare la varianza intergruppo e valutare l'impatto del turno di lavoro sulla produttività del lavoro se la varianza totale è 12,2.

Collaboratore in squadra n.	Produzione del lavoratore, pz.
	nel primo turno	nel secondo turno
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Soluzione. Dati iniziali

X	f1	f2	f3	f4	f5	f6	Totale
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Totale	31	33	37	37	40	38

Quindi abbiamo 6 gruppi per i quali è necessario calcolare la media del gruppo e le varianze intragruppo.
1. Trova i valori medi di ciascun gruppo.







2. Trova il quadrato medio di ciascun gruppo.







Riassumiamo i risultati del calcolo in una tabella:

Numero del gruppo	Media del gruppo	Varianza all'interno del gruppo
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Varianza all'interno del gruppo caratterizza il cambiamento (variazione) della caratteristica studiata (risultata) all'interno di un gruppo sotto l'influenza di tutti i fattori su di esso, ad eccezione del fattore alla base del raggruppamento:
La media degli scostamenti infragruppo sarà calcolata utilizzando la formula:


4. Varianza intergruppo caratterizza il cambiamento (variazione) della caratteristica studiata (risultata) sotto l'influenza di un fattore (caratteristica fattoriale) che costituisce la base del gruppo.
Definiamo la varianza intergruppo come:

Dove


Poi

Varianza totale caratterizza il cambiamento (variazione) della caratteristica studiata (risultata) sotto l'influenza di tutti i fattori (caratteristiche fattoriali) senza eccezioni. Secondo le condizioni del problema, è pari a 12,2.
Relazione di correlazione empirica misura quale parte della variabilità totale della caratteristica risultante è causata dal fattore studiato. Questo è il rapporto tra la varianza del fattore e la varianza totale:

Definiamo la relazione di correlazione empirica:

Le connessioni tra le caratteristiche possono essere deboli e forti (strette). I loro criteri sono valutati sulla scala Chaddock:
0,1 0,3 0,5 0,7 0,9 Nel nostro esempio, la relazione tra tratto Y e fattore X è debole
Coefficiente di determinazione.

Determiniamo il coefficiente di determinazione:

Pertanto, lo 0,67% della variazione è dovuto a differenze tra i tratti e il 99,37% è dovuto ad altri fattori.
Conclusione: in questo caso, la produzione dei lavoratori non dipende dal lavoro svolto in un turno specifico, vale a dire l'influenza del turno di lavoro sulla produttività del lavoro non è significativa ed è dovuta ad altri fattori.

Esempio n.3. Sulla base dei dati sui salari medi e sulle deviazioni al quadrato dal suo valore per due gruppi di lavoratori, trovare la varianza totale applicando la regola di somma delle varianze:

Soluzione:
Media delle varianze all'interno del gruppo

Definiamo la varianza intergruppo come:


La varianza totale sarà: 480 + 13824 = 14304

I principali indicatori generalizzati di variazione nelle statistiche sono le dispersioni e le deviazioni standard.

Dispersione questo significato aritmetico deviazioni quadratiche di ciascun valore caratteristico dalla media complessiva. La varianza è solitamente chiamata valore quadratico medio delle deviazioni ed è indicata con  2. A seconda dei dati di origine, la varianza può essere calcolata utilizzando la media aritmetica semplice o ponderata:

 varianza non ponderata (semplice);

 varianza ponderata.

Deviazione standard questa è una caratteristica generalizzante delle dimensioni assolute variazioni segni in totale. È espresso nelle stesse unità di misura dell'attributo (in metri, tonnellate, percentuale, ettari, ecc.).

La deviazione standard è la radice quadrata della varianza ed è indicata con :

 deviazione standard non ponderata;

 deviazione standard ponderata.

La deviazione standard è una misura dell’affidabilità della media. Quanto più piccola è la deviazione standard, tanto meglio la media aritmetica riflette l'intera popolazione rappresentata.

Il calcolo della deviazione standard è preceduto dal calcolo della varianza.

La procedura per il calcolo della varianza ponderata è la seguente:

1) determinare la media aritmetica ponderata:

2) calcolare gli scostamenti delle opzioni dalla media:

3) eleva al quadrato la deviazione di ciascuna opzione dalla media:

4) moltiplicare i quadrati delle deviazioni per i pesi (frequenze):

5) riassumere i prodotti risultanti:

6) l'importo risultante viene diviso per la somma dei pesi:

Esempio 2.1

Calcoliamo la media aritmetica ponderata:

I valori delle deviazioni dalla media e i loro quadrati sono presentati nella tabella. Definiamo la varianza:

La deviazione standard sarà pari a:

Se i dati di origine sono presentati sotto forma di intervallo serie di distribuzione , è necessario prima determinare il valore discreto dell'attributo e quindi applicare il metodo descritto.

Esempio 2.2

Mostriamo il calcolo della varianza per una serie di intervalli utilizzando i dati sulla distribuzione della superficie seminata di una fattoria collettiva in base alla resa del grano.

La media aritmetica è:

Calcoliamo la varianza:

6.3. Calcolo della varianza utilizzando una formula basata su dati individuali

Tecnica di calcolo varianze complesso e con grandi valori di opzioni e frequenze può essere macchinoso. I calcoli possono essere semplificati utilizzando le proprietà di dispersione.

La dispersione ha le seguenti proprietà.

1. Ridurre o aumentare i pesi (frequenze) di una caratteristica variabile di un certo numero di volte non modifica la dispersione.

2. Diminuire o aumentare ciascun valore di una caratteristica della stessa quantità costante UN non cambia la dispersione.

3. Diminuire o aumentare ciascun valore di una caratteristica di un certo numero di volte K rispettivamente riduce o aumenta la varianza in K 2 volte deviazione standard  dentro K una volta.

4. La dispersione di una caratteristica rispetto a un valore arbitrario è sempre maggiore della dispersione rispetto alla media aritmetica per quadrato della differenza tra il valore medio e quello arbitrario:

Se UN 0, allora si arriva alla seguente uguaglianza:

cioè la varianza della caratteristica è pari alla differenza tra il quadrato medio dei valori caratteristici e il quadrato della media.

Ciascuna proprietà può essere utilizzata indipendentemente o in combinazione con altre durante il calcolo della varianza.

La procedura per calcolare la varianza è semplice:

1) determinare significato aritmetico :

2) elevare al quadrato la media aritmetica:

3) eleva al quadrato la deviazione di ciascuna variante della serie:

X io 2 .

4) trova la somma dei quadrati delle opzioni:

5) dividere la somma dei quadrati delle opzioni per il loro numero, cioè determinare il quadrato medio:

6) determinare la differenza tra il quadrato medio della caratteristica e il quadrato della media:

Esempio 3.1 Sono disponibili i seguenti dati sulla produttività dei lavoratori:

Facciamo i seguenti calcoli: