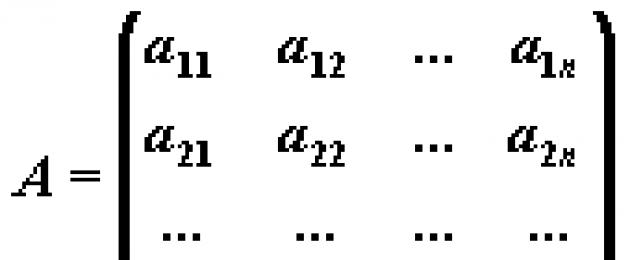Consideriamo sistema di equazioni algebriche lineari(SLAU) relativamente N sconosciuto X 1 , X 2 , ..., X N :
Questo sistema in forma “compressa” può essere scritto come segue:
S N io=1 UN ij X J = b io , i=1,2, ..., n.
In conformità con la regola della moltiplicazione delle matrici, è possibile scrivere il sistema di equazioni lineari considerato forma matriciale Ascia=b, Dove
 ,
,.
,
,.
Matrice UN, le cui colonne sono i coefficienti delle incognite corrispondenti e le righe sono i coefficienti delle incognite nella corrispondente equazione si chiama matrice del sistema. Matrice di colonne B, i cui elementi sono i membri destri delle equazioni del sistema, è chiamata matrice dei membri destri o semplicemente lato destro del sistema. Matrice di colonne X , i cui elementi sono le incognite sconosciute, si chiama soluzione di sistema.
Un sistema di equazioni algebriche lineari scritte nella forma Ascia=b, È equazione di matrice.
Se la matrice del sistema non degenerato, allora ha una matrice inversa e quindi la soluzione del sistema è Ascia=bè dato dalla formula:
x=A -1 B.
Esempio Risolvi il sistema  metodo della matrice.
metodo della matrice.
Soluzione troviamo la matrice inversa per la matrice dei coefficienti del sistema

Calcoliamo il determinante espandendo lungo la prima riga:

Perché il Δ ≠ 0 , Quello UN -1 esiste.

La matrice inversa è stata trovata correttamente.
Troviamo una soluzione al sistema 
Quindi, X 1 = 1,x 2 = 2,x 3 = 3 .
Visita medica: 
7. Il teorema di Kronecker-Capelli sulla compatibilità di un sistema di equazioni algebriche lineari.
Sistema di equazioni lineari ha la forma:
a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2, (5.1)
a m1 x 1 + a m1 x 2 +... + a mn x n = b m.
Qui sono dati a i j e b i (i = ; j = ), e x j sono numeri reali sconosciuti. Utilizzando il concetto di prodotto di matrici, possiamo riscrivere il sistema (5.1) nella forma:
dove A = (a i j) è una matrice costituita da coefficienti per le incognite del sistema (5.1), che prende il nome matrice del sistema, X = (x 1 , x 2 ,..., x n) T , B = (b 1 , b 2 ,..., b m) T sono vettori colonna composti rispettivamente da incognite x j e termini liberi b i .
Raccolta ordinata N si chiamano numeri reali (c 1, c 2,..., c n). soluzione di sistema(5.1), se in seguito alla sostituzione di questi numeri al posto delle corrispondenti variabili x 1, x 2,..., x n, ciascuna equazione del sistema si trasforma in un'identità aritmetica; in altre parole, se esiste un vettore C= (c 1 , c 2 ,..., c n) T tale che AC B.
Viene chiamato il sistema (5.1). giunto, O risolvibile, se ha almeno una soluzione. Il sistema si chiama incompatibile, O irrisolvibile, se non ha soluzioni.
 ,
,
formato assegnando una colonna di termini liberi al lato destro della matrice si chiama A matrice estesa del sistema.
La questione della compatibilità del sistema (5.1) è risolta dal seguente teorema.
Teorema di Kronecker-Capelli . Un sistema di equazioni lineari è coerente se e solo se i ranghi delle matrici A eA coincidono, cioè r(A) = r(A) = r.
Per l’insieme M delle soluzioni del sistema (5.1) esistono tre possibilità:
1) M = (in questo caso il sistema è incoerente);
2) M è costituito da un elemento, cioè il sistema ha un'unica soluzione (in questo caso il sistema si chiama certo);
3) M è costituito da più di un elemento (allora il sistema si chiama incerto). Nel terzo caso il sistema (5.1) ha infinite soluzioni.
Il sistema ha unica soluzione solo se r(A) = n. In questo caso il numero di equazioni non è inferiore al numero di incognite (mn); se m>n, allora le m-n equazioni sono conseguenze delle altre. Se 0 Per risolvere un sistema arbitrario di equazioni lineari, è necessario essere in grado di risolvere sistemi in cui il numero di equazioni è uguale al numero di incognite, le cosiddette Sistemi di tipo Cramer: a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1, a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2, (5.3) ...
... ... ...
... ... a n1 x 1 + a n1 x 2 +... + a nn x n = b n . I sistemi (5.3) vengono risolti in uno dei seguenti modi: 1) il metodo di Gauss, o il metodo di eliminazione delle incognite; 2) secondo le formule di Cramer; 3) metodo matriciale. Esempio 2.12. Esplora il sistema di equazioni e risolvilo se è coerente: 5x 1 - x 2 + 2x 3 + x 4 = 7, 2x 1 + x 2 + 4x 3 - 2x 4 = 1, x 1 - 3x 2 - 6x 3 + 5x 4 = 0. Soluzione. Scriviamo la matrice estesa del sistema:
Calcoliamo il rango della matrice principale del sistema. È ovvio che, ad esempio, il secondo ordine minore in alto a sinistra = 7 0; i minori di terz'ordine che lo contengono sono pari a zero: Di conseguenza, il rango della matrice principale del sistema è 2, cioè r(A) = 2. Per calcolare il rango della matrice estesa A, considerare la matrice minore confinante questo significa che il rango della matrice estesa r(A) = 3. Poiché r(A) r(A), il sistema è incoerente. Questo calcolatore online risolve un sistema di equazioni lineari utilizzando il metodo della matrice. Viene fornita una soluzione molto dettagliata. Per risolvere un sistema di equazioni lineari, seleziona il numero di variabili. Scegli un metodo per calcolare la matrice inversa. Quindi inserisci i dati nelle celle e fai clic sul pulsante "Calcola". ×
Cancellare tutte le celle? Chiudi Cancella Istruzioni per l'inserimento dei dati. I numeri vengono inseriti come numeri interi (esempi: 487, 5, -7623, ecc.), decimali (es. 67., 102,54, ecc.) o frazioni. La frazione deve essere inserita nella forma a/b, dove aeb sono numeri interi o decimali. Esempi 45/5, 6.6/76.4, -7/6.7, ecc. Consideriamo il seguente sistema di equazioni lineari: Data la definizione di matrice inversa, abbiamo UN −1 UN=E, Dove E- matrice identità. Pertanto la (4) può essere scritta come segue: Pertanto, per risolvere il sistema di equazioni lineari (1) (o (2)), è sufficiente moltiplicare l'inverso di UN matrice per vettore di vincolo B. Esempio 1. Risolvi il seguente sistema di equazioni lineari utilizzando il metodo della matrice: Troviamo l'inverso della matrice A utilizzando il metodo Jordan-Gauss. Sul lato destro della matrice UN Scriviamo la matrice identità: Escludiamo gli elementi della prima colonna della matrice sotto la diagonale principale. Per fare ciò, aggiungi le righe 2,3 con la riga 1, moltiplicate rispettivamente per -1/3, -1/3: Escludiamo gli elementi della 2a colonna della matrice sotto la diagonale principale. Per fare ciò, aggiungi la riga 3 con la riga 2 moltiplicata per -24/51: Escludiamo gli elementi della 2a colonna della matrice sopra la diagonale principale. Per fare ciò, aggiungi la riga 1 con la riga 2 moltiplicata per -3/17: Separa il lato destro della matrice. La matrice risultante è la matrice inversa di UN : Forma matriciale per scrivere un sistema di equazioni lineari: Ascia=b, Dove Calcoliamo tutti i complementi algebrici della matrice UN: La matrice inversa si calcola dalla seguente espressione. Un sistema di m equazioni lineari con n incognite chiamato sistema della forma Dove un ij E b i (io=1,…,M; B=1,…,N) sono alcuni numeri noti, e x1,...,xn- sconosciuto. Nella designazione dei coefficienti un ij primo indice io denota il numero dell'equazione e il secondo J– il numero dell'incognita a cui si trova questo coefficiente. Scriveremo i coefficienti per le incognite sotto forma di matrice I numeri sul lato destro delle equazioni sono b 1 ,…,b m sono chiamati membri liberi. Totalità N numeri c 1 ,…,c n chiamato decisione di un dato sistema, se ciascuna equazione del sistema diventa un'uguaglianza dopo aver sostituito dei numeri al suo interno c 1 ,…,c n invece delle corrispondenti incognite x1,...,xn. Il nostro compito sarà trovare soluzioni al sistema. In questo caso si possono verificare tre situazioni: Si dice che un sistema di equazioni lineari che abbia almeno una soluzione giunto. Altrimenti, ad es. se il sistema non ha soluzioni, allora viene chiamato non congiunto. Consideriamo i modi per trovare soluzioni al sistema. METODO MATRICISTICO PER LA RISOLUZIONE DI SISTEMI DI EQUAZIONI LINEARI Le matrici consentono di scrivere brevemente un sistema di equazioni lineari. Sia dato un sistema di 3 equazioni in tre incognite: Consideriamo la matrice del sistema Troviamo il lavoro quelli. come risultato del prodotto, otteniamo i membri sinistri delle equazioni di questo sistema. Quindi, utilizzando la definizione di uguaglianza di matrici, questo sistema può essere scritto nella forma Ecco le matrici UN E B sono noti e la matrice X sconosciuto. È necessario trovarlo, perché... i suoi elementi sono la soluzione a questo sistema. Questa equazione si chiama equazione di matrice. Sia il determinante della matrice diverso da zero | UN| ≠ 0. Quindi l'equazione della matrice viene risolta come segue. Moltiplica entrambi i lati dell'equazione a sinistra per la matrice A-1, inverso della matrice UN: . Perché il LA -1 LA = E E E∙X = X, quindi otteniamo una soluzione all'equazione della matrice nella forma X = A-1B
. Si noti che poiché la matrice inversa può essere trovata solo per matrici quadrate, il metodo della matrice può risolvere solo quei sistemi in cui il numero di equazioni coincide con il numero di incognite. Tuttavia, la registrazione matriciale del sistema è possibile anche nel caso in cui il numero di equazioni non sia uguale al numero di incognite, quindi la matrice UN non sarà quadrato e quindi è impossibile trovare una soluzione al sistema nella forma X = A-1B. Esempi. Risolvere sistemi di equazioni. REGOLA DI CRAMER Consideriamo un sistema di 3 equazioni lineari con tre incognite: Determinante del terzo ordine corrispondente alla matrice del sistema, cioè composto da coefficienti per incognite, chiamato determinante del sistema. Componiamo altri tre determinanti come segue: sostituiamo in sequenza 1, 2 e 3 colonne nel determinante D con una colonna di termini liberi Allora possiamo dimostrare il seguente risultato. Teorema (regola di Cramer). Se il determinante del sistema Δ ≠ 0, allora il sistema in esame ha una ed una sola soluzione, e Prova. Consideriamo quindi un sistema di 3 equazioni in tre incognite. Moltiplichiamo la prima equazione del sistema per il complemento algebrico UN 11 elemento un 11, 2a equazione – on A 21 e 3° – in poi A 31: Aggiungiamo queste equazioni: Diamo un'occhiata a ciascuna delle parentesi e al lato destro di questa equazione. Dal teorema sull'espansione del determinante negli elementi della 1a colonna Allo stesso modo, si può dimostrare che e . Infine, è facile notarlo Otteniamo così l'uguaglianza: . Quindi, . Le uguaglianze e si derivano in modo simile, da cui segue l'enunciato del teorema. Notiamo quindi che se il determinante del sistema Δ ≠ 0, allora il sistema ha un'unica soluzione e viceversa. Se il determinante del sistema è uguale a zero, allora il sistema o ha un numero infinito di soluzioni oppure non ha soluzioni, cioè incompatibile. Esempi. Risolvere il sistema di equazioni METODO GAUSS I metodi precedentemente discussi possono essere utilizzati per risolvere solo quei sistemi in cui il numero di equazioni coincide con il numero di incognite e il determinante del sistema deve essere diverso da zero. Il metodo di Gauss è più universale e adatto a sistemi con qualsiasi numero di equazioni. Consiste nell'eliminazione coerente delle incognite dalle equazioni del sistema. Consideriamo ancora un sistema di tre equazioni in tre incognite: Lasceremo invariata la prima equazione e dalla 2a e 3a escluderemo i termini contenenti x1. Per fare ciò, dividi la seconda equazione per UN 21 e moltiplicare per – UN 11, quindi aggiungilo alla prima equazione. Allo stesso modo, dividiamo la terza equazione per UN 31 e moltiplicare per – UN 11, e poi aggiungerlo al primo. Di conseguenza, il sistema originale assumerà la forma: Ora dall'ultima equazione eliminiamo il termine contenente x2. Per fare ciò, dividi la terza equazione per, moltiplica per e aggiungi per la seconda. Quindi avremo un sistema di equazioni: Da qui, dall'ultima equazione è facile da trovare x3, quindi dalla 2a equazione x2 e infine, dal 1° - x1. Quando si utilizza il metodo gaussiano, le equazioni possono essere scambiate, se necessario. Spesso, invece di scrivere un nuovo sistema di equazioni, si limitano a scrivere la matrice estesa del sistema: e poi portarlo alla forma triangolare o diagonale mediante trasformazioni elementari. A trasformazioni elementari le matrici includono le seguenti trasformazioni: Esempi: Risolvere sistemi di equazioni utilizzando il metodo di Gauss. Il sistema ha quindi un numero infinito di soluzioni. Nella prima parte abbiamo esaminato materiale teorico, il metodo di sostituzione e il metodo di addizione termine per termine delle equazioni del sistema. Consiglio a tutti coloro che accedono al sito tramite questa pagina di leggere la prima parte. Forse alcuni visitatori troveranno il materiale troppo semplice, ma nel processo di risoluzione dei sistemi di equazioni lineari ho fatto una serie di commenti e conclusioni molto importanti riguardanti la soluzione dei problemi matematici in generale. Ora analizzeremo la regola di Cramer e risolveremo un sistema di equazioni lineari utilizzando una matrice inversa (metodo della matrice). Tutti i materiali sono presentati in modo semplice, dettagliato e chiaro; quasi tutti i lettori saranno in grado di imparare come risolvere i sistemi utilizzando i metodi sopra indicati. Per prima cosa esamineremo più da vicino la regola di Cramer per un sistema di due equazioni lineari in due incognite. Per quello? – Dopotutto, il sistema più semplice può essere risolto utilizzando il metodo scolastico, il metodo dell’addizione termine per trimestre! Il fatto è che, anche se a volte, si verifica un compito del genere: risolvere un sistema di due equazioni lineari con due incognite utilizzando le formule di Cramer. In secondo luogo, un esempio più semplice ti aiuterà a capire come utilizzare la regola di Cramer per un caso più complesso: un sistema di tre equazioni con tre incognite. Inoltre, esistono sistemi di equazioni lineari a due variabili, che è consigliabile risolvere utilizzando la regola di Cramer! Consideriamo il sistema di equazioni Nel primo passaggio calcoliamo il determinante, si chiama determinante principale del sistema. Metodo di Gauss. Se , allora il sistema ha un'unica soluzione, e per trovare le radici dobbiamo calcolare altri due determinanti: In pratica, le qualificazioni di cui sopra possono anche essere denotate da una lettera latina. Troviamo le radici dell'equazione usando le formule: Esempio 7 Risolvere un sistema di equazioni lineari Soluzione: Vediamo che i coefficienti dell'equazione sono piuttosto grandi; sul lato destro ci sono le frazioni decimali con una virgola. La virgola è un ospite piuttosto raro nei compiti pratici di matematica; ho preso questo sistema da un problema econometrico. Come risolvere un sistema del genere? Puoi provare a esprimere una variabile in termini di un'altra, ma in questo caso probabilmente ti ritroverai con frazioni terribili e fantasiose con cui è estremamente scomodo lavorare, e il design della soluzione sembrerà semplicemente terribile. Puoi moltiplicare la seconda equazione per 6 e sottrarre termine per termine, ma anche qui si presenteranno le stesse frazioni. Cosa fare? In questi casi, le formule di Cramer vengono in soccorso. ; ; Risposta: , Entrambe le radici hanno code infinite e si trovano approssimativamente, il che è abbastanza accettabile (e perfino banale) per i problemi di econometria. I commenti non sono necessari qui, poiché il compito viene risolto utilizzando formule già pronte, tuttavia, c'è un avvertimento. Quando si utilizza questo metodo, obbligatorio Un frammento della progettazione dell'attività è il seguente frammento: “Ciò significa che il sistema ha una soluzione unica”. Altrimenti, il revisore potrebbe punirti per mancanza di rispetto per il teorema di Cramer. Non sarebbe superfluo il controllo, che può essere comodamente effettuato su una calcolatrice: sostituiamo valori approssimati nella parte sinistra di ciascuna equazione del sistema. Di conseguenza, con un piccolo errore, dovresti ottenere i numeri che si trovano sul lato destro. Esempio 8 Presenta la risposta in frazioni improprie ordinarie. Fai un controllo. Questo è un esempio che puoi risolvere da solo (un esempio del progetto finale e la risposta alla fine della lezione). Passiamo ora a considerare la regola di Cramer per un sistema di tre equazioni in tre incognite: Troviamo il principale determinante del sistema: Se , allora il sistema ha infinite soluzioni oppure è incoerente (non ha soluzioni). In questo caso la regola di Cramer non aiuta; è necessario utilizzare il metodo di Gauss. Se , allora il sistema ha un'unica soluzione e per trovare le radici dobbiamo calcolare altri tre determinanti: E infine, la risposta viene calcolata utilizzando le formule: Come puoi vedere, il caso "tre per tre" non è fondamentalmente diverso dal caso "due per due": la colonna dei termini liberi "cammina" in sequenza da sinistra a destra lungo le colonne del determinante principale. Esempio 9 Risolvi il sistema utilizzando le formule di Cramer. Soluzione: Risolviamo il sistema utilizzando le formule di Cramer. Risposta: In realtà anche qui non c'è niente di speciale da commentare, dato che la soluzione segue formule già pronte. Ma ci sono un paio di commenti. Succede che come risultato dei calcoli si ottengono frazioni irriducibili “cattive”, ad esempio: . 1) Potrebbe esserci un errore nei calcoli. Non appena incontri una frazione “cattiva”, devi immediatamente controllare La condizione è stata riscritta correttamente?. Se la condizione viene riscritta senza errori, è necessario ricalcolare i determinanti utilizzando l'espansione in un'altra riga (colonna). 2) Se non vengono identificati errori a seguito del controllo, molto probabilmente si è verificato un errore di battitura nelle condizioni dell'attività. In questo caso, completa il compito con calma e ATTENZIONE fino alla fine, quindi assicurati di controllare e lo riportiamo sulla carta inviolata dopo la decisione. Naturalmente, controllare una risposta frazionaria è un compito spiacevole, ma sarà un argomento disarmante per l'insegnante, a cui piace davvero dare un segno negativo per qualsiasi stronzata come . Come gestire le frazioni è descritto in dettaglio nella risposta all'Esempio 8. Se hai un computer a portata di mano, utilizza un programma automatizzato per il controllo, che può essere scaricato gratuitamente all'inizio della lezione. A proposito, è più vantaggioso utilizzare subito il programma (anche prima di iniziare la soluzione); vedrai immediatamente il passaggio intermedio in cui hai commesso un errore! Lo stesso calcolatore calcola automaticamente la soluzione del sistema utilizzando il metodo matriciale. Seconda osservazione. Di tanto in tanto ci sono sistemi nelle equazioni in cui mancano alcune variabili, ad esempio: Esempio 10 Risolvi il sistema utilizzando le formule di Cramer. Questo è un esempio di soluzione indipendente (un esempio del progetto finale e la risposta alla fine della lezione). Nel caso di un sistema di 4 equazioni in 4 incognite, le formule di Cramer sono scritte secondo principi simili. Puoi vedere un esempio dal vivo nella lezione Proprietà dei determinanti. Riducendo l'ordine del determinante: cinque determinanti del 4° ordine sono abbastanza risolvibili. Anche se il compito ricorda già molto la scarpa di un professore sul petto di uno studente fortunato. Il metodo della matrice inversa è essenzialmente un caso speciale equazione di matrice(Vedi Esempio n. 3 della lezione specificata). Per studiare questa sezione, devi essere in grado di espandere i determinanti, trovare l'inverso di una matrice ed eseguire la moltiplicazione di matrici. I collegamenti pertinenti verranno forniti man mano che le spiegazioni procedono. Esempio 11 Risolvi il sistema utilizzando il metodo delle matrici Soluzione: Scriviamo il sistema in forma matriciale: Si prega di guardare il sistema di equazioni e matrici. Penso che tutti comprendano il principio con cui scriviamo gli elementi nelle matrici. L'unico commento: se nelle equazioni mancassero alcune variabili, allora gli zeri dovrebbero essere posizionati nei punti corrispondenti della matrice. Troviamo la matrice inversa utilizzando la formula: Per prima cosa, diamo un'occhiata al determinante: Qui il determinante viene espanso sulla prima riga. Attenzione! Se , allora la matrice inversa non esiste ed è impossibile risolvere il sistema utilizzando il metodo delle matrici. In questo caso, il sistema viene risolto con il metodo dell'eliminazione delle incognite (metodo di Gauss). Ora dobbiamo calcolare 9 minori e scriverli nella matrice dei minori Riferimento:È utile conoscere il significato dei doppi pedici in algebra lineare. La prima cifra è il numero della riga in cui si trova l'elemento. La seconda cifra è il numero della colonna in cui si trova l'elemento: Metodo della matrice Soluzioni SLAU applicato alla risoluzione di sistemi di equazioni in cui il numero di equazioni corrisponde al numero di incognite. Il metodo è utilizzato al meglio per risolvere sistemi di ordine basso. Il metodo matriciale per risolvere sistemi di equazioni lineari si basa sull'applicazione delle proprietà della moltiplicazione di matrici. Questo metodo, in altre parole metodo della matrice inversa, così chiamata perché la soluzione si riduce ad un'equazione di matrice ordinaria, per risolvere la quale è necessario trovare la matrice inversa. Metodo di soluzione della matrice Uno SLAE con un determinante maggiore o minore di zero è il seguente: Supponiamo che esista un SLE (sistema di equazioni lineari) con N sconosciuto (su un campo arbitrario): Ciò significa che può essere facilmente convertito in forma matriciale: ASSE=B, Dove UN— la matrice principale del sistema, B E X— colonne dei termini liberi e delle soluzioni del sistema, rispettivamente: Moltiplichiamo questa equazione di matrice da sinistra per A-1— matrice inversa a matrice A: A −1 (AX)=A −1 B. Perché UN −1 LA=E, Significa, X=A −1 B. Il lato destro dell'equazione fornisce la colonna della soluzione del sistema iniziale. La condizione per l'applicabilità del metodo della matrice è la non degenerazione della matrice UN. Condizione necessaria e sufficiente a tal fine è che il determinante della matrice non sia uguale a zero UN: detA≠0. Per sistema omogeneo di equazioni lineari, cioè. se vettore B=0, vale la regola opposta: il sistema AX=0 esiste una soluzione non banale (cioè non uguale a zero) solo quando detA=0. Questa connessione tra soluzioni di sistemi omogenei e disomogenei di equazioni lineari viene chiamata Alternativa a Fredholm. Pertanto, la soluzione dello SLAE utilizzando il metodo della matrice viene eseguita secondo la formula È noto che per una matrice quadrata UN ordine N SU N esiste una matrice inversa A-1 solo se il suo determinante è diverso da zero. Quindi, il sistema N equazioni algebriche lineari con N Risolviamo le incognite utilizzando il metodo della matrice solo se il determinante della matrice principale del sistema non è uguale a zero. Nonostante esistano limitazioni sull'applicabilità di tale metodo e le difficoltà di calcolo per grandi valori di coefficienti e sistemi di ordine elevato, il metodo può essere facilmente implementato su un computer. Innanzitutto, controlliamo se il determinante della matrice dei coefficienti degli SLAE sconosciuti non è uguale a zero. Ora troviamo matrice sindacale, trasponilo e sostituiscilo nella formula per determinare la matrice inversa. Sostituisci le variabili nella formula: Ora troviamo le incognite moltiplicando la matrice inversa e la colonna dei termini liberi. COSÌ, x=2; y=1; z=4. Quando si passa dalla forma usuale di SLAE alla forma matriciale, fare attenzione all'ordine delle variabili sconosciute nelle equazioni del sistema. Per esempio: NON PUÒ essere scritto come: È necessario innanzitutto ordinare le variabili incognite in ciascuna equazione del sistema e solo dopo procedere alla notazione matriciale: Inoltre, è necessario prestare attenzione alla designazione delle variabili sconosciute x1, x2,...,xn potrebbero esserci altre lettere. Per esempio: in forma matriciale lo scriviamo così: Il metodo della matrice è migliore per risolvere sistemi di equazioni lineari in cui il numero di equazioni coincide con il numero di variabili incognite e il determinante della matrice principale del sistema non è uguale a zero. Quando ci sono più di 3 equazioni in un sistema, trovare la matrice inversa richiederà un maggiore sforzo computazionale, quindi, in questo caso, è consigliabile utilizzare il metodo gaussiano per la risoluzione. .
.


Avvertimento
Metodo matriciale per la risoluzione di sistemi di equazioni lineari
Esempi di risoluzione di un sistema di equazioni lineari utilizzando il metodo matriciale
 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
 ,
,
![]() ,
,
![]() ,
,
![]() .
.
 , che chiameremo matrice del sistema.
, che chiameremo matrice del sistema.
 e colonne di matrici di termini sconosciuti e liberi
e colonne di matrici di termini sconosciuti e liberi 

 o più breve UN∙X=B.
o più breve UN∙X=B.



![]()



 .
.



E
, ![]()
![]()
![]()


 ,
,  ,
, 
![]()


, il che significa che il sistema ha una soluzione unica.
![]()

![]()

![]()
![]() .
.
Raccomando il seguente algoritmo di “trattamento”. Se non hai un computer a portata di mano, fai questo:
Qui nella prima equazione non c'è alcuna variabile, nella seconda non c'è alcuna variabile. In questi casi, è molto importante annotare correttamente e ATTENTAMENTE il determinante principale:  – Gli zeri vengono posti al posto delle variabili mancanti.
– Gli zeri vengono posti al posto delle variabili mancanti.
A proposito, è razionale aprire i determinanti con zeri in base alla riga (colonna) in cui si trova lo zero, poiché vengono eseguiti notevolmente meno calcoli.
Risolvere il sistema utilizzando una matrice inversa

, Dove 
, dove è la matrice trasposta dei complementi algebrici dei corrispondenti elementi della matrice.


Cioè, un doppio pedice indica che l'elemento è nella prima riga, terza colonna e, ad esempio, l'elemento è in 3 righe, 2 colonne
![]() . Oppure la soluzione allo SLAE si trova utilizzando matrice inversa A-1.
. Oppure la soluzione allo SLAE si trova utilizzando matrice inversa A-1.Un esempio di risoluzione di uno SLAE non omogeneo.