Ministero dell'Istruzione Generale e Professionale
Università statale del turismo di Sochi
e attività di resort
Istituto Pedagogico
Facoltà di Matematica
Dipartimento di Matematica Generale
LAVORO DI LAUREA
Serie di Fourier e loro applicazioni
nella fisica matematica.
Completato da: studente del 5° anno
firma diurna
Specialità 010100
"Matematica"
Kasperova N.S.
Carta dello studente n. 95471
Consulente scientifico: professore associato, Ph.D.
firma tecnica. Scienze
Pozin P.A.
Soči, 2000
1. Introduzione.
2. Il concetto di serie di Fourier.
2.1. Determinazione dei coefficienti della serie di Fourier.
2.2. Integrali di funzioni periodiche.
3. Criteri di convergenza delle serie di Fourier.
3.1. Esempi di sviluppo di funzioni in serie di Fourier.
4. Cenni sullo sviluppo di una funzione periodica in una serie di Fourier
5. Serie di Fourier per funzioni pari e dispari.
6. Serie di Fourier per funzioni con periodo 2 l .
7. Espansione di Fourier di una funzione non periodica.
Introduzione.
Jean Baptiste Joseph Fourier - matematico francese, membro dell'Accademia delle scienze di Parigi (1817).
Le prime opere di Fourier riguardano l'algebra. Già nelle lezioni del 1796 delineò un teorema sul numero delle radici reali di un'equazione algebrica compresa tra confini dati (ed. 1820), a lui intitolato; una soluzione completa sul numero di radici reali di un'equazione algebrica fu ottenuta nel 1829 da J.Sh.F. Tempesta. Nel 1818 Fourier investigò la questione delle condizioni per l'applicabilità del metodo sviluppato da Newton per la soluzione numerica delle equazioni, non conoscendo risultati simili ottenuti nel 1768 dal matematico francese J.R. Murail. Il risultato del lavoro di Fourier sui metodi numerici per la risoluzione delle equazioni è l'Analisi di alcune equazioni, pubblicata postuma nel 1831.
La principale area di studio di Fourier era la fisica matematica. Nel 1807 e nel 1811 presentò le sue prime scoperte sulla teoria della propagazione del calore nei solidi all'Accademia delle Scienze di Parigi, e nel 1822 pubblicò la famosa opera Teoria analitica del calore, che giocò un ruolo importante nella storia successiva. della matematica. Questa è la teoria matematica della conduzione del calore. A causa della generalità del metodo, questo libro è diventato la fonte di tutti i moderni metodi di fisica matematica. In questo lavoro, Fourier derivò un'equazione differenziale per la conduzione del calore e sviluppò le idee delineate in precedenza da D. Bernoulli nei termini più generali, sviluppò un metodo di separazione delle variabili (metodo di Fourier) per risolvere l'equazione del calore per determinate condizioni al contorno, che si applicò a una serie di casi particolari (cubo, cilindro, ecc.). Questo metodo si basa sulla rappresentazione delle funzioni mediante serie trigonometriche di Fourier.
Le serie di Fourier sono ora diventate uno strumento ben sviluppato nella teoria delle equazioni alle derivate parziali per risolvere problemi ai limiti.
1. Il concetto di serie di Fourier.(pag. 94, Uvarenkov)
Le serie di Fourier svolgono un ruolo importante nella fisica matematica, nella teoria dell'elasticità, nell'ingegneria elettrica e in particolare nel loro caso speciale: le serie trigonometriche di Fourier.
Una serie trigonometrica è una serie della forma
o, simbolicamente:
 (1)
(1)
dove ω, a 0 , a 1 , …, a n , …, b 0 , b 1 , …, b n , … sono numeri costanti (ω>0) .
Alcuni problemi di fisica hanno portato storicamente allo studio di tali serie, ad esempio il problema delle vibrazioni delle corde (XVIII secolo), il problema delle regolarità nei fenomeni di conduzione del calore, ecc. Nelle applicazioni, considerazione delle serie trigonometriche , è principalmente legato al problema di rappresentare un dato movimento, descritto dall'equazione y = ƒ(χ), in
sotto forma di somma delle oscillazioni armoniche più semplici, spesso prese in numero infinitamente grande, cioè come somma di una serie della forma (1).Si arriva quindi al problema seguente: scoprire se per una data funzione ƒ(x) su un dato intervallo esiste una serie (1) che converge a questa funzione su questo intervallo. Se ciò è possibile, allora si dice che la funzione ƒ(x) si espande in una serie trigonometrica su questo intervallo.
La serie (1) converge in un punto x 0, a causa della periodicità delle funzioni
(n=1,2,..), convergerà anche in tutti i punti della forma (m è un intero qualsiasi), e quindi la sua somma S(x) sarà (nella regione di convergenza della serie) un periodico funzione: se S n ( x) è l'ennesima somma parziale di questa serie, allora abbiamo
e quindi
2. Determinazione dei coefficienti della serie mediante le formule di Fourier.
Sia una funzione periodica ƒ(x) con periodo 2π tale da essere rappresentata da una serie trigonometrica convergente a una data funzione nell'intervallo (-π, π), ovvero sia la somma di questa serie:
 . (2)
. (2)
Supponiamo che l'integrale della funzione a sinistra di questa uguaglianza sia uguale alla somma degli integrali dei termini di questa serie. Ciò sarà vero se assumiamo che la serie di numeri composta dai coefficienti della serie trigonometrica data converge assolutamente, cioè la serie di numeri positivi converge
(3)La serie (1) è maggiorata e può essere integrata termine per termine nell'intervallo (-π, π). Integriamo entrambe le parti dell'uguaglianza (2):
.Calcoliamo separatamente ogni integrale che si verifica a destra:
 ,
,
 ,
.
,
.
Così,
 , Dove
, Dove  . (4)
. (4)
Stima dei coefficienti di Fourier.(Bugrov)
Teorema 1. Sia una funzione ƒ(x) di periodo 2π abbia derivata continua ƒ ( s) (x) ordine s che soddisfa la disuguaglianza sull'intero asse reale:
│ ƒ (s) (x)│≤ M s ; (5)
quindi i coefficienti di Fourier della funzione ƒ soddisfare la disuguaglianza
(6)Prova. Integrando per parti e tenendo conto di ciò
ƒ(-π) = ƒ(π), abbiamo


Integrando sequenzialmente il membro destro della (7), tenendo conto che le derivate ƒ ΄ , …, ƒ (s-1) sono continue e assumono gli stessi valori anche nei punti t = -π e t = π come stima (5), si ottiene la prima stima (6).
La seconda stima (6) si ottiene in modo simile.
Teorema 2. I coefficienti di Fourier ƒ(x) soddisfano la disuguaglianza
 (8)
(8)
Prova. Abbiamo
Che sono già piuttosto stufi. E sento che è giunto il momento di estrarre nuovo cibo in scatola dalle riserve strategiche della teoria. È possibile espandere la funzione in una serie in qualche altro modo? Ad esempio, per esprimere un segmento di linea retta in termini di seno e coseno? Sembra incredibile, ma funzioni così apparentemente distanti si prestano a essere soddisfatte
"riunione". Oltre ai gradi familiari di teoria e pratica, esistono altri approcci per espandere una funzione in una serie.
In questa lezione conosceremo la serie trigonometrica di Fourier, toccheremo il problema della sua convergenza e somma e, ovviamente, analizzeremo numerosi esempi di espansione delle funzioni in una serie di Fourier. Volevo sinceramente chiamare l'articolo "Serie Fourier for Dummies", ma sarebbe astuto, poiché la risoluzione dei problemi richiederà la conoscenza di altre sezioni dell'analisi matematica e una certa esperienza pratica. Pertanto, il preambolo assomiglierà all'addestramento degli astronauti =)
Innanzitutto, lo studio dei materiali della pagina dovrebbe essere affrontato in ottima forma. Assonnato, riposato e sobrio. Senza forti emozioni per la zampa rotta di un criceto e pensieri ossessivi sulle difficoltà della vita dei pesci d'acquario. La serie di Fourier non è difficile dal punto di vista della comprensione, tuttavia, i compiti pratici richiedono semplicemente una maggiore concentrazione di attenzione - idealmente, si dovrebbero abbandonare completamente gli stimoli esterni. La situazione è aggravata dal fatto che non esiste un modo semplice per verificare la soluzione e la risposta. Pertanto, se la tua salute è inferiore alla media, è meglio fare qualcosa di più semplice. È vero.
In secondo luogo, prima di volare nello spazio, è necessario studiare il cruscotto della navicella spaziale. Partiamo dai valori delle funzioni che vanno cliccate sulla macchina:
Per qualsiasi valore naturale:
1). E infatti, la sinusoide "fa lampeggiare" l'asse x attraverso ciascun "pi":
. Nel caso di valori negativi dell'argomento il risultato, ovviamente, sarà lo stesso: .
2). Ma non tutti lo sapevano. Il coseno "pi en" è l'equivalente di una "luce lampeggiante":
Un argomento negativo non cambia il caso: ![]() .
.
Forse abbastanza.
E in terzo luogo, caro corpo di cosmonauti, devi essere in grado di ... integrare.
In particolare, certo portare una funzione sotto un segno differenziale, integrare per parti ed essere in buoni rapporti con Formula di Newton-Leibniz. Cominciamo gli importanti esercizi pre-volo. Sconsiglio vivamente di saltarlo, per non appiattirsi in seguito a gravità zero:
Esempio 1
Calcolare integrali definiti

dove assume valori naturali.
Soluzione: si effettua l'integrazione sulla variabile "x" e in questa fase la variabile discreta "en" è considerata una costante. In tutti gli integrali portare la funzione sotto il segno del differenziale:
Una versione breve della soluzione, a cui sarebbe utile sparare, assomiglia a questa:
Abituarsi:
I quattro punti rimanenti sono da soli. Cerca di trattare il compito coscienziosamente e di organizzare gli integrali in modo breve. Soluzioni di esempio alla fine della lezione.
Dopo un esercizio di QUALITÀ, indossiamo le tute spaziali
e prepararsi per iniziare!
Sviluppo di una funzione in una serie di Fourier sull'intervallo
Consideriamo una funzione che determinato almeno sull'intervallo (e, possibilmente, su un intervallo più ampio). Se questa funzione è integrabile sul segmento , allora può essere espansa in una funzione trigonometrica serie di Fourier:![]() , dove sono i cosiddetti Coefficienti di Fourier.
, dove sono i cosiddetti Coefficienti di Fourier.
In questo caso, il numero viene chiamato periodo di decomposizione e il numero è decomposizione dell'emivita.
Ovviamente, nel caso generale, la serie di Fourier è composta da seni e coseni: ![]()
Anzi, scriviamolo nel dettaglio:
Il termine zero della serie viene solitamente scritto come .
I coefficienti di Fourier vengono calcolati utilizzando le seguenti formule: 
Capisco perfettamente che i nuovi termini sono ancora oscuri per i principianti che studiano l'argomento: periodo di decomposizione, mezzo ciclo, Coefficienti di Fourier e altri. Niente panico, non è paragonabile all'eccitazione prima di una passeggiata nello spazio. Scopriamo tutto nell'esempio più vicino, prima di eseguirlo è logico porre domande pratiche urgenti:
Cosa devi fare nelle seguenti attività?
Espandi la funzione in una serie di Fourier. Inoltre, spesso è necessario disegnare il grafico di una funzione, il grafico della somma di una serie, una somma parziale e, nel caso di sofisticate fantasie professorali, fare qualcos'altro.
Come espandere una funzione in una serie di Fourier?
In sostanza, devi trovare Coefficienti di Fourier, cioè componi e calcola tre integrali definiti.
Per favore copia la forma generale della serie di Fourier e le tre formule di lavoro sul tuo quaderno. Sono molto felice che alcuni visitatori del sito abbiano il sogno d'infanzia di diventare un astronauta che si realizza proprio davanti ai miei occhi =)
Esempio 2
Espandi la funzione in una serie di Fourier sull'intervallo . Costruisci un grafico, un grafico della somma di una serie e di una somma parziale.
Soluzione: la prima parte del compito è espandere la funzione in una serie di Fourier.
L'inizio è standard, assicurati di scrivere che:
In questo problema, il periodo di espansione, semiperiodo.
Espandiamo la funzione in una serie di Fourier sull'intervallo: ![]()
Utilizzando le formule appropriate, troviamo Coefficienti di Fourier. Ora dobbiamo comporne e calcolarne tre integrali definiti. Per comodità numerò i punti:
1) Il primo integrale è il più semplice, però richiede già occhio e occhio: 
2) Utilizziamo la seconda formula:
Questo integrale è ben noto e lo prende frammentariamente: 
Quando trovato usato Metodo per portare una funzione sotto un segno differenziale.
Nell'attività in esame, è più conveniente utilizzarlo immediatamente formula per l'integrazione per parti di un integrale definito  :
:

Un paio di note tecniche. Innanzitutto, dopo aver applicato la formula l'intera espressione deve essere racchiusa tra parentesi grandi, poiché c'è una costante davanti all'integrale originale. Non perdiamolo! Le parentesi possono essere aperte in qualsiasi passaggio successivo, l'ho fatto all'ultimo turno. Nel primo "pezzo" ![]() mostriamo un'estrema precisione nella sostituzione, come puoi vedere, la costante è fuori mercato e i limiti di integrazione vengono sostituiti nel prodotto. Questa azione è contrassegnata da parentesi quadre. Ebbene, l'integrale del secondo "pezzo" della formula ti è ben noto dal compito di allenamento ;-)
mostriamo un'estrema precisione nella sostituzione, come puoi vedere, la costante è fuori mercato e i limiti di integrazione vengono sostituiti nel prodotto. Questa azione è contrassegnata da parentesi quadre. Ebbene, l'integrale del secondo "pezzo" della formula ti è ben noto dal compito di allenamento ;-)
E, soprattutto, la massima concentrazione dell'attenzione!
3) Cerchiamo il terzo coefficiente di Fourier:
Si ottiene un parente dell'integrale precedente, che è anche integrato per parti:
Questo caso è un po' più complicato, commenterò i passaggi successivi passo dopo passo: 
(1) L'intera espressione è racchiusa tra parentesi grandi.. Non volevo sembrare noioso, perdono la costante troppo spesso.
(2) In questo caso ho immediatamente espanso quelle parentesi grandi. Attenzione speciale lo dedichiamo al primo “pezzo”: la costante fuma in disparte e non partecipa alla sostituzione dei limiti di integrazione (e) nel prodotto. Considerata la confusione del verbale, è ancora una volta consigliabile evidenziare questa azione tra parentesi quadre. Con il secondo "pezzo" ![]() tutto è più semplice: qui la frazione è apparsa dopo aver aperto le parentesi grandi e la costante - come risultato dell'integrazione del familiare integrale ;-)
tutto è più semplice: qui la frazione è apparsa dopo aver aperto le parentesi grandi e la costante - come risultato dell'integrazione del familiare integrale ;-)
(3) Tra parentesi quadre effettuiamo trasformazioni e nell'integrale destro sostituiamo i limiti di integrazione.
(4) Togliamo il “lampeggiatore” dalle parentesi quadre: , dopodiché apriamo le parentesi interne: .
(5) Cancelliamo 1 e -1 tra parentesi, facciamo le ultime semplificazioni.
Finalmente trovati tutti e tre i coefficienti di Fourier: ![]()
Sostituirli nella formula ![]() :
:
Non dimenticare di dividerlo a metà. Nell'ultimo passaggio si toglie dalla somma la costante ("meno due"), che non dipende da "en".
Abbiamo così ottenuto lo sviluppo della funzione in serie di Fourier sull'intervallo : ![]()
Studiamo la questione della convergenza della serie di Fourier. Spiegherò in particolare la teoria Teorema di Dirichlet, letteralmente "sulle dita", quindi se avete bisogno di formulazioni rigorose, fate riferimento a un libro di testo di calcolo infinitesimale (ad esempio, il 2° volume di Bohan; o il 3° volume di Fichtenholtz, ma in esso è più difficile).
Nella seconda parte dell'attività è necessario disegnare un grafico, un grafico a somma di serie e un grafico a somma parziale.
Il grafico della funzione è il solito retta sul piano, che viene disegnato con una linea tratteggiata nera: 
Ci occupiamo della somma delle serie. Come sai, le serie funzionali convergono in funzioni. Nel nostro caso, la serie di Fourier costruita ![]() per qualsiasi valore di "x" converge alla funzione mostrata in rosso. Questa funzione è soggetta a interruzioni del 1° tipo in punti, ma anche definiti in essi (punti rossi nel disegno)
per qualsiasi valore di "x" converge alla funzione mostrata in rosso. Questa funzione è soggetta a interruzioni del 1° tipo in punti, ma anche definiti in essi (punti rossi nel disegno)
Così: ![]() . È facile vedere che differisce notevolmente dalla funzione originale, motivo per cui nella notazione
. È facile vedere che differisce notevolmente dalla funzione originale, motivo per cui nella notazione ![]() viene utilizzata una tilde al posto del segno di uguale.
viene utilizzata una tilde al posto del segno di uguale.
Studiamo un algoritmo mediante il quale conviene costruire la somma di una serie.
Sull'intervallo centrale la serie di Fourier converge alla funzione stessa (il segmento rosso centrale coincide con la linea tratteggiata nera della funzione lineare).
Ora parliamo un po' della natura dell'espansione trigonometrica considerata. serie di Fourier ![]() comprende solo funzioni periodiche (costante, seno e coseno), quindi la somma della serie
comprende solo funzioni periodiche (costante, seno e coseno), quindi la somma della serie ![]() è anche una funzione periodica.
è anche una funzione periodica.
Cosa significa questo nel nostro esempio particolare? E questo significa che la somma della serie ![]() –necessariamente periodico e il segmento rosso dell'intervallo deve essere ripetuto all'infinito a sinistra e a destra.
–necessariamente periodico e il segmento rosso dell'intervallo deve essere ripetuto all'infinito a sinistra e a destra.
Penso che ora il significato della frase "periodo di decomposizione" sia finalmente diventato chiaro. In poche parole, ogni volta che la situazione si ripete ancora e ancora.
In pratica, di solito è sufficiente rappresentare tre periodi di decomposizione, come avviene nel disegno. Bene, e altri "monconi" dei periodi vicini - per chiarire che il grafico continua.
Di particolare interesse sono Punti di discontinuità di 1° specie. In tali punti la serie di Fourier converge a valori isolati, che si trovano esattamente al centro del "salto" di discontinuità (punti rossi nel disegno). Come trovare l'ordinata di questi punti? Per prima cosa troviamo l'ordinata del "piano superiore": per questo calcoliamo il valore della funzione nel punto più a destra del periodo di espansione centrale: . Per calcolare l’ordinata del “piano inferiore”, il modo più semplice è prendere il valore più a sinistra dello stesso periodo: ![]() . L'ordinata del valore medio è la media aritmetica della somma di "superiore e inferiore": . È bello il fatto che quando costruisci un disegno, vedrai immediatamente se il centro è calcolato correttamente o in modo errato.
. L'ordinata del valore medio è la media aritmetica della somma di "superiore e inferiore": . È bello il fatto che quando costruisci un disegno, vedrai immediatamente se il centro è calcolato correttamente o in modo errato.
Costruiamo una somma parziale della serie e ripetiamo allo stesso tempo il significato del termine "convergenza". Il motivo è noto dalla lezione su la somma delle serie di numeri. Descriviamo nel dettaglio la nostra ricchezza:
Per fare una somma parziale, devi scrivere zero + altri due termini della serie. Questo è,
Nel disegno, il grafico della funzione è mostrato in verde e, come puoi vedere, avvolge abbastanza strettamente la somma totale. Se consideriamo la somma parziale di cinque termini della serie, il grafico di questa funzione si avvicinerà alle linee rosse in modo ancora più accurato, se ci sono cento termini, il "serpente verde" si fonderà effettivamente completamente con i segmenti rossi, eccetera. Pertanto la serie di Fourier converge alla sua somma.
È interessante notare che qualsiasi somma parziale lo è funzione continua, ma la somma totale della serie è ancora discontinua.
In pratica, non è raro costruire un grafico a somma parziale. Come farlo? Nel nostro caso è necessario considerare la funzione sul segmento, calcolarne i valori alle estremità del segmento e nei punti intermedi (più punti consideri, più accurato sarà il grafico). Quindi dovresti segnare questi punti sul disegno e disegnare attentamente un grafico sul periodo, quindi “replicarlo” in intervalli adiacenti. In quale altro modo? Dopotutto, anche l'approssimazione è una funzione periodica... ... il suo grafico mi ricorda in qualche modo un ritmo cardiaco uniforme sul display di un dispositivo medico.
Certo, non è molto comodo eseguire la costruzione, poiché bisogna essere estremamente attenti, mantenendo una precisione non inferiore al mezzo millimetro. Tuttavia, soddisferò i lettori che sono in disaccordo con il disegno: in un compito "reale", non è sempre necessario eseguire un disegno, da qualche parte nel 50% dei casi è necessario espandere la funzione in una serie di Fourier e questo è Esso.
Dopo aver completato il disegno, completiamo l'attività:
Risposta: ![]()
In molti compiti, la funzione soffre rottura del 1° tipo proprio sul periodo di decomposizione:
Esempio 3
Sviluppare in serie di Fourier la funzione data sull'intervallo . Disegna un grafico della funzione e della somma totale della serie.
![]()
La funzione proposta è data a tratti (e, attenzione, solo sul segmento) e sopportare rottura del 1° tipo al punto . È possibile calcolare i coefficienti di Fourier? Nessun problema. Sia la parte sinistra che quella destra della funzione sono integrabili sui loro intervalli, quindi gli integrali in ciascuna delle tre formule dovrebbero essere rappresentati come la somma di due integrali. Vediamo, ad esempio, come si fa per un coefficiente zero:
Il secondo integrale si è rivelato uguale a zero, il che ha ridotto il lavoro, ma non è sempre così.
Altri due coefficienti di Fourier sono scritti in modo simile.
Come visualizzare la somma di una serie? Sull'intervallo sinistro disegniamo un segmento di linea retta e sull'intervallo - un segmento di linea retta (evidenzia la sezione dell'asse in grassetto-grassetto). Cioè, nell'intervallo di espansione, la somma della serie coincide con la funzione ovunque, tranne che in tre punti "cattivi". Nel punto di discontinuità della funzione, la serie di Fourier converge ad un valore isolato, che si trova esattamente nel mezzo del “salto” della discontinuità. Non è difficile vederlo oralmente: limite sinistro:, limite destro: ![]() e, ovviamente, l'ordinata del punto medio è 0,5.
e, ovviamente, l'ordinata del punto medio è 0,5.
A causa della periodicità della somma , l'immagine deve essere “moltiplicata” in periodi vicini, in particolare, rappresentare la stessa cosa negli intervalli e . In questo caso, nei punti, la serie di Fourier converge ai valori mediani.
In effetti, qui non c'è nulla di nuovo.
Prova a risolvere questo problema da solo. Un esempio approssimativo di disegno e disegno fine alla fine della lezione.
Sviluppo di una funzione in una serie di Fourier su un periodo arbitrario
Per un periodo di espansione arbitrario, dove "el" è un numero positivo qualsiasi, le formule per la serie di Fourier e i coefficienti di Fourier differiscono in un argomento seno e coseno leggermente più complicato:

Se , otteniamo le formule per l'intervallo con cui abbiamo iniziato.
L'algoritmo e i principi per risolvere il problema sono completamente preservati, ma aumenta la complessità tecnica dei calcoli:
Esempio 4
Espandi la funzione in una serie di Fourier e traccia la somma. ![]()
Soluzione: in effetti, un analogo dell'esempio n. 3 con rottura del 1° tipo al punto . In questo problema, il periodo di espansione, semiperiodo. La funzione è definita solo sul semiintervallo, ma questo non cambia le cose: è importante che entrambe le parti della funzione siano integrabili.
Espandiamo la funzione in una serie di Fourier:
Poiché la funzione è discontinua all’origine, ogni coefficiente di Fourier va ovviamente scritto come somma di due integrali:
1) Scriverò il primo integrale il più dettagliato possibile:
2) Scruta attentamente la superficie della luna:
Secondo integrale prendere in parti:

A cosa dovresti prestare molta attenzione dopo aver aperto la continuazione della soluzione con un asterisco?
Innanzitutto non perdiamo il primo integrale  , dove eseguiamo immediatamente portando sotto il segno del differenziale. In secondo luogo, non dimenticare la sfortunata costante prima delle parentesi grandi e non lasciarti confondere dai segni quando si utilizza la formula
, dove eseguiamo immediatamente portando sotto il segno del differenziale. In secondo luogo, non dimenticare la sfortunata costante prima delle parentesi grandi e non lasciarti confondere dai segni quando si utilizza la formula  . Dopotutto, è più conveniente aprire le parentesi grandi immediatamente nel passaggio successivo.
. Dopotutto, è più conveniente aprire le parentesi grandi immediatamente nel passaggio successivo.
Il resto è una questione di tecnica, solo un'esperienza insufficiente nella risoluzione degli integrali può causare difficoltà.
Sì, non è stato vano che gli eminenti colleghi del matematico francese Fourier fossero indignati: come ha osato scomporre le funzioni in serie trigonometriche ?! =) A proposito, probabilmente tutti sono interessati al significato pratico del compito in questione. Lo stesso Fourier lavorò su un modello matematico della conduzione del calore, e successivamente la serie a lui intitolata iniziò ad essere utilizzata per studiare molti processi periodici, apparentemente invisibili nel mondo esterno. Ora, a proposito, mi sono sorpreso a pensare che non fosse un caso che avessi confrontato il grafico del secondo esempio con un ritmo cardiaco periodico. Chi è interessato può conoscere l'applicazione pratica Trasformate di Fourier da fonti di terze parti. ... Anche se è meglio di no, sarà ricordato come il Primo Amore =)
3) Dati i legami deboli più volte citati, trattiamo il terzo coefficiente:
Integrazione per parti: 

Sostituiamo nella formula i coefficienti di Fourier trovati ![]() , senza dimenticare di dividere a metà il coefficiente zero:
, senza dimenticare di dividere a metà il coefficiente zero:
Tracciamo la somma della serie. Ripetiamo brevemente la procedura: sull'intervallo costruiamo una linea e sull'intervallo - una linea. Con un valore pari a zero "x", mettiamo un punto al centro del "salto" del gap e "replichiamo" il grafico per i periodi vicini: 
Nelle "congiunzioni" dei periodi la somma sarà pari anche ai punti medi del "salto" del divario.
Pronto. Ti ricordo che la funzione stessa è condizionatamente definita solo sul semiintervallo e, ovviamente, coincide con la somma delle serie sugli intervalli
Risposta:
Talvolta una determinata funzione a tratti è continua anche nel periodo di espansione. L'esempio più semplice: ![]() . Soluzione (Vedi Bohan Volume 2)è lo stesso dei due esempi precedenti: nonostante continuità della funzione nel punto , ciascun coefficiente di Fourier è espresso come somma di due integrali.
. Soluzione (Vedi Bohan Volume 2)è lo stesso dei due esempi precedenti: nonostante continuità della funzione nel punto , ciascun coefficiente di Fourier è espresso come somma di due integrali.
Nell'intervallo di rottura Punti di discontinuità di 1° specie e/o punti di "giunzione" del grafico possono essere più (due, tre, ed in generale qualsiasi finale quantità). Se una funzione è integrabile in ogni sua parte, allora è anche espandibile in serie di Fourier. Ma per esperienza pratica, non ricordo una scatola del genere. Tuttavia, ci sono compiti più difficili di quelli appena considerati, e alla fine dell'articolo per tutti ci sono collegamenti a serie di Fourier di maggiore complessità.
Nel frattempo rilassiamoci, appoggiandoci allo schienale delle nostre sedie e contemplando le infinite distese di stelle:
Esempio 5
Espandi la funzione in una serie di Fourier sull'intervallo e traccia la somma delle serie.
In questo compito, la funzione continuo sul semiintervallo di decomposizione, che semplifica la soluzione. Tutto è molto simile all'esempio n. 2. Non puoi allontanarti dall'astronave, devi decidere =) Esempio di progettazione alla fine della lezione, il programma è allegato.
Espansione in serie di Fourier delle funzioni pari e dispari
Con le funzioni pari e dispari, il processo di risoluzione del problema è notevolmente semplificato. Ed ecco perché. Torniamo allo sviluppo della funzione in una serie di Fourier su un periodo di "due pi greco" ![]() e periodo arbitrario "due birre"
e periodo arbitrario "due birre" ![]() .
.
Supponiamo che la nostra funzione sia pari. Il termine generale della serie, come puoi vedere, contiene coseni pari e seni dispari. E se scomponiamo una funzione PARI, allora perché abbiamo bisogno dei seni dispari?! Ripristiniamo il coefficiente non necessario: .
Così, una funzione pari si espande in una serie di Fourier solo in coseni:
Perché il integrali di funzioni pari su un segmento di integrazione simmetrico rispetto allo zero si può raddoppiare, allora si semplificano anche i rimanenti coefficienti di Fourier.
Per intervallo: 
Per un intervallo arbitrario: 
Gli esempi di libri di testo che si trovano in quasi tutti i libri di testo di calcolo includono espansioni di funzioni pari ![]() . Inoltre, si sono incontrati più volte nella mia pratica personale:
. Inoltre, si sono incontrati più volte nella mia pratica personale:
Esempio 6
Data una funzione. Necessario:
1) espandere la funzione in una serie di Fourier con periodo , dove è un numero positivo arbitrario;
2) annotare lo sviluppo sull'intervallo, costruire una funzione e rappresentare graficamente la somma totale della serie.
Soluzione: nel primo paragrafo si propone di risolvere il problema in modo generale, e questo è molto comodo! Ce ne sarà bisogno: sostituisci semplicemente il tuo valore.
1) In questo problema, il periodo di espansione, semiperiodo. Nel corso di ulteriori azioni, in particolare durante l'integrazione, "el" è considerato una costante
La funzione è pari, il che significa che si espande in una serie di Fourier solo in coseni: ![]() .
.
I coefficienti di Fourier sono ricercati dalle formule  . Presta attenzione ai loro vantaggi assoluti. Innanzitutto l'integrazione avviene sul segmento positivo dell'espansione, il che significa che ci liberiamo del modulo in modo sicuro
. Presta attenzione ai loro vantaggi assoluti. Innanzitutto l'integrazione avviene sul segmento positivo dell'espansione, il che significa che ci liberiamo del modulo in modo sicuro ![]() , considerando solo "x" di due pezzi. E, in secondo luogo, l'integrazione è notevolmente semplificata.
, considerando solo "x" di due pezzi. E, in secondo luogo, l'integrazione è notevolmente semplificata.
Due: 
Integrazione per parti:


Così:
, mentre dalla somma viene tolta la costante , che non dipende da "en".
Risposta: 
2) Scriviamo l'espansione sull'intervallo, per questo sostituiamo il valore desiderato del semiperiodo nella formula generale:
Serie di Fourier di funzioni periodiche con periodo 2π.
La serie di Fourier permette di studiare le funzioni periodiche scomponendole in componenti. Correnti e tensioni alternate, spostamenti, velocità e accelerazione dei manovellismi e onde acustiche sono tipici esempi pratici dell'applicazione delle funzioni periodiche nei calcoli ingegneristici.
Lo sviluppo in serie di Fourier si basa sul presupposto che tutte le funzioni di importanza pratica nell'intervallo -π ≤ x ≤ π possano essere espresse come serie trigonometriche convergenti (una serie è considerata convergente se converge la successione delle somme parziali costituite dai suoi membri) :
Notazione standard (=usuale) attraverso la somma di sinx e cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
dove a o , a 1 ,a 2 ,...,b 1 ,b 2 ,.. sono costanti reali, cioè
Dove, per l'intervallo da -π a π, i coefficienti della serie di Fourier sono calcolati dalle formule:

Si chiamano i coefficienti a o ,an e b n Coefficienti di Fourier, e se possono essere trovati, allora viene chiamata la serie (1). vicino a Fourier, corrispondente alla funzione f(x). Per la serie (1), il termine (a 1 cosx+b 1 sinx) è detto primo o armonica principale,
Un altro modo per scrivere una serie è usare la relazione acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Dove a o è una costante, c 1 \u003d (a 1 2 +b 1 2) 1/2, c n \u003d (a n 2 +b n 2) 1/2 sono le ampiezze delle varie componenti, ed è uguale a a n \ u003d arctg a n /b n.
Per la serie (1), il termine (a 1 cosx + b 1 sinx) oppure c 1 sin (x + α 1) è detto primo o armonica principale,(a 2 cos2x+b 2 sin2x) oppure c 2 sin(2x+α 2) si chiama seconda armonica e così via.
Per rappresentare accuratamente un segnale complesso, di solito è necessario un numero infinito di termini. Tuttavia, in molti problemi pratici è sufficiente considerare solo i primi termini.
Serie di Fourier di funzioni non periodiche con periodo 2π.
Scomposizione di funzioni non periodiche.
Se la funzione f(x) non è periodica, non può essere sviluppata in una serie di Fourier per tutti i valori di x. Tuttavia, è possibile definire una serie di Fourier che rappresenta una funzione su qualsiasi intervallo di larghezza 2π.
Data una funzione non periodica, è possibile comporre una nuova funzione scegliendo valori f(x) entro un certo intervallo e ripetendoli al di fuori di questo intervallo a intervalli di 2π. Poiché la nuova funzione è periodica con periodo 2π, può essere sviluppata in serie di Fourier per tutti i valori di x. Ad esempio, la funzione f(x)=x non è periodica. Tuttavia, se è necessario espanderlo in una serie di Fourier sull'intervallo da 0 a 2π, allora viene costruita una funzione periodica con periodo 2π al di fuori di questo intervallo (come mostrato nella figura seguente).

Per funzioni non periodiche come f(x)=x, la somma della serie di Fourier è uguale al valore di f(x) in tutti i punti dell'intervallo dato, ma non è uguale a f(x) per i punti fuori portata. Per trovare la serie di Fourier di una funzione non periodica nell'intervallo 2π si utilizza la stessa formula dei coefficienti di Fourier.
Funzioni pari e dispari.
Dicono che la funzione y=f(x) Anche se f(-x)=f(x) per tutti i valori di x. I grafici delle funzioni pari sono sempre simmetrici rispetto all'asse y (cioè sono specchiati). Due esempi di funzioni pari: y=x 2 e y=cosx.
Dicono che la funzione y=f(x) strano, se f(-x)=-f(x) per tutti i valori di x. I grafici delle funzioni dispari sono sempre simmetrici rispetto all'origine.
Molte funzioni non sono né pari né dispari.
Espansione in serie di Fourier in coseni.
La serie di Fourier di una funzione periodica pari f(x) con periodo 2π contiene solo termini coseno (cioè non contiene termini seno) e può includere un termine costante. Quindi,

dove sono i coefficienti della serie di Fourier,

La serie di Fourier di una funzione periodica dispari f(x) con periodo 2π contiene solo termini con seni (cioè non contiene termini con coseni).
Quindi,

dove sono i coefficienti della serie di Fourier,

Serie di Fourier su un semiciclo.
Se una funzione è definita per un intervallo, ad esempio da 0 a π, e non solo da 0 a 2π, può essere espansa in una serie solo in termini di seno o solo in termini di coseno. La serie di Fourier risultante viene chiamata vicino a Fourier su un mezzo ciclo.
Se vuoi ottenere una scomposizione Fourier su un semiciclo in coseni funzioni f(x) nell'intervallo da 0 a π, allora è necessario comporre una funzione periodica pari. Nella fig. di seguito è riportata la funzione f(x)=x costruita sull'intervallo da x=0 a x=π. Poiché la funzione pari è simmetrica rispetto all'asse f(x), tracciamo la linea AB, come mostrato in Fig. sotto. Se assumiamo che al di fuori dell'intervallo considerato, la forma triangolare risultante sia periodica con periodo 2π, allora il grafico finale avrà la forma display. nella fig. sotto. Poiché è necessario ottenere lo sviluppo di Fourier in coseni, come prima, calcoliamo i coefficienti di Fourier a o e a n


Se hai bisogno di ottenere Espansione di Fourier del semiciclo sinusoidale funzione f(x) nell'intervallo da 0 a π, allora è necessario comporre una funzione periodica dispari. Nella fig. di seguito è riportata la funzione f(x)=x costruita sull'intervallo da x=0 a x=π. Poiché la funzione dispari è simmetrica rispetto all'origine, costruiamo la retta CD, come mostrato in Fig. Se assumiamo che al di fuori dell'intervallo considerato, il segnale a dente di sega ricevuto sia periodico con periodo 2π, allora il grafico finale avrà la forma mostrata in Fig. Poiché è necessario ottenere l'espansione di Fourier su un semiciclo in termini di seno, come prima, calcoliamo il coefficiente di Fourier. B

Serie di Fourier per un intervallo arbitrario.
Sviluppo di una funzione periodica con periodo L.
La funzione periodica f(x) si ripete quando x aumenta di L, cioè f(x+L)=f(x). Il passaggio dalle funzioni con periodo 2π precedentemente considerate alle funzioni con periodo L è abbastanza semplice, poiché può essere effettuato mediante un cambio di variabile.
Per trovare la serie di Fourier della funzione f(x) nell'intervallo -L/2≤x≤L/2, introduciamo una nuova variabile u in modo che la funzione f(x) abbia un periodo di 2π rispetto a u. Se u=2πx/L, allora x=-L/2 per u=-π e x=L/2 per u=π. Sia anche f(x)=f(Lu/2π)=F(u). La serie di Fourier F(u) ha la forma
(I limiti di integrazione possono essere sostituiti da qualsiasi intervallo di lunghezza L, ad esempio da 0 a L)
Serie di Fourier su semiciclo per funzioni date nell'intervallo L≠2π.
Per la sostituzione u=πx/L, l'intervallo da x=0 a x=L corrisponde all'intervallo da u=0 a u=π. Pertanto la funzione può essere sviluppata in una serie solo in termini di coseni o solo in termini di seni, cioè V Serie di Fourier su semiciclo.
L'espansione in coseni nell'intervallo da 0 a L ha la forma
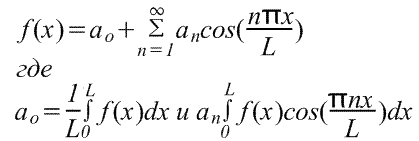
Serie di Fourier di funzioni periodiche con periodo 2π.
La serie di Fourier permette di studiare le funzioni periodiche scomponendole in componenti. Correnti e tensioni alternate, spostamenti, velocità e accelerazione dei manovellismi e onde acustiche sono tipici esempi pratici dell'applicazione delle funzioni periodiche nei calcoli ingegneristici.
Lo sviluppo in serie di Fourier si basa sul presupposto che tutte le funzioni di importanza pratica nell'intervallo -π ≤ x ≤ π possano essere espresse come serie trigonometriche convergenti (una serie è considerata convergente se converge la successione delle somme parziali costituite dai suoi membri) :
Notazione standard (=usuale) attraverso la somma di sinx e cosx
f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,
dove a o , a 1 ,a 2 ,...,b 1 ,b 2 ,.. sono costanti reali, cioè
Dove, per l'intervallo da -π a π, i coefficienti della serie di Fourier sono calcolati dalle formule:

Si chiamano i coefficienti a o ,an e b n Coefficienti di Fourier, e se possono essere trovati, allora viene chiamata la serie (1). vicino a Fourier, corrispondente alla funzione f(x). Per la serie (1), il termine (a 1 cosx+b 1 sinx) è detto primo o armonica principale,
Un altro modo per scrivere una serie è usare la relazione acosx+bsinx=csin(x+α)
f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)
Dove a o è una costante, c 1 \u003d (a 1 2 +b 1 2) 1/2, c n \u003d (a n 2 +b n 2) 1/2 sono le ampiezze delle varie componenti, ed è uguale a a n \ u003d arctg a n /b n.
Per la serie (1), il termine (a 1 cosx + b 1 sinx) oppure c 1 sin (x + α 1) è detto primo o armonica principale,(a 2 cos2x+b 2 sin2x) oppure c 2 sin(2x+α 2) si chiama seconda armonica e così via.
Per rappresentare accuratamente un segnale complesso, di solito è necessario un numero infinito di termini. Tuttavia, in molti problemi pratici è sufficiente considerare solo i primi termini.
Serie di Fourier di funzioni non periodiche con periodo 2π.
Scomposizione di funzioni non periodiche.
Se la funzione f(x) non è periodica, non può essere sviluppata in una serie di Fourier per tutti i valori di x. Tuttavia, è possibile definire una serie di Fourier che rappresenta una funzione su qualsiasi intervallo di larghezza 2π.
Data una funzione non periodica, è possibile comporre una nuova funzione scegliendo valori f(x) entro un certo intervallo e ripetendoli al di fuori di questo intervallo a intervalli di 2π. Poiché la nuova funzione è periodica con periodo 2π, può essere sviluppata in serie di Fourier per tutti i valori di x. Ad esempio, la funzione f(x)=x non è periodica. Tuttavia, se è necessario espanderlo in una serie di Fourier sull'intervallo da 0 a 2π, allora viene costruita una funzione periodica con periodo 2π al di fuori di questo intervallo (come mostrato nella figura seguente).

Per funzioni non periodiche come f(x)=x, la somma della serie di Fourier è uguale al valore di f(x) in tutti i punti dell'intervallo dato, ma non è uguale a f(x) per i punti fuori portata. Per trovare la serie di Fourier di una funzione non periodica nell'intervallo 2π si utilizza la stessa formula dei coefficienti di Fourier.
Funzioni pari e dispari.
Dicono che la funzione y=f(x) Anche se f(-x)=f(x) per tutti i valori di x. I grafici delle funzioni pari sono sempre simmetrici rispetto all'asse y (cioè sono specchiati). Due esempi di funzioni pari: y=x 2 e y=cosx.
Dicono che la funzione y=f(x) strano, se f(-x)=-f(x) per tutti i valori di x. I grafici delle funzioni dispari sono sempre simmetrici rispetto all'origine.
Molte funzioni non sono né pari né dispari.
Espansione in serie di Fourier in coseni.
La serie di Fourier di una funzione periodica pari f(x) con periodo 2π contiene solo termini coseno (cioè non contiene termini seno) e può includere un termine costante. Quindi,

dove sono i coefficienti della serie di Fourier,

La serie di Fourier di una funzione periodica dispari f(x) con periodo 2π contiene solo termini con seni (cioè non contiene termini con coseni).
Quindi,

dove sono i coefficienti della serie di Fourier,

Serie di Fourier su un semiciclo.
Se una funzione è definita per un intervallo, ad esempio da 0 a π, e non solo da 0 a 2π, può essere espansa in una serie solo in termini di seno o solo in termini di coseno. La serie di Fourier risultante viene chiamata vicino a Fourier su un mezzo ciclo.
Se vuoi ottenere una scomposizione Fourier su un semiciclo in coseni funzioni f(x) nell'intervallo da 0 a π, allora è necessario comporre una funzione periodica pari. Nella fig. di seguito è riportata la funzione f(x)=x costruita sull'intervallo da x=0 a x=π. Poiché la funzione pari è simmetrica rispetto all'asse f(x), tracciamo la linea AB, come mostrato in Fig. sotto. Se assumiamo che al di fuori dell'intervallo considerato, la forma triangolare risultante sia periodica con periodo 2π, allora il grafico finale avrà la forma display. nella fig. sotto. Poiché è necessario ottenere lo sviluppo di Fourier in coseni, come prima, calcoliamo i coefficienti di Fourier a o e a n


Se hai bisogno di ottenere Espansione di Fourier del semiciclo sinusoidale funzione f(x) nell'intervallo da 0 a π, allora è necessario comporre una funzione periodica dispari. Nella fig. di seguito è riportata la funzione f(x)=x costruita sull'intervallo da x=0 a x=π. Poiché la funzione dispari è simmetrica rispetto all'origine, costruiamo la retta CD, come mostrato in Fig. Se assumiamo che al di fuori dell'intervallo considerato, il segnale a dente di sega ricevuto sia periodico con periodo 2π, allora il grafico finale avrà la forma mostrata in Fig. Poiché è necessario ottenere l'espansione di Fourier su un semiciclo in termini di seno, come prima, calcoliamo il coefficiente di Fourier. B

Serie di Fourier per un intervallo arbitrario.
Sviluppo di una funzione periodica con periodo L.
La funzione periodica f(x) si ripete quando x aumenta di L, cioè f(x+L)=f(x). Il passaggio dalle funzioni con periodo 2π precedentemente considerate alle funzioni con periodo L è abbastanza semplice, poiché può essere effettuato mediante un cambio di variabile.
Per trovare la serie di Fourier della funzione f(x) nell'intervallo -L/2≤x≤L/2, introduciamo una nuova variabile u in modo che la funzione f(x) abbia un periodo di 2π rispetto a u. Se u=2πx/L, allora x=-L/2 per u=-π e x=L/2 per u=π. Sia anche f(x)=f(Lu/2π)=F(u). La serie di Fourier F(u) ha la forma
(I limiti di integrazione possono essere sostituiti da qualsiasi intervallo di lunghezza L, ad esempio da 0 a L)
Serie di Fourier su semiciclo per funzioni date nell'intervallo L≠2π.
Per la sostituzione u=πx/L, l'intervallo da x=0 a x=L corrisponde all'intervallo da u=0 a u=π. Pertanto la funzione può essere sviluppata in una serie solo in termini di coseni o solo in termini di seni, cioè V Serie di Fourier su semiciclo.
L'espansione in coseni nell'intervallo da 0 a L ha la forma
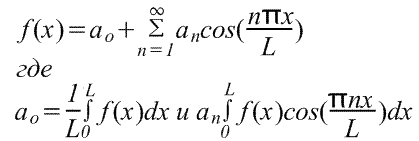
La serie di Fourier di una funzione periodica pari f(x) con periodo 2p contiene solo termini coseno (cioè non contiene termini seno) e può includere un termine costante. Quindi,
dove sono i coefficienti della serie di Fourier,
Espansione di Fourier nei seni
La serie di Fourier di una funzione periodica dispari f (x) con un periodo di 2p contiene solo termini con seni (cioè non contiene termini con coseni).
Quindi,
dove sono i coefficienti della serie di Fourier,
Serie di Fourier su semiciclo
Se una funzione è definita per un intervallo, ad esempio da 0 a p, e non solo da 0 a 2p, può essere espansa in una serie solo in termini di seno o solo in termini di coseno. La serie di Fourier risultante viene chiamata vicino Fourier SU mezzo ciclo.
Se vuoi ottenere una scomposizione Fourier SU mezzo ciclo Di coseni funzioni f (x) nell'intervallo da 0 a p, allora è necessario comporre una funzione periodica pari. Nella fig. di seguito è riportata la funzione f (x) =x, costruita sull'intervallo da x=0 a x=p. Poiché la funzione pari è simmetrica rispetto all'asse f (x), tracciamo la linea AB, come mostrato in Fig. sotto. Se assumiamo che al di fuori dell'intervallo considerato, la forma triangolare risultante sia periodica con periodo 2p, allora il grafico finale avrà la forma display. nella fig. sotto. Poiché è necessario ottenere lo sviluppo di Fourier in coseni, come prima, calcoliamo i coefficienti di Fourier a o e a n


Se hai bisogno di ottenere decomposizione Fourier SU mezzo ciclo Di seni funzioni f (x) nell'intervallo da 0 a p, allora è necessario comporre una funzione periodica dispari. Nella fig. di seguito è riportata la funzione f(x)=x costruita sull'intervallo da x=0 a x=p. Poiché la funzione dispari è simmetrica rispetto all'origine, costruiamo la retta CD, come mostrato in Fig.
Se assumiamo che al di fuori dell'intervallo considerato, il segnale a dente di sega ricevuto sia periodico con periodo 2p, allora il grafico finale avrà la forma mostrata in Fig. Poiché è necessario ottenere l'espansione di Fourier su un semiciclo in termini di seno, come prima, calcoliamo il coefficiente di Fourier. B
- In contatto con 0
- Google+ 0
- OK 0
- Facebook 0