Lati opposti del quadrilatero circoscritto. Formule con diagonali

Da Wikipedia, l'enciclopedia libera

Nella geometria euclidea, quadrilatero inscrittoè un quadrilatero in cui tutti i vertici giacciono sulla stessa circonferenza. Questo cerchio si chiama cerchio circoscritto quadrilatero e si dice che i vertici giacciono sulla stessa circonferenza. Il centro di questo cerchio e il suo raggio si chiamano rispettivamente centro E raggio cerchio circoscritto. Altri termini per questo quadrilatero: quadrilatero giace sulla stessa circonferenza, i lati dell'ultimo quadrilatero sono le corde del cerchio. Di solito si presume che un quadrilatero convesso sia un quadrilatero convesso. Le formule e le proprietà fornite di seguito sono valide nel caso convesso.
Dicono che se un cerchio può essere circoscritto attorno ad un quadrilatero, Quello in questo cerchio è inscritto il quadrilatero, e viceversa.

Criteri generali per l'iscrizione di un quadrilatero

Circa un quadrilatero convesso $\pi$ radiante), ovvero:

\angolo A+\angolo C = \angolo B + \angolo D = 180^\circonferenza

o nella notazione della figura:

$\alpha + \gamma = \beta + \delta = \pi = 180^(\circ).$

È possibile descrivere un cerchio attorno a qualsiasi quadrilatero, in cui quattro bisettrici perpendicolari dei suoi lati (o mediatrici dei suoi lati, cioè perpendicolari ai lati passanti per i loro punti medi) si intersecano in un punto.
È possibile circoscrivere un cerchio attorno a qualsiasi quadrilatero a cui sia adiacente un angolo esterno dato l'angolo interno, esattamente uguale ad un altro angolo interno opposto dato angolo interno. Infatti questa condizione è la condizione di antiparallelismo di due lati opposti del quadrilatero. Nella fig. gli angoli esterni e interni adiacenti del pentagono verde sono mostrati sotto.

\displaystyle AX\cdot XC = BX\cdot XD.

intersezione X può essere interno o esterno al cerchio. Nel primo caso otteniamo il quadrilatero inscritto ABCD, e in quest'ultimo caso otteniamo un quadrilatero inscritto ABDC. Quando si attraversa un cerchio, l'equazione dice che il prodotto delle lunghezze dei segmenti in cui si trova il punto X divide una diagonale è uguale al prodotto delle lunghezze dei segmenti in cui si trova il punto X divide l'altra diagonale. Questa condizione è nota come "teorema degli accordi intersecanti". Nel nostro caso le diagonali del quadrilatero inscritto sono le corde del cerchio.
Un altro criterio di ammissibilità. Quadrilatero convesso ABCD un cerchio è inscritto se e solo se

\tan(\frac(\alpha)(2))\tan(\frac(\gamma)(2))=\tan(\frac(\beta)(2))\tan(\frac(\delta)( 2))=1.

Criteri particolari per l'iscrizione di un quadrilatero

Un quadrilatero inscritto semplice (senza autointersezioni) è convesso. Una circonferenza può essere circoscritta ad un quadrilatero convesso se e solo se la somma dei suoi angoli opposti è 180° ( $\pi$ radiante). Puoi descrivere un cerchio attorno a:

qualsiasi antiparallelogramma
qualsiasi rettangolo (un caso speciale di quadrato)
qualsiasi trapezio isoscele
qualsiasi quadrilatero con due angoli opposti retti.

Proprietà

Formule con diagonali

ef=ac+bd

;

\frac(e)(f) = \frac(a\cdot d+b\cdot c)(a\cdot b+c\cdot d).

Nell'ultima formula della coppia di lati adiacenti del numeratore UN E D, B E C appoggiano le loro estremità su una diagonale di lunghezza e. Una affermazione simile vale per il denominatore.

Formule per le lunghezze diagonali(conseguenze ):

e = \sqrt(\frac((ac+bd)(ad+bc))(ab+cd))

f = \sqrt(\frac((ac+bd)(ab+cd))(ad+bc))

Formule con angoli

Per un quadrilatero inscritto con una sequenza di lati UN , B , C , D, con semiperimetro P e angolo UN tra le parti UN E D, funzioni trigonometriche dell'angolo UN sono dati da formule

$\cos A = \frac(a^2 + d^2 - b^2 - c^2)(2(ad + bc)),$ $\sin A = \frac(2\sqrt((p-a)(p-b)(p-c)(p-d)))((ad+bc)),$ $\tan \frac(A)(2) = \sqrt(\frac((p-a)(p-d))((p-b)(p-c))).$

Angolo θ tra le diagonali è :p.26

$\tan \frac(\theta)(2) = \sqrt(\frac((p-b)(p-d))((p-a)(p-c))).$

Se lati opposti UN E C si intersecano ad angolo φ , allora è uguale a

\cos(\frac(\varphi)(2))=\sqrt(\frac((p-b)(p-d)(b+d)^2)((ab+cd)(ad+bc))),

Dove Pè un semiperimetro. :p.31

Raggio di un cerchio circoscritto ad un quadrilatero

Formula di Parameshvara (Parameshvara)

Se un quadrilatero con lati consecutivi UN , B , C , D e semiperimetro Pè inscritto un cerchio, quindi lo è il suo raggio Formula Parameswar:P. 84

$R= \frac(1)(4) \sqrt(\frac((ab+cd)(ad+bc)(ac+bd))((p-a)(p-b)(p-c)(p-d))).$

Fu sviluppato dal matematico indiano Parameswar nel XV secolo (1380-1460 circa)

Un quadrilatero convesso (vedi figura a destra) formato da quattro dati diretto Mikel, è inscritto in un cerchio se e solo se il punto Miquel M del quadrilatero giace sulla retta che congiunge due dei sei punti di intersezione delle rette (quelli che non sono vertici del quadrilatero). Cioè, quando M giace su EF.

Criterio secondo cui un quadrilatero composto da due triangoli è inscritto in una circonferenza

f^2 = \frac((ac+bd)(ad+bc))((ab+cd)).

L'ultima condizione dà un'espressione per la diagonale F un quadrilatero inscritto in un cerchio, per la lunghezza dei suoi quattro lati ( UN, B, C, D). Questa formula segue immediatamente quando si moltiplicano e si equiparano tra loro le parti sinistra e destra delle formule che esprimono l'essenza Primo e secondo teorema di Tolomeo(vedi sopra).

Criterio secondo cui un quadrilatero tagliato da una retta da un triangolo è inscritto in una circonferenza

Una linea retta, antiparallela al lato del triangolo e che lo interseca, taglia da esso un quadrilatero, attorno al quale è sempre circoscrivibile un cerchio.
Conseguenza. In prossimità di un antiparallelogramma, in cui due lati opposti sono antiparalleli, è sempre possibile descrivere un cerchio.

Area di un quadrilatero inscritto in una circonferenza

Varianti della formula Brahmagupta

S=\sqrt((p-a)(p-b)(p-c)(p-d)),

dove p è il semiperimetro del quadrilatero.

S= \frac(1)(4) \sqrt(- \begin(vmatrix) a & b & c & -d \\ b & a & -d & c \\ c & -d & a & b \\ -d & c & b & a \end(vmatrix))

Altre formule di area

S = \tfrac(1)(2)(ab+cd)\sin(B)

S = \tfrac(1)(2)(ac+bd)\sin(\theta),

Dove θ uno qualsiasi degli angoli compresi tra le diagonali. A condizione che l'angolo UN non è diritta, l'area può anche essere espressa come :p.26

$S = \tfrac(1)(4)(a^2-b^2-c^2+d^2)\tan(A).$ $\displaystyle S=2R^2\sin(A)\sin(B)\sin(\theta),$

Dove Rè il raggio del cerchio circoscritto. Come diretta conseguenza abbiamo la disuguaglianza

$S\le 2R^2,$

dove l'uguaglianza è possibile se e solo se questo quadrilatero è un quadrato.

Quadrangoli di Brahmagupta

Quadrilatero Brahmaguptaè un quadrilatero inscritto in una circonferenza con lunghezze dei lati intere, diagonali intere e area intera. Tutti i possibili quadrilateri Brahmagupta con lati UN , B , C , D, con diagonali e , F, con superficie S e il raggio della circonferenza circoscritta R può essere ottenuto rimuovendo i denominatori delle seguenti espressioni che coinvolgono parametri razionali T , tu, E v :

$un=$ $b=(1+u^2)(v-t)(1+tv)$ $c=t(1+u^2)(1+v^2)$ $d=(1+v^2)(u-t)(1+tu)$ $e=u(1+t^2)(1+v^2)$ $f=v(1+t^2)(1+u^2)$ $S=uv$ $4R=(1+u^2)(1+v^2)(1+t^2).$

Esempi

I quadrilateri privati inscritti in una circonferenza sono: rettangolo, quadrato, trapezio isoscele o isoscele, antiparallelogramma.

Quadrilateri inscritti in una circonferenza con le diagonali perpendicolari (quadrilateri ortodiagonali inscritti)

Proprietà dei quadrilateri inscritti in una circonferenza con le diagonali perpendicolari

Raggio del cerchio circoscritto e area

Per un quadrilatero inscritto in una circonferenza con diagonali perpendicolari, supponiamo che l'intersezione delle diagonali divida una diagonale in segmenti di lunghezza P 1 e P 2 , e divide l'altra diagonale in segmenti di lunghezza Q 1 e Q 2. Quindi (La prima uguaglianza è la Proposizione 11 in Archimede " Libro dei Lemmi)

$D^2=p_1^2+p_2^2+q_1^2+q_2^2=a^2+c^2=b^2+d^2,$

Dove D- diametro del cerchio. Questo è vero perché le diagonali sono perpendicolari alla corda del cerchio. Da queste equazioni segue che il raggio del cerchio circoscritto R può essere scritto nella forma

$R=\tfrac(1)(2)\sqrt(p_1^2+p_2^2+q_1^2+q_2^2)$

o in termini di lati di un quadrilatero nella forma

$R=\tfrac(1)(2)\sqrt(a^2+c^2)=\tfrac(1)(2)\sqrt(b^2+d^2).$

Da ciò consegue anche che

$a^2+b^2+c^2+d^2=8R^2.$

Per i quadrilateri ortodiagonali inscritti, il teorema di Brahmagupta vale:

Se un quadrilatero inscritto ha le diagonali perpendicolari che si intersecano in un punto $M$ , quindi due paia di antimediatris passare per il punto $M$ .

Commento. In questo teorema, antimediatris comprendere il segmento $FE.$ quadrilatero nella figura a destra (per analogia con la bisettrice perpendicolare (mediatrice) al lato del triangolo). È perpendicolare a un lato e contemporaneamente passa per il punto medio del lato opposto del quadrilatero.

Scrivi una recensione sull'articolo "Quadangoli inscritti in un cerchio"

Appunti

Bradley, Christopher J. (2007), L'algebra della geometria: coordinate cartesiane, areali e proiettive, Alta percezione, pag. 179, ISBN 1906338000, OCLC
. Quadrilateri inscritti.
Siddons, AW e Hughes, RT (1929), Trigonometria, Cambridge University Press, pag. 202, OCLC
Durell, CV e Robson, A. (2003), Corriere Dover, ISBN 978-0-486-43229-8 ,
Alsina, Claudi & Nelsen, Roger B. (2007), "", Foro geometricorum T.7: 147–9 ,
Johnson, Roger A., Geometria euclidea avanzata, Dover Publ., 2007 (orig. 1929).
Hoehn, Larry (marzo 2000), "Circumradius di un quadrilatero ciclico", Gazzetta Matematica T.84 (499): 69–70
.
Altshiller-Court, Nathan (2007), Geometria universitaria: un'introduzione alla geometria moderna del triangolo e del cerchio(2a ed.), Courier Dover, ss. 131, 137–8, ISBN 978-0-486-45805-2, OCLC
Honsberger, Ross (1995), . Episodi di geometria euclidea dell'Ottocento e del Novecento, vol. 37, Nuova Biblioteca Matematica, Cambridge University Press, pp. 35–39, ISBN 978-0-88385-639-0
Weisstein, Eric W.(Inglese) sul sito web di Wolfram MathWorld.
Bradley, Christopher (2011), ,
.
Coxeter, Harold Scott MacDonald e Greitzer, Samuel L. (1967), . Geometria rivisitata, Associazione Matematica Americana, pp. 57, 60, ISBN 978-0-88385-619-2
.
Andreescu, Titu & Enescu, Bogdan (2004), . Tesori delle Olimpiadi della Matematica, Springer, ss. 44–46, 50, ISBN 978-0-8176-4305-8
.
Buchholz, RH e MacDougall, JA (1999), "", Bollettino della Società Matematica Australiana T.59(2): 263–9 , DOI 10.1017/S0004972700032883
.
Johnson, Roger A., Geometria euclidea avanzata, Dover Publ. co., 2007
, Con. 74.
.
.
.
Peter, Thomas (settembre 2003), "Massimizzare l'area di un quadrilatero", Il giornale di matematica del college T. 34 (4): 315–6
Prasolov, Viktor, ,
Alsina, Claudi & Nelsen, Roger (2009), , , Associazione Matematica d'America, p. 64, ISBN 978-0-88385-342-9 ,
Sastry, K.R.S. (2002). "" (PDF). Foro geometricorum 2 : 167–173.
Posamentier, Alfred S. & Salkind, Charles T. (1970), . Problemi impegnativi in geometria(2a ed.), Courier Dover, ss. 104–5, ISBN 978-0-486-69154-1
.
.
.

Guarda anche

Per numero di lati

corretto

triangoli

Quadrilateri

Guarda anche

L'articolo contiene brevi riferimenti ("Harvard") a pubblicazioni non elencate o descritte in modo errato nella sezione bibliografica.
Elenco dei collegamenti non funzionanti: , , , , , , , , , , - Ebbene, cosa, mio cosacco? (Marya Dmitrievna chiamava Natasha una cosacca) - disse, accarezzando Natasha con la mano, che si avvicinò alla sua mano senza paura e allegramente. - So che la pozione è una ragazza, ma la adoro.
Tirò fuori degli orecchini yakhon a forma di pera dal suo enorme reticolo e, dandoli a Natasha, che era raggiante e arrossata per il suo compleanno, si voltò immediatamente da lei e si rivolse a Pierre.
– Eh, eh! Tipo! vieni qui", disse con una voce beffardamente tranquilla e sottile. - Andiamo, mio caro...
E si rimboccò minacciosamente le maniche ancora più in alto.
Pierre si avvicinò, guardandola ingenuamente attraverso gli occhiali.
"Vieni, vieni, caro!" Ho detto la verità da solo a tuo padre, quando si trovava, e poi Dio te lo ha comandato.
Fece una pausa. Tutti tacevano, aspettando ciò che sarebbe successo e sentendo che c'era solo una prefazione.
- Va bene, niente da dire! bravo ragazzo!... Il padre si sdraia sul letto, e lui, divertito, mette la moneta ad un orso a cavallo. Vergognati, papà, vergognati! Meglio andare in guerra.
Lei si voltò e tese la mano al conte, che quasi non poté fare a meno di ridere.
- Bene, bene, a tavola, prendo il tè, è ora? disse Mar'ja Dmitrievna.
Il conte è andato avanti con Marya Dmitrievna; poi la contessa, guidata dal colonnello ussaro, la persona giusta con cui Nikolai avrebbe dovuto raggiungere il reggimento. Anna Mikhailovna è con Shinshin. Berg offrì la mano a Vera. Sorridendo, Julie Karagina andò con Nikolai al tavolo. Dietro di loro venivano altre coppie, allungate attraverso la sala, e dietro di loro, tutti soli, bambini, precettori e governanti. I camerieri si agitarono, le sedie tintinnarono, la musica risuonò negli stalli del coro e gli ospiti si sistemarono. I suoni della musica casalinga del conte furono sostituiti dai suoni di coltelli e forchette, dalle voci degli ospiti, dai passi silenziosi dei camerieri.
A un'estremità del tavolo sedeva a capotavola la contessa. A destra c'è Marya Dmitrievna, a sinistra c'è Anna Mikhailovna e altri ospiti. All'altra estremità sedeva il conte, a sinistra il colonnello ussaro, a destra Shinshin e altri ospiti maschi. Da un lato del lungo tavolo, i giovani più grandi: Vera accanto a Berg, Pierre accanto a Boris; dall'altra i bambini, i precettori e le governanti. Da dietro cristalli, bottiglie e vasi di frutta, il conte guardò la moglie e il suo alto berretto con nastri blu e versò diligentemente il vino ai vicini, senza dimenticare se stesso. Anche la contessa, a causa degli ananas, senza dimenticare i suoi doveri di padrona di casa, lanciò sguardi significativi al marito, la cui testa calva e il cui viso, le sembrava, si distinguevano nettamente dai capelli grigi per il loro rossore. Ci fu un regolare chiacchiericcio da parte delle donne; si sentivano voci sempre più forti sul maschio, soprattutto sul colonnello ussaro, che mangiava e beveva tanto, arrossendo sempre di più che il conte già lo dava da esempio agli altri ospiti. Berg, con un sorriso gentile, ha parlato con Vera del fatto che l'amore è un sentimento non terreno, ma celeste. Boris chiamò il suo nuovo amico Pierre con gli ospiti che erano a tavola e scambiò uno sguardo con Natasha, seduta di fronte a lui. Pierre parlava poco, guardava volti nuovi e mangiava molto. Partendo dalle due zuppe, tra le quali scelse à la tortue, [tartaruga] e kulebyaki, fino al gallo cedrone, non si lasciò sfuggire un solo piatto e non un solo vino, da cui il maggiordomo in una bottiglia avvolta in un tovagliolo sporgeva misteriosamente dalla spalla del suo vicino, dicendo o “drey Madeira, o ungherese, o vino del Reno”. Sostituì il primo dei quattro bicchieri di cristallo con il monogramma del conte, che stava davanti a ciascun apparecchio, e bevve con piacere, guardando gli ospiti sempre più piacevolmente. Natascia, seduta di fronte a lui, guardò Boris, come le ragazze di tredici anni guardano il ragazzo con cui si sono appena baciate per la prima volta e di cui sono innamorate. Questo suo stesso sguardo a volte si rivolgeva a Pierre, e sotto lo sguardo di quella ragazza divertente e vivace voleva ridere anche lui, senza sapere perché.
Nikolai era seduto lontano da Sonya, accanto a Julie Karagina, e di nuovo, con lo stesso sorriso involontario, le disse qualcosa. Sonya sorrise magnificamente, ma a quanto pare era tormentata dalla gelosia: impallidì, poi arrossì e con tutte le sue forze ascoltò quello che Nikolai e Julie si dicevano. La governante si guardò intorno a disagio, come se si preparasse a un rifiuto, se qualcuno avesse pensato di offendere i bambini. Il tutore tedesco cercò di memorizzare le categorie dei cibi, dei dolci e dei vini per descrivere tutto nei dettagli in una lettera alla sua famiglia in Germania, e rimase molto offeso dal fatto che il maggiordomo, con una bottiglia avvolta in un tovagliolo, circondasse lui. Il tedesco si accigliò, cercò di far vedere che non voleva ricevere questo vino, ma si offese perché nessuno voleva capire che aveva bisogno del vino non per dissetarsi, non per avidità, ma per coscienziosa curiosità.

All'estremità maschile del tavolo la conversazione si fece sempre più vivace. Il colonnello disse che il manifesto di guerra era già stato pubblicato a Pietroburgo e che la copia, che lui stesso aveva visto, era stata ora consegnata tramite corriere al comandante in capo.
- E perché è difficile per noi combattere con Bonaparte? Shinshin ha detto. - II a deja rabattu le caquet al "Autriche. Je crains, que cette fois ce ne soit notre tour. [Ha già abbattuto l'arroganza dell'Austria. Temo che il nostro turno non verrebbe adesso.]
Il colonnello era un tedesco robusto, alto e ottimista, ovviamente un attivista e un patriota. Era offeso dalle parole di Shinshin.
“E poi siamo un grasso sovrano”, ha detto, pronunciando e invece di e e b invece di b. "Allora, l'imperatore lo sa. Ha detto nel suo manifesto che non può guardare con indifferenza ai pericoli che minacciano la Russia, e che la sicurezza dell'impero, la sua dignità e la sacralità delle alleanze", ha detto, per qualche motivo particolarmente appoggiato sulla parola "sindacati", come se questa fosse tutta la questione.
E con la sua infallibile memoria ufficiale, ha ripetuto le parole introduttive del manifesto... “e il desiderio, obiettivo unico e imprescindibile del sovrano, è stabilire la pace in Europa su basi solide - hanno deciso di inviare parte dei esercito ora all’estero e compiere nuovi sforzi per raggiungere “questa intenzione”.
“Ecco perché, siamo un degno sovrano”, ha concluso, bevendo istruttivamente un bicchiere di vino e guardando indietro il conte per incoraggiarsi.
- Connaissez vous le proverbio: [Conosci il proverbio:] "Yerema, Yerema, se volessi sederti a casa, affila i tuoi fusi", disse Shinshin, sussultando e sorridendo. – Cela nous convient a merveille. [Questo è a proposito per noi.] Perché Suvorov - ed era diviso, un piatto couture, [sulla testa,] e dove sono adesso i nostri Suvorov? Je vous demande un peu, [vi chiedo] - saltava continuamente dal russo al francese, diceva.
"Dobbiamo combattere fino al giorno dopo la goccia di sangue", disse il colonnello, picchiando sul tavolo, "e morire per il nostro imperatore, e poi tutto andrà bene". E discutere il più possibile (soprattutto tirando fuori la voce sulla parola “possibile”), il meno possibile», concluse rivolgendosi nuovamente al conte. - Quindi giudichiamo i vecchi ussari, tutto qui. E come giudichi, giovane e giovane ussaro? - aggiunse rivolgendosi a Nikolai, il quale, sentendo che si trattava di guerra, lasciò il suo interlocutore e guardò con tutti gli occhi e ascoltò con tutte le orecchie il colonnello.
"Sono completamente d'accordo con te", rispose Nikolai, arrossendo tutto, girando il piatto e sistemando i bicchieri con uno sguardo così determinato e disperato, come se in questo momento fosse in grave pericolo, "sono convinto che i russi debbano morire o vincere", disse, sentendo lui stesso e gli altri, dopo che la parola era già stata detta, che era troppo entusiasta e pomposo per l'occasione attuale e quindi imbarazzante.
- C "est bien beau ce que vous venez de dire, [Magnifico! quello che hai detto è meraviglioso]," disse Julie, che era seduta accanto a lui, sospirando. Sonya tremò tutta e arrossì fino alle orecchie, dietro le orecchie e al collo e alle spalle, mentre Nikolai parlava, Pierre ascoltò i discorsi del colonnello e annuì in segno di approvazione.
"È carino", ha detto.
"Un vero ussaro, giovanotto", gridò il colonnello, colpendo di nuovo il tavolo.
- Di cosa stai parlando lì? All'improvviso si udì la voce bassa di Marya Dmitrievna dall'altra parte del tavolo. Perché sbatti sul tavolo? si rivolse all'ussaro: “per chi ti ecciti? vero, pensi che i francesi siano davanti a te?
"Dico la verità," disse l'ussaro sorridendo.
"È tutta una questione di guerra", gridò il conte dall'altra parte del tavolo. “Dopotutto, mio figlio verrà, Marya Dmitrievna, mio figlio verrà.
- E ho quattro figli nell'esercito, ma non mi addoloro. Tutto è la volontà di Dio: morirai sdraiato sui fornelli e Dio avrà pietà in battaglia ”, risuonò senza alcuno sforzo la voce spessa di Marya Dmitrievna, dall'altra estremità del tavolo.
- Questo è vero.
E la conversazione si concentrò di nuovo: le donne all'estremità del tavolo, gli uomini all'altra.
"Ma non lo chiederai", disse il fratellino a Natasha, "ma non lo chiederai!"
"Lo chiederò", rispose Natasha.
Il suo viso improvvisamente si infiammò, esprimendo una determinazione disperata e allegra. Si alzò a metà, invitando Pierre, che le era seduto di fronte, ad ascoltare con uno sguardo, e si rivolse a sua madre:
- Madre! la sua voce infantile risuonava per tutto il tavolo.
- Cosa vuoi? chiese spaventata la contessa, ma, vedendo dal volto della figlia che si trattava di uno scherzo, agitò severamente la mano, facendo con la testa un gesto minaccioso e negativo.
La conversazione si calmò.
- Madre! che torta sarà? - La voce di Natasha suonava ancora più risoluta, senza rompersi.
La Contessa avrebbe voluto accigliarsi, ma non poteva. Marya Dmitrievna scosse il grosso dito.
"Cosacco", disse minacciosamente.
La maggior parte degli ospiti guardò gli anziani, incerti su come affrontare questa acrobazia.
- Eccomi qui! disse la Contessa.
- Madre! quale sarà la torta? Natasha gridò già con audacia e capricciosamente allegramente, fiduciosa in anticipo che il suo trucco sarebbe stato ben accolto.
Sonya e la grassa Petya si nascondevano dalle risate.
"Così ho chiesto", sussurrò Natasha al fratellino e a Pierre, che guardò di nuovo.
"Gelato, ma non te lo daranno", ha detto Marya Dmitrievna.
Natasha vide che non c'era nulla di cui aver paura, e quindi non aveva paura nemmeno di Marya Dmitrievna.
— Mar'ja Dmitrievna? che gelato! Non mi piace il burro.
- Carota.
– No, cosa? Marya Dmitrievna, quale? quasi urlò. - Voglio sapere!
Mar'ja Dmitrievna e la contessa risero, seguite da tutti gli ospiti. Tutti hanno riso non della risposta di Marya Dmitrievna, ma dell'incomprensibile coraggio e destrezza di questa ragazza, che sapeva e ha osato trattare Marya Dmitrievna in questo modo.
Natasha rimase indietro solo quando le fu detto che ci sarebbe stato l'ananas. Lo champagne veniva servito prima del gelato. Di nuovo la musica cominciò a suonare, il conte baciò la contessa e gli ospiti, alzandosi, si congratularono con la contessa, brindarono con il conte, i bambini e tra di loro dall'altra parte del tavolo. Di nuovo i camerieri accorsero, le sedie tintinnarono, e nello stesso ordine, ma con le facce più rosse, gli ospiti tornarono nel salotto e nello studio del conte.

I tavoli di Boston furono spostati, furono organizzate feste e gli ospiti del conte furono sistemati in due soggiorni, un divano e una biblioteca.
Il conte, allargando le sue carte a ventaglio, difficilmente resisteva all'abitudine del pisolino pomeridiano e rideva di tutto. I giovani, incitati dalla contessa, si radunarono attorno al clavicordo e all'arpa. Julie è stata la prima, su richiesta di tutti, a suonare un brano con variazioni sull'arpa e, insieme ad altre ragazze, ha iniziato a chiedere a Natasha e Nikolai, noti per la loro musicalità, di cantare qualcosa. Natasha, che veniva chiamata grande, apparentemente ne era molto orgogliosa, ma allo stesso tempo era timida.
- Cosa canteremo? lei chiese.
"La chiave", rispose Nikolai.
- Beh, sbrighiamoci. Boris, vieni qui, - disse Natasha. - Dov'è Sonya?
Si guardò attorno e, vedendo che la sua amica non era nella stanza, le corse dietro.
Correndo nella stanza di Sonya e non trovando lì la sua amica, Natasha corse nella stanza dei bambini - e Sonya non c'era. Natasha si rese conto che Sonya era nel corridoio su una cassapanca. La cassapanca nel corridoio era il luogo dei dolori della giovane generazione femminile della casa di Rostov. Infatti, Sonya, nel suo arioso vestito rosa, schiacciandolo, si sdraiò a faccia in giù sul letto di piume dell'infermiera a strisce sporche, sul petto, e, coprendosi il viso con le dita, pianse amaramente, tremando con le spalle nude. Il viso di Natasha, vivace, per tutto il giorno, cambiò improvvisamente: i suoi occhi si fermarono, poi il suo ampio collo tremò, gli angoli delle sue labbra si abbassarono.
– Sonya! cosa sei?... Cosa, cosa ti succede? Woo-woo!...
E Natasha, allargando la sua grande bocca e diventando completamente brutta, ruggì come una bambina, non sapendo il motivo e solo perché Sonya piangeva. Sonya voleva alzare la testa, voleva rispondere, ma non poteva e si nascondeva ancora di più. Natasha piangeva, si sedeva su un piumino blu e abbracciava la sua amica. Raccogliendo le forze, Sonya si alzò, iniziò ad asciugarsi le lacrime e a raccontare.
- Nikolenka se ne andrà tra una settimana, il suo... foglio... è uscito... me lo ha detto lui stesso... sì, non piangerei... (mostra il foglio che tiene in mano: è era una poesia scritta da Nikolai) Io non piangerei, ma tu non puoi... nessuno può capire... che tipo di anima ha.
E ricominciò a piangere perché la sua anima era così buona.
"Ti fa bene... non invidio... ti amo, e anche Boris", disse, raccogliendo un po' le forze, "è carino... non ci sono ostacoli per te. E Nikolai è mio cugino... è necessario... lo stesso metropolita... e questo è impossibile. E poi, se mia madre ... (Sonya considerò la contessa e chiamò sua madre), dirà che rovino la carriera di Nikolai, non ho cuore, che sono ingrata, ma giusto ... per Dio ... ( (si fece il segno della croce) Anch'io la amo tanto, e tutti voi, solo Vera è una... Per cosa? Cosa le ho fatto? Ti sono così grato che sarei felice di sacrificare tutto, ma non ho niente...
Sonya non poteva più parlare e di nuovo nascose la testa tra le mani e il letto di piume. Natasha cominciò a calmarsi, ma dal suo viso era chiaro che comprendeva l'importanza del dolore della sua amica.
– Sonya! disse all'improvviso, come se indovinasse il vero motivo del dolore di sua cugina. "Giusto, Vera ti ha parlato dopo cena?" SÌ?
- Sì, Nikolai stesso ha scritto queste poesie e io ne ho cancellate altre; li trovò sul mio tavolo e disse che li avrebbe mostrati alla mamma, e disse anche che ero ingrato, che la mamma non gli avrebbe mai permesso di sposarmi, e lui avrebbe sposato Julie. Vedi come sta con lei tutto il giorno ... Natasha! Per quello?…
E ancora pianse amaramente. Natasha la sollevò, l'abbracciò e, sorridendo tra le lacrime, cominciò a consolarla.
“Sonya, non fidarti di lei, tesoro, no. Ricordi come abbiamo parlato tutti e tre con Nikolenka nella stanza del divano; ricordi dopo cena? Dopotutto, abbiamo deciso come sarà. Non ricordo come, ma ricordo come tutto andava bene e tutto è possibile. Il fratello di zio Shinshin è sposato con una cugina e noi siamo cugini di secondo grado. E Boris ha detto che è molto possibile. Sai, gli ho detto tutto. Ed è così intelligente e così bravo", disse Natasha ... "Tu, Sonya, non piangere, mia cara, cara, Sonya. E la baciò, ridendo. - La fede è cattiva, Dio sia con lei! E andrà tutto bene, e lei non lo dirà a sua madre; Nikolenka si dirà, e non ha nemmeno pensato a Julie.
E la baciò sulla testa. Sonya si alzò e il gattino si rianimò, i suoi occhi brillarono e sembrava pronto ad agitare la coda, saltare sulle sue zampe morbide e giocare di nuovo con la palla, come gli si conveniva.
- Si pensa? Giusto? Da Dio? disse, aggiustandosi rapidamente il vestito e i capelli.
- Giusto, per Dio! - rispose Natasha, lisciando alla sua amica sotto una falce una ciocca di capelli ruvidi caduta.
Ed entrambi risero.
- Bene, andiamo a cantare "Key".
- Andiamo a.
- E sai, questo grasso Pierre, che era seduto di fronte a me, è così divertente! disse all'improvviso Natasha, fermandosi. - Mi diverto molto!
E Natasha corse lungo il corridoio.
Sonya, spazzando via la lanugine e nascondendo le poesie nel seno, fino al collo con gli sterni sporgenti, con passi leggeri e allegri, con la faccia arrossata, corse dietro a Natasha lungo il corridoio fino al divano. Su richiesta degli ospiti, i giovani hanno cantato il quartetto "Key", che è piaciuto moltissimo a tutti; poi Nikolai ha cantato di nuovo la canzone che aveva imparato.
In una notte piacevole, al chiaro di luna,
Immagina di essere felice
Che c'è qualcun altro al mondo
Chi pensa anche a te!
Che lei, con una bella mano,
Camminando lungo l'arpa d'oro,
Con la sua appassionata armonia
Chiamando se stesso, chiamandoti!
Un altro giorno, due, e il paradiso arriverà...
Ma ah! il tuo amico non vivrà!
E non aveva ancora finito di cantare le ultime parole, quando nella sala i giovani si prepararono a ballare e i musicisti dei cori batterono i piedi e tossirono.

Pierre era seduto in soggiorno, dove Shinshin, come con un visitatore dall'estero, iniziò con lui una conversazione politica noiosa per Pierre, alla quale si unirono altri. Quando è iniziata la musica, Natasha è entrata nel soggiorno e, andando dritta verso Pierre, ridendo e arrossendo, ha detto:
“La mamma mi ha detto di chiederti di ballare.
"Ho paura di confondere le cifre", disse Pierre, "ma se vuoi essere il mio insegnante...
E diede la sua mano grossa, abbassandola verso la ragazza magra.
Mentre le coppie si preparavano e i musicisti costruivano, Pierre si sedette con la sua signorina. Natasha era perfettamente felice; ha ballato con un ragazzone che veniva dall'estero. Si sedette davanti a tutti e gli parlò come una grande. Aveva in mano un ventaglio, che una giovane donna le diede da tenere. E, adottando la posa più secolare (Dio sa dove e quando l'ha imparato), lei, sventolandosi con un ventaglio e sorridendo attraverso il ventaglio, ha parlato con il suo gentiluomo.
- Cos'è, cos'è? Guarda, guarda, - disse la vecchia contessa, attraversando l'atrio e indicando Natasha.
Natasha arrossì e rise.
- Beh, cosa sei, mamma? Bene, cosa stai cercando? Cosa c'è di sorprendente qui?

A metà della terza ecossaise, le sedie del salotto dove giocavano il conte e Mar'ja Dmitrievna cominciarono ad agitarsi, e la maggior parte degli ospiti d'onore e dei vecchi, stirandosi dopo una lunga seduta e infilando portafogli e borsette dalle loro tasche, uscirono dalle porte della sala. Mar'ja Dmitrievna camminava davanti al conte, entrambi con la faccia allegra. Con giocosa gentilezza, come in un balletto, il conte tese la mano rotonda a Marya Dmitrievna. Si raddrizzò, il suo viso si illuminò di un sorriso particolarmente coraggioso e malizioso, e non appena fu ballata l'ultima figura dell'ecosaise, batté le mani ai musicisti e gridò ai cori, rivolgendosi al primo violino:
- Semyon! Conosci Danila Kupor?
Era la danza preferita del conte, ballata da lui in gioventù. (Danilo Kupor era in realtà una figura anglaise.)
"Guarda papà", gridò Natasha a tutta la sala (dimenticando completamente che stava ballando con un grande), piegando la testa riccia sulle ginocchia e scoppiando con la sua risata sonora in tutta la sala.
In effetti, tutti nella sala guardarono con un sorriso di gioia l'allegro vecchio che, accanto alla sua dignitaria, Marya Dmitrievna, che era più alta di lui, arrotolò le braccia, scuotendole a tempo, raddrizzò le spalle, girò le braccia gambe, battendo leggermente i piedi, e con un sorriso sempre più sbocciante sul viso tondo preparava il pubblico per quello che sarebbe successo. Non appena si udirono i suoni allegri e provocatori di Danila Kupor, simili a un allegro sonaglio, tutte le porte della sala furono improvvisamente forzate da un lato da volti maschili, dall'altro da volti femminili sorridenti dei cortili che uscivano a guardare all'allegro gentiluomo.
- Il padre è nostro! Aquila! disse ad alta voce la tata da una porta.
Il conte ballava bene e lo sapeva, ma la sua dama non sapeva e non voleva ballare bene. Il suo corpo enorme stava ritto con le braccia potenti pendenti (consegnò la borsa alla contessa); solo il suo viso severo ma bello danzava. Ciò che era espresso nell'intera figura rotonda del conte, con Marya Dmitrievna si esprimeva solo in un viso sempre più sorridente e in un naso che si contraeva. Ma d'altra parte, se il conte, sempre più dispersivo, affascinava il pubblico con l'inaspettata di abili acrobazie e salti leggeri delle sue gambe morbide, Marya Dmitrievna, con il minimo zelo nel muovere le spalle o nell'arrotondare le braccia a turno e il calpestio, non fece meno impressione nel merito, che fu apprezzato da tutti per la sua corpulenza e la severità eterna. La danza divenne sempre più vivace. Le controparti non sono riuscite ad attirare l'attenzione su di sé per un minuto e non hanno nemmeno provato a farlo. Tutto era occupato dal conte e da Marya Dmitrievna. Natasha ha tirato le maniche e i vestiti di tutti i presenti, che già non distoglievano lo sguardo dai ballerini, e ha chiesto loro di guardare papà. Durante gli intervalli del ballo, il conte faceva un respiro profondo, salutava e gridava ai musicisti di suonare più velocemente. Sempre più veloce, sempre più veloce, sempre di più, il conte si aprì, ora in punta di piedi, ora sui talloni, correndo attorno a Marya Dmitrievna e, infine, voltando la sua signora al suo posto, fece l'ultimo passo, sollevando la gamba morbida verso l'alto da dietro, chinando la testa sudata con una faccia sorridente e agitando la mano destra in mezzo allo scroscio di applausi e risate, soprattutto Natasha. Entrambi i ballerini si fermarono, respirando affannosamente e asciugandosi con fazzoletti di batista.
"Così ballavano ai nostri tempi, ma chere", disse il conte.
- Oh sì, Danila Kupor! - disse Mar'ja Dmitrievna, respirando pesantemente e continuamente e rimboccandosi le maniche.

Mentre nella sala dei Rostov si ballava il sesto inglese al suono di musicisti stanchi e stonati, e i camerieri e i cuochi stanchi preparavano la cena, il sesto colpo ebbe luogo con il conte Bezukhim. I medici hanno annunciato che non c'erano speranze di guarigione; al paziente è stata data una confessione e una comunione sorda; si facevano i preparativi per l'unzione, e la casa era piena del trambusto e dell'ansia dell'attesa, comuni in quei momenti. Fuori casa, dietro i cancelli, si affollavano le pompe funebri, nascondendosi dalle carrozze che si avvicinavano, in attesa di un ricco ordine per i funerali del conte. Il comandante in capo di Mosca, che inviava costantemente aiutanti per conoscere la posizione del conte, quella sera venne lui stesso a salutare il famoso nobile di Caterina, il conte Bezukhim.
La magnifica sala dei ricevimenti era piena. Tutti si alzarono rispettosamente in piedi quando il comandante in capo, rimasto solo con il malato per circa mezz'ora, se ne andò, rispondendo lievemente agli inchini e cercando al più presto di sfuggire agli occhi fissi di medici, chierici e parenti lui. Il principe Vasily, che in questi giorni era diventato più magro e pallido, salutò il comandante in capo e gli ripeté tranquillamente qualcosa più volte.
Dopo aver salutato il comandante in capo, il principe Vasily si sedette da solo nella sala su una sedia, gettando le gambe in alto sopra le gambe, appoggiando il gomito sul ginocchio e chiudendo gli occhi con la mano. Dopo essere rimasto seduto così per un po', si alzò e con passi insolitamente affrettati, guardandosi attorno con occhi spaventati, attraversò un lungo corridoio fino alla metà posteriore della casa, dalla principessa più anziana.
Coloro che erano nella stanza poco illuminata parlavano tra loro in un sussurro irregolare e ogni volta tacevano, e con occhi pieni di domande e di aspettativa guardavano indietro verso la porta che conduceva alle camere del morente ed emettevano un debole suono quando qualcuno l'ha lasciato o è entrato.
“Il limite umano”, disse il vecchio, un sacerdote, alla signora che si sedette accanto a lui e lo ascoltò ingenuamente, “il limite è fissato, ma non si può oltrepassarlo”.
– Penso che non sia troppo tardi per l’unzione? - aggiungendo un titolo spirituale, chiese la signora, come se non avesse alcuna opinione al riguardo.

"Cerchio circoscritto" abbiamo visto che un cerchio può essere circoscritto attorno a qualsiasi triangolo. Cioè, per ogni triangolo esiste un cerchio tale che tutti e tre i vertici del triangolo "siedono" su di esso. Come questo:

Domanda: Si può dire lo stesso di un quadrilatero? È vero che ci sarà sempre un cerchio su cui “siederanno” tutti e quattro i vertici del quadrilatero?

Si scopre che questo NON È VERO! NON SEMPRE un quadrilatero può essere inscritto in un cerchio. C'è una condizione molto importante:

Nel nostro disegno:

Guarda, gli angoli e si trovano uno di fronte all'altro, il che significa che sono opposti. E allora gli angoli? Sembrano anche loro opposti? È possibile prendere gli angoli e invece degli angoli e?

Certo che puoi! La cosa principale è che il quadrilatero ha circa due angoli opposti, la cui somma sarà. Anche i restanti due angoli si sommeranno. Non credere? Assicuriamoci. Aspetto:

Lascia stare. Ricordi qual è la somma di tutti e quattro gli angoli di un quadrilatero? Certamente, . Cioè - sempre! . Ma → .

Magia direttamente!

Quindi ricorda con fermezza:

Se un quadrilatero è inscritto in una circonferenza, allora la somma di due qualsiasi dei suoi angoli opposti lo è

e viceversa:

Se un quadrilatero ha due angoli opposti la cui somma è uguale, allora tale quadrilatero è inscritto.

Non dimostreremo tutto questo qui (se sei interessato, guarda i livelli successivi della teoria). Ma vediamo a cosa porta questo meraviglioso fatto, che la somma degli angoli opposti di un quadrilatero inscritto è uguale.

Ad esempio, mi viene in mente la domanda: è possibile descrivere un cerchio attorno a un parallelogramma? Proviamo prima il "metodo poke".

In qualche modo non funziona.

Ora applica la conoscenza:

supponiamo che in qualche modo siamo riusciti a adattare un cerchio a un parallelogramma. Allora deve certamente essere:, cioè.

E ora ricordiamo le proprietà di un parallelogramma:

Ogni parallelogramma ha gli angoli opposti.

Abbiamo capito

E per quanto riguarda gli angoli? Beh, lo stesso ovviamente.

Iscritto → →

Parallelogramma→ →

Incredibile, vero?

Si è scoperto che se un parallelogramma è inscritto in un cerchio, allora tutti i suoi angoli sono uguali, cioè è un rettangolo!

E allo stesso tempo - il centro del cerchio coincide con il punto di intersezione delle diagonali di questo rettangolo. Questo, per così dire, è allegato come bonus.

Bene, questo significa che abbiamo scoperto che un parallelogramma inscritto in un cerchio... rettangolo.

Ora parliamo del trapezio. Cosa succede se un trapezio è inscritto in una circonferenza? E si scopre che lo farà trapezio isoscele. Perché?

Lascia che il trapezio sia inscritto in un cerchio. Poi di nuovo, ma a causa del parallelismo delle linee e.

Abbiamo quindi: → → un trapezio isoscele.

Ancora più facile che con un rettangolo, giusto? Ma devi ricordare con fermezza: torna utile:

Elenchiamo i più affermazioni principali tangente ad un quadrilatero inscritto in una circonferenza:

Un quadrilatero è inscritto in una circonferenza se e solo se la somma dei suoi due angoli opposti lo è
Parallelogramma inscritto in una circonferenza rettangolo e il centro del cerchio coincide con il punto di intersezione delle diagonali
Un trapezio inscritto in una circonferenza è isoscele.

Quadrilatero inscritto. Livello medio

È noto che per ogni triangolo esiste un cerchio circoscritto (lo abbiamo dimostrato nell'argomento “Cerchio circoscritto”). Cosa si può dire del quadrilatero? Ecco che si scopre NON TUTTI I quadrilateri possono essere inscritti in una circonferenza, ma esiste questo teorema:

Un quadrilatero è inscritto in una circonferenza se e solo se lo è la somma degli angoli opposti.

Nel nostro disegno -

Proviamo a capire perché? In altre parole, dimostreremo ora questo teorema. Ma prima di dimostrarlo, devi capire come funziona l'affermazione stessa. Hai notato le parole "allora e solo allora" nella dichiarazione? Tali parole significano che i matematici dannosi hanno condensato due affermazioni in una sola.

Decifrare:

"Allora" significa: se un quadrilatero è inscritto in un cerchio, allora la somma di due qualsiasi dei suoi angoli opposti è uguale.
“Solo allora” significa: se un quadrilatero ha due angoli opposti, la cui somma è uguale, allora tale quadrilatero può essere inscritto in un cerchio.

Proprio come Alice: “Penso quello che dico” e “Dico quello che penso”.

Ora scopriamo perché sia 1 che 2 sono veri?

Primo 1.

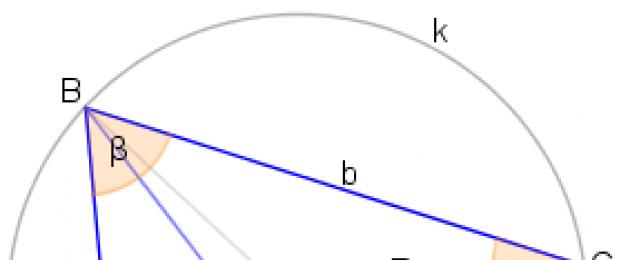
Sia inscritto il quadrilatero in una circonferenza. Ne segniamo il centro e disegniamo i raggi e. Cosa accadrà? Ricordi che un angolo inscritto è la metà del corrispondente angolo al centro? Se ricordi, ora è applicabile e, in caso contrario, guarda l'argomento "Cerchio. Angolo inscritto".

Iscritto

Ma guarda: .

Lo capiamo se - è scritto, allora

Bene, questo è chiaro e anche i conti tornano. (dovrebbe anche essere considerato).

Ora il “viceversa”, cioè 2.

Risulta che la somma di due angoli opposti qualsiasi di un quadrilatero sia uguale. Diciamo lasciamo

Non sappiamo ancora se possiamo descrivere un cerchio attorno ad esso. Ma sappiamo per certo che siamo in grado di descrivere un cerchio attorno a un triangolo. Facciamolo.

Se il punto non si "sedeva" sul cerchio, inevitabilmente si trovava all'esterno o all'interno.

Consideriamo entrambi i casi.

Lasciamo che il punto sia prima all'esterno. Quindi il segmento interseca il cerchio ad un certo punto. Connetti e. Il risultato è un quadrilatero inscritto (!).

Sappiamo già di lui che la somma dei suoi angoli opposti è uguale, cioè, ma a condizione che abbiamo.

Si scopre che dovrebbe essere così.

Ma questo non può essere in alcun modo, poiché - l'angolo esterno per e significa .

E dentro? Facciamo una cosa simile. Lasciamo il punto dentro.

Quindi la continuazione del segmento interseca il cerchio in un punto. Ancora una volta - un quadrilatero inscritto, e secondo la condizione deve essere soddisfatto, ma - un angolo esterno per e significa, cioè, ancora una volta, non può essere quello.

Cioè, un punto non può trovarsi né all'esterno né all'interno del cerchio, il che significa che si trova sul cerchio!

Dimostrato l'intero teorema!

Vediamo ora quali buone conseguenze dà questo teorema.

Corollario 1

Un parallelogramma inscritto in una circonferenza può essere solo un rettangolo.

Capiamo perché. Lascia che il parallelogramma sia inscritto in una circonferenza. Allora dovrebbe essere fatto.

Ma dalle proprietà di un parallelogramma, lo sappiamo.

E lo stesso, ovviamente, per gli angoli e.

Quindi è risultato il rettangolo: tutti gli angoli sono lungo.

Ma c'è anche un altro fatto piacevole: il centro del cerchio circoscritto al rettangolo coincide con il punto di intersezione delle diagonali.

Capiamo perché. Spero che tu ricordi molto bene che l'angolo basato sul diametro è un angolo retto.

Diametro,

Diametro

e quindi il centro. È tutto.

Conseguenza 2

Un trapezio inscritto in una circonferenza è isoscele.

Lascia che il trapezio sia inscritto in un cerchio. Poi.

E anche.

Abbiamo discusso di tutto? Non proprio. Esiste infatti un altro modo, "segreto", per riconoscere un quadrilatero inscritto. Formuleremo questo metodo in modo non molto rigoroso (ma chiaro), ma lo dimostreremo solo nell'ultimo livello della teoria.

Se in un quadrilatero si può osservare un'immagine come quella qui in figura (qui gli angoli “guardano” dal lato dei punti e sono uguali), allora tale quadrilatero è inscritto.

Questo è un disegno molto importante: nei problemi spesso è più facile trovare angoli uguali che la somma degli angoli e.

Nonostante la completa mancanza di rigore nella nostra formulazione, essa è corretta e, inoltre, è sempre accettata dagli esaminatori USE. Dovresti scrivere così:

“- inscritto” - e tutto andrà bene!

Non dimenticare questo segno importante: ricorda l'immagine e forse attirerà la tua attenzione in tempo quando risolverai il problema.

Quadrilatero inscritto. Breve descrizione e formule base

Se un quadrilatero è inscritto in una circonferenza, allora la somma di due qualsiasi dei suoi angoli opposti lo è

e viceversa:

Se un quadrilatero ha due angoli opposti la cui somma è uguale, allora tale quadrilatero è inscritto.

Un quadrilatero è inscritto in una circonferenza se e solo se la somma dei suoi due angoli opposti è uguale.

Parallelogramma inscritto in una circonferenza- necessariamente un rettangolo e il centro del cerchio coincide con il punto di intersezione delle diagonali.

Un trapezio inscritto in una circonferenza è isoscele.

Un quadrilatero è inscritto in un cerchio (compiti). Continuiamo a considerare i compiti che fanno parte dell'esame di matematica. In questo articolo risolveremo diversi problemi utilizzando le proprietà di un angolo inscritto. La teoria è già stata spiegata in dettaglio. In questo articolo, la soluzione dei compiti si riduceva essenzialmente all'applicazione immediata della proprietà dell'angolo inscritto, ovvero questi erano compiti quasi in un unico passaggio. Qui bisogna pensarci un po', il corso della decisione non è sempre immediatamente ovvio.

Applicare: il teorema sulla somma degli angoli di un triangolo, le proprietà dell'angolo inscritto, la proprietà del quadrilatero inscritto in una circonferenza. Maggiori informazioni su quest'ultimo.

*Questo immobile è già stato presentato, ma in una diversa interpretazione. COSÌ:

Proprietà:

Un quadrilatero inscritto è un quadrilatero i cui vertici giacciono tutti sulla stessa circonferenza.
Un quadrilatero può essere inscritto in una circonferenza se e solo se la somma degli angoli opposti è 180 gradi.

Cioè, se siamo un quadrilatero, la somma dei suoi angoli opposti è 180 gradi.

Considera i compiti:

27870. In un cerchio con un centro O AC E B.D- diametri. Angolo centrale AODè uguale a 110 0 . Trova un angolo inscritto ACB. Dai la tua risposta in gradi.

Triangolo Bsistema operativo isoscele, perché OS=OB(questi sono i raggi). Sappiamo che la somma degli angoli di un triangolo è 180 gradi. Consideriamo ∠BOC e ∠AOD:

Quindi

Gli angoli alla base di un triangolo isoscele sono cioè uguali

Un altro modo:

L'angolo AOB è l'angolo al centro dell'angolo inscritto ACB.Secondo la proprietà dell'angolo inscritto in una circonferenza

La somma degli angoli adiacenti è 180 0, quindi

Così

Risposta: 35

27871. L'angolo A del quadrilatero ABCD inscritto in una circonferenza è 58 0 . Trova l'angolo C di questo quadrilatero. Dai la tua risposta in gradi.

Qui basta ricordare la proprietà di tale quadrilatero. È noto che la somma dei suoi angoli opposti è pari a 180 gradi, il che significa che l'angolo C sarà pari a

Secondo modo:

Costruiamo OB e OD.

Per la proprietà dell'angolo inscritto, il valore in gradi dell'arco BCD è uguale a

2∙58 0 = 116 0

Pertanto, il valore in gradi dell'arco BAD sarà uguale a

360 0 – 116 0 = 244 0

Secondo la proprietà dell'angolo inscritto, l'angolo C sarà la metà, cioè 122 0.

Risposta: 122

27872. Lati di un quadrilatero ABCD AB, AVANTI CRISTO, CD E ANNO DOMINI contrarre gli archi di cerchio circoscritto, i cui valori in gradi sono rispettivamente 95 0 , 49 0 , 71 0 , 145 0 . Trova un angolo B questo quadrilatero. Dai la tua risposta in gradi.

Costruiamo i raggi AO, OD, OC:

Il valore in gradi dell'arco AD è 145 0 , il valore in gradi dell'arco CD è 71 0 , quindi il valore in gradi dell'arco ADC è 145 0 + 71 0 = 216 0 .

Secondo la proprietà dell'angolo inscritto, l'angolo B sarà la metà dell'angolo al centro corrispondente all'arco ADC

Risposta: 108

27874. Quadrilatero ABCD inscritto in un cerchio. Angolo ABC uguale a 105 0 , angolo CADè uguale a 35 0 . Trova un angolo ABD. Dai la tua risposta in gradi.

Questo compito può essere difficile. Non è immediatamente possibile vedere chiaramente lo stato di avanzamento della soluzione. Ricordiamo ciò che sappiamo di un quadrilatero inscritto: la somma dei suoi angoli opposti è 180 gradi. Cerchiamo

Per il momento abbiamo trovato l'angolo che può essere immediatamente determinato mediante una proprietà nota. Se c'è un'opportunità per trovare valore, fallo, ti tornerà utile. Agiamo secondo il principio “troviamo ciò che può essere trovato in base ai valori dati”.

Gli angoli inscritti ABD e ACD si basano sullo stesso arco, il che significa che sono uguali, cioè

Risposta: 70

27875. Quadrilatero ABCD inscritto in un cerchio. Angolo ABD uguale a 75 0 , angolo CADè uguale a 35 0 . Trova un angolo ABC. Dai la tua risposta in gradi.

È noto che gli angoli inscritti basati sullo stesso arco e giacenti dalla stessa parte sono uguali. Quindi

Nel triangolo ACD si conoscono due angoli, il terzo lo possiamo trovare:

Noto che è importante ricordare queste proprietà e compiti che risolverai senza problemi. Naturalmente, è possibile costruire una soluzione non del tutto corretta. Ad esempio, nel problema 27876, per una soluzione indipendente viene fornita una soluzione "lunga" o, come si suol dire, irrazionale. Va bene se risolvi anche il problema.

La cosa principale è ricordare e applicare la teoria e alla fine DECIDERE il compito.

In questa sezione continueremo a considerare i compiti, ti invito al blog!

È tutto. Buona fortuna a te!

Cordiali saluti, Alexander Krutitskikh

La commissione chiede al direttore di una semplice scuola rurale:
- Per quale motivo tutti i tuoi figli dicono: venuti, andati?
— E chissà, forse sono così abituati!

P.S: ti sarei grato se parlassi del sito nei social network.

poligoni inscritti e circoscritti,

§ 106. PROPRIETÀ DEI QUADRANGOLI INSCRITTI E CIRCONDATI.

Teorema 1. La somma degli angoli opposti di un quadrilatero inscritto è 180°.

Sia inscritto in un cerchio di centro O il quadrilatero ABCD (Fig. 412). È necessario dimostrarlo / A+ / C = 180° e / B+ / D = 180°.

/ A, come inscritto nel cerchio O, misura 1/2 BCD.
/ C, come inscritto nello stesso cerchio, misura 1/2 BAD.

Pertanto la somma degli angoli A e C è misurata dalla metà della somma degli archi BCD e BAD; in totale questi archi formano un cerchio, cioè hanno 360°.
Da qui / A+ / C = 360°: 2 = 180°.

Allo stesso modo, è dimostrato / B+ / D = 180°. Tuttavia, questo può essere ricavato anche in un altro modo. Sappiamo che la somma degli angoli interni di un quadrilatero convesso è 360°. La somma degli angoli A e C è 180°, ciò significa che anche la somma degli altri due angoli del quadrilatero rimane 180°.

Teorema 2(inversione). Se la somma di due angoli opposti in un quadrilatero è 180° , allora attorno a tale quadrilatero si può circoscrivere un cerchio.

Sia la somma degli angoli opposti del quadrilatero ABCD pari a 180°
/ A+ / C = 180° e / B+ / D = 180° (Fig. 412).

Dimostriamo che attorno a tale quadrilatero è possibile circoscrivere un cerchio.

Prova. Un cerchio può essere tracciato attraverso 3 vertici qualsiasi di questo quadrilatero, ad esempio attraverso i punti A, B e C. Dove si troverà il punto D?

Il punto D può assumere solo una delle seguenti tre posizioni: essere all'interno del cerchio, essere all'esterno del cerchio, essere sulla circonferenza del cerchio.

Supponiamo che il vertice sia interno al cerchio e assuma la posizione D” (Fig. 413). Allora nel quadrilatero ABCD” avremo:

/ B+ / D" = 2 D.

Proseguendo il lato AD" fino all'intersezione con il cerchio nel punto E e congiungendo i punti E e C, si ottiene il quadrilatero inscritto ABCE, nel quale, secondo il teorema diretto

/ B+ / E = 2 D.

Da queste due uguaglianze segue:

/ D" = 2 D - / B;
/ E=2 D - / B;

/ D"= / E,

ma questo non può essere, perché / D", essendo esterno al triangolo CD"E, deve essere maggiore dell'angolo E. Pertanto il punto D non può essere interno al cerchio.

È inoltre dimostrato che il vertice D non può occupare la posizione D" all'esterno del cerchio (fig. 414).

Resta da riconoscere che il vertice D deve giacere sulla circonferenza del cerchio, cioè coincidere con il punto E, il che significa che un cerchio può essere circoscritto vicino al quadrilatero ABCD.

Conseguenze. 1. Un cerchio può essere circoscritto attorno a qualsiasi rettangolo.

2. Una circonferenza può essere circoscritta attorno ad un trapezio isoscele.

In entrambi i casi la somma degli angoli opposti è 180°.

Teorema 3. Nel quadrilatero circoscritto le somme dei lati opposti sono uguali. Sia circoscritto ad un cerchio il quadrilatero ABCD (fig. 415), cioè i suoi lati AB, BC, CD e DA siano tangenti a questo cerchio.

Occorre dimostrare che AB + CD = AD + BC. Indichiamo i punti di contatto con le lettere M, N, K, P. Basandoci sulle proprietà delle tangenti tracciate su un cerchio da un punto (§ 75), abbiamo:

AR = AK;
PA=VM;
DN=DK;
CN=CM.

Sommiamo queste uguaglianze termine per termine. Noi abbiamo:

AR + BP + DN + CN = AK + BM + DK + SM,

cioè AB + CD = AD + BC, che doveva essere dimostrato.

Esercizi.

1. In un quadrilatero inscritto, due angoli opposti sono correlati come 3: 5,
e gli altri due sono correlati come 4: 5. Determina la grandezza di questi angoli.

2. Nel quadrilatero descritto, la somma di due lati opposti è 45 cm, i restanti due lati sono correlati come 0,2: 0,3. Trova la lunghezza di questi lati.

totale:0
In contatto con 0
Google Plus 0
OK 0
Facebook 0