Introduzione alla matematica. Ordini stabili sul semigruppo moltiplicativo dei numeri naturali Ordinamento dell'insieme dei numeri naturali

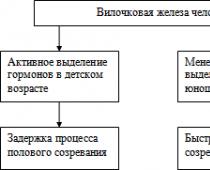
Kabirov Nikolai Nikolaevich, studente del secondo anno della Facoltà di Fisica, Matematica, Informatica, Istituto Taganrog intitolato ad A.P. [e-mail protetta]

Lyakhova Natalya Evgenievna, candidata di scienze fisiche e matematiche, capo del dipartimento di matematica, Istituto Taganrog intitolato ad A.P. [e-mail protetta]

Ordini stabili sul semigruppo moltiplicativo dei numeri naturali

Riassunto L'articolo è dedicato alla descrizione di tutti i modi possibili per specificare l'ordine su un semigruppo di numeri naturali mediante moltiplicazione o addizione, che hanno la proprietà di stabilità.Parole chiave: relazione d'ordine, algebra universale dei numeri naturali, relazione stabile.

In questo articolo considereremo sistemi algebrici in cui l'insieme principale è l'insieme dei numeri naturali, le operazioni sono l'addizione e la moltiplicazione e la relazione è la relazione d'ordine, che è associata alle operazioni dalla proprietà di stabilità. Sorge un problema naturale descrivere tutti i modi possibili per specificare l'ordine nell'algebra universale dei numeri naturali mediante moltiplicazione o addizione, che avrebbero la proprietà di stabilità. Esempi ben noti di queste relazioni d'ordine sono le relazioni di confronto dei numeri in grandezza e la relazione di divisibilità. Si scopre che non sono gli unici, esiste un numero infinito di tali ordini. Nell'articolo vengono indicati esplicitamente tutti gli ordini stabili nei semigruppi moltiplicativi e additivi dei numeri naturali e come esempio di tali ordini vengono forniti gli ordini generati da un insieme di coppie coprime.

1. Definizioni di base

Una relazione binaria su un insieme è un sottoinsieme di un prodotto cartesiano. Se, dove, allora scriveremo e diremo “cosa è in relazione a”. Un tipo importante di relazioni binarie sono le relazioni di ordinamento parziale, cioè relazioni binarie che hanno le proprietà di riflessività, transitività e antisimmetria. Un insieme con un dato ordine parziale si dice parzialmente ordinato. Per scrivere l'ordinamento, solitamente viene utilizzato un simbolo; se e, allora, a seconda delle circostanze, si dice che è minore o uguale a, è contenuto in, precede b. Si dia nell'insieme un ordinamento parziale. Gli elementi e questo insieme saranno chiamati comparabili, se o. Due elementi non devono assolutamente essere confrontabili: è per questo motivo che si può parlare di ordinamento “parziale”. In questo modo si ottiene un banale ordinamento parziale di un insieme, se assumiamo che solo se elementi diversi da saranno incomparabili. Un insieme parzialmente ordinato in cui due elementi qualsiasi sono confrontabili è chiamato insieme ordinato o insieme ordinato linearmente o catena In vari rami della matematica, gli insiemi ordinati e parzialmente ordinati ricorrono con estrema frequenza. Esempi di insiemi ordinati includono l'insieme dei numeri naturali e l'insieme dei numeri reali, entrambi nel loro ordine naturale. Esempi di insiemi parzialmente (ma non linearmente) ordinati sono i seguenti insiemi:

di tutti i sottoinsiemi di un insieme dato con la relazione di inclusione teorica degli insiemi come relazione di ordinamento parziale; è l'insieme di tutte le funzioni reali continue definite su un segmento, se significa che per tutti; è l'insieme di tutti i numeri naturali, se inteso nel senso che è diviso interamente da Un ordine su un semigruppo è un ordine parziale che soddisfa la condizione di stabilità

Un semigruppo in cui è definito un ordine parziale stabile rispetto all'operazione è detto semigruppo ordinato. Ovviamente qualunque semigruppo può considerarsi ordinato rispetto all'ordine banale. Come esempi di ordini parzialmente stabili, possiamo citare gli ordini di cui sopra su un semigruppo e su un semigruppo.Come segue dalle definizioni, un ordine è una relazione binaria, cioè molte coppie. Ciò dà origine a un metodo per descrivere tutti gli ordini parziali su un semigruppo. Chiameremo un ordine generato da un insieme di coppie se è l'ordine minimo contenente questo insieme di coppie. Se è possibile trovare una forma generale dell'ordine generato da un insieme arbitrario di coppie, questa sarà la soluzione del problema. È chiaro che non per ogni insieme di coppie viene generato un ordine: ovviamente un insieme non può generare un ordine.

2. Ordini su N,  generati da un insieme finito di coppie

È facile vedere che ciascuna coppia di numeri naturali può essere rappresentata come dove n è un numero naturale e q è una frazione positiva. Ad esempio, è possibile registrare una coppia. Permettere

un sottoinsieme finito arbitrario di un quadrato cartesiano. Quindi, secondo quanto sopra, può essere rappresentato come:

Definizione. Un insieme di coppie sarà detto antisimmetrico se contiene qualsiasi insieme di numeri dell'insieme

Allo stesso tempo non uguale a zero, È chiaro che la definizione è una generalizzazione del noto concetto di antisimmetria.

Definizione Let

insieme di coppie antisimmetriche. Qualsiasi numero naturale per il quale esistono due sequenze di questo tipo, dove e dove tale che,

Dove il primo numero di una coppia del set è chiamato numero e i numeri

impostare i numeri.

Teorema 1. Se

un insieme finito antisimmetrico di coppie, allora una relazione binaria tale che se e solo se o è un numero ed è un numero dell'insieme, è l'ordine generato da questo insieme.

Prova. Per dimostrare il teorema è necessario mostrare che, in primo luogo, la relazione d’ordine, e, in secondo luogo,

coincide con l'ordine generato dall'insieme.

Dimostriamo la prima parte del teorema, cioè prova che

è riflessivo, transitivo, antisimmetrico e stabile rispetto alla moltiplicazione.1) La riflessività segue dalla definizione della relazione.2) Sia

E. Dalla condizione che abbiamo

E dalla condizione che abbiamo

Pertanto, per uno si possono specificare due sequenze

e, in modo tale che,

Quelli. -numero e -numero del set. Quindi. Casi in cui o sono evidenti. La transitività è dimostrata. 3) Sia e. Consegue dalla condizione che. Consegue dalla condizione che.

e allo stesso tempo Poiché tutto, queste uguaglianze possono essere scritte nella forma

Dall'ultima uguaglianza segue che Ma questo è possibile solo per , poiché l’insieme è antisimmetrico. Considerando questo e, otteniamo Quindi. L'antisimmetria è dimostrata 4) La stabilità alla moltiplicazione consegue ovviamente dalla stabilità della relazione di uguaglianza, che serve per determinare i numeri dell'insieme.Dimostriamo la seconda parte del teorema. Denotare con l'ordine generato dall'insieme. È necessario dimostrarlo: lasciamo una coppia arbitraria da, quindi, da allora ci sono sequenze e tali che, ad es. numero e

impostare il numero. Pertanto è un ordine contenente un insieme, ma

l'ordine minimo contenente mezzi.

Lasciamo, cioè è un numero ed è un numero impostato. Significa che

, . (3) Mostriamo che una coppia. Poiché, allora. Pertanto, secondo 1) . () Considerando che

Otteniamo Quindi, secondo 2), . ()Da ) e ) seguirà quello. E così via, continuando questo processo, otteniamo. Oppure, tenendo conto di 3), cioè .Quindi, lo hanno dimostrato.

Il teorema è stato dimostrato.

Teorema 2. Affinché un insieme finito di coppie sia un insieme generatore di un certo ordine, è necessario e sufficiente che sia antisimmetrico.

Dim. Se un insieme di coppie è antisimmetrico, allora per il Teorema 1 sarà un insieme generatore di ordine. Mostriamo il contrario. Lascia molte coppie

crea ordine. Mostriamo che è antisimmetrico. Lo dimostreremo per contraddizione. Supponiamo che non sia antisimmetrico, cioè c'è una serie di numeri

da un insieme che non sono contemporaneamente uguali a zero, tale che. È facile vedere che se una coppia appartiene a qualche relazione d'ordine, allora le coppie devono appartenere ad essa, e, quindi, anche la coppia deve appartenere ad essa. Allo stesso modo, qualsiasi coppia apparterrà a questo ordine.In base a questa osservazione, coppie

appartengono all'ordine. Poi.

Se un ordine contiene coppie, allora contiene coppie, . Pertanto, contiene una coppia. Applicando questo fatto all'ordine, possiamo scrivere. Pertanto,

Abbiamo scoperto che l'ordine contiene contemporaneamente coppie

e. E questo contraddice ciò che è una relazione d'ordine. La contraddizione risultante dimostra il teorema.

3. Ordini generati da un insieme di coppie coprime

In alcuni casi, a seconda della scelta del gruppo elettrogeno, la costruzione dell'ordine considerato nella sezione precedente viene notevolmente semplificata e diventa più intuitiva. Consideriamo uno di questi casi.

Definizione L'insieme delle coppie tale che, dove, è detto insieme delle coppie coprime.

Teorema 3. Sia dato un insieme di coppie coprime e indichiamo dove. Quindi e sono rappresentati nella forma Relazione binaria

Dov'è un ordine parziale.

Dimostrazione Per dimostrare il teorema è necessario dimostrare la riflessività, transitività, antisimmetria e stabilità della relazione binaria specificata. 1. La condizione è soddisfatta, perché ce ne sono. La riflessività è dimostrata.2. Lascia stare. Dalla condizione consegue che, e dalla condizione consegue che, quindi

Per certezza, assumeremo che tutto e tutti. Poi potrai scriverlo da qui

Esprimendo e, otteniamo, Sostituendo i valori

e nelle uguaglianze originali, troviamo che,. Pertanto,

e la transitività è dimostrata. Nel caso in cui alcuni

usiamo il fatto che, e la dimostrazione sarà simile.3. Lascia e. Mostriamolo. Dalle condizioni che,.Dalla condizione che segue che,.Chiudiamo transitivamente queste coppie, otteniamo, e da quanto dimostrato sopra.Ma poiché,.Di conseguenza, l'antisimmetria è dimostrata.4. La stabilità è evidente. Il teorema è stato dimostrato.

Teorema 4. Affinché un ordine possa essere generato da un insieme di coppie coprime, è necessario e sufficiente che sia quello descritto nel Teorema 3.

Prova. Indichiamo l'ordine generato dall'insieme delle coppie coprime e dobbiamo dimostrarlo.

1. -minimo

2. Allora

Mostriamo a cosa appartiene questa coppia. Per fare ciò è sufficiente dimostrarlo a partire dal fatto che

segue quello

appartiene, quindi,. Ne consegue che. Pertanto, l'inclusione viene eseguita per. Lascia che l'inclusione venga eseguita per, ad es. .Allora.Dal momento che.Di conseguenza, cioè. questa inclusione vale e le coppie appartengono.

Quindi, ricevuto e, quindi,

e il teorema è dimostrato.

È facile vedere che l'ordine generato da una coppia arbitraria è un caso speciale dell'ordine generato da un insieme di coppie coprime.

4. Ordini stabili sul semigruppo additivo dei numeri naturali, loro connessione con ordini sul semigruppo moltiplicativo dei numeri naturali.

Considera l'ordine sul semigruppo dei numeri naturali per addizione.

Una coppia arbitraria di numeri naturali può essere rappresentata come, o, o, dove. Consideriamo un insieme arbitrario di coppie rappresentabili nella forma

e disporli in ordine crescente. Indichiamo un tale insieme, cioè, ,

Teorema5. Affinché un ordine possa essere generato da un insieme di coppie è necessario e sufficiente che si tratti di una relazione binaria

Prova. Dimostriamo che una relazione binaria è una relazione d'ordine. Per fare questo dobbiamo mostrare quattro proprietà: 1. La riflessività segue dalla definizione 2. Dimostriamo la transitività. Sia E. Ne consegue dalla condizione che

Ne consegue dalla condizione che

Da queste uguaglianze otteniamo

Quelli. e la transitività è dimostrata 3. Antisimmetria. Permettere

E. Allora valgono le uguaglianze (1) . (2) Sostituisci 1) in 2) e ottieni. E questo significa che. Ma

e quindi. Quindi, cioè .Così,

antisimmetrico.4. La stabilità è evidente.

Quindi,

Relazione d'ordine. Resta da mostrare a cosa serve il gruppo elettrogeno.

Denota

un ordine generato da un insieme di coppie. Proviamo che coincide con.1. Appartiene una coppia arbitraria dell'insieme. Allo stesso tempo, secondo la definizione

può essere scritto

Quelli. .Di conseguenza, una coppia arbitraria di from sarà contenuta in, why per contenere tutte le coppie di gruppi elettrogeni dell'ordine.Abbiamo ottenuto questo.2. Mostriamo il contrario. Lasciamo, cioè,

È necessario dimostrare che. Considerando le uguaglianze di cui sopra, facciamo il seguente ragionamento.

Da cosa ne consegue che allora le coppie appartengono. Da qui. Dal fatto che, ne consegue che, cioè. Facendo un ragionamento simile ai precedenti, otteniamo. Continuando questo processo, arriviamo al seguente risultato: cioè , che significa .

Otteniamo che, quindi,

Il teorema è dimostrato Allo stesso modo, il teorema può essere dimostrato per l'insieme delle coppie duali dell'insieme.

Teorema6. Affinché un insieme di coppie generi un ordine su un semigruppo additivo di numeri naturali, è necessario e sufficiente che si tratti di un insieme o di un suo insieme duale.

Prova. 1. Se un insieme ha uno dei tipi specificati, allora per il Teorema 5 genera un ordine.

2. Lascia che generi ordine. Dimostriamo che è così

impostato o duale ad esso. La dimostrazione verrà effettuata con il metodo inverso. Lascia che l'insieme contenga coppie. Quindi anche queste coppie appartengono all'ordine generato.,

Quindi

Utilizzando argomenti simili ai precedenti otteniamo: Contiene quindi entrambe le coppie

E, e questo è contrario a quell'ordine. Di conseguenza, non possono esserci coppie e allo stesso tempo, cioè. è un insieme o il suo duale.

Il teorema è stato dimostrato.

È facile vedere che gli ordini stabili sul semigruppo additivo dei numeri naturali sono stabili anche sul semigruppo moltiplicativo dei numeri naturali. Anzi, lasciamo

ordine stabile Dalle condizioni seguono le uguaglianze,

Quindi, moltiplicando entrambi i membri di ciascuna uguaglianza per un numero naturale arbitrario ed effettuando semplici trasformazioni, otteniamo,

Quindi, .

Pertanto, l'insieme di tutti gli ordini stabili sul semigruppo additivo dei numeri naturali è contenuto nell'insieme di tutti gli ordini stabili sul semigruppo moltiplicativo dei numeri naturali. Sorge la domanda sull'insieme generatore di questi ordini nel semigruppo

Consideriamo, ad esempio, l'ordine di una finestra generata da una coppia. Questo sarà l'ordine normale. Si noti che oltre ad esso e al suo doppio ordine

Altri ordini lineari su

NO. Il gruppo elettrogeno minimo di ordine in

ci sarà un insieme di coppie. Ciò deriva dal fatto che qualsiasi coppia contenuta nell'ordine può essere ottenuta dall'insieme specificato e, allo stesso tempo, nessuna di queste coppie può essere ottenuta dalle altre utilizzando una chiusura transitiva o stabile . Quindi, in ordine

ha un gruppo elettrogeno infinito. È facile vedere che tutti gli ordini generati da un insieme finito di coppie hanno on

gruppi elettrogeni infiniti.

5. Ordini generati da un insieme infinito di coppie

Teorema 7. Insieme infinito di coppie

crea ordine

su un po' di algebra

se e solo se uno qualsiasi dei suoi sottoinsiemi finiti

genera un certo ordine

su questa algebra. Questo è definito come segue:

se e solo se esiste un finito tale.

Prova. Lascia che crei ordine. Scegliamo un sottoinsieme finito arbitrario

imposta. Quindi l'ordine minimo

Mostriamo il contrario. Sia un sottoinsieme finito arbitrario

imposta

crea ordine. Consideriamo una relazione tale che.1. , Perché . Quindi riflessivamente.2. Permettere

e. Allora, così

e, in modo tale da considerare. Allora lo si può scrivere

E. Noi riceviamo. Perciò. Quindi, transitivamente.3. Lascia e. Quindi, così quello e così quello. Ma esiste quello, e otteniamo. Pertanto è antisimmetrico 4. Sia dunque tale. Pertanto, da dove. stabile.

Quindi, soddisfa le proprietà di riflessività, transitività, antisimmetria e stabilità. Significa,

relazione d'ordine Proviamo che esiste un ordine generato da un insieme infinito. Denota

ordine generato. È necessario dimostrare che.1. Una coppia arbitraria è contenuta in, perché , che, quindi, . Ma l'ordine minimo contiene, quindi.

2. Sia quindi una coppia arbitraria quella, ad es.

la coppia è contenuta nell'ordine minimo generato da ma, da dove e quindi. Significa, .

Abbiamo ottenuto due inclusioni e, quindi, ad es. il set sta generando per.

Si prova così che se ogni sottoinsieme finito di un insieme infinito genera un ordine, allora anche l'infinito stesso genera un ordine, che è l'ordine specificato.

Il teorema è stato dimostrato.

Dal teorema dimostrato seguono dei corollari.

Definizione. Un insieme infinito di coppie di numeri naturali si dice antisimmetrico se uno qualsiasi dei suoi sottoinsiemi finiti è antisimmetrico.

ha dato origine all'ordine

sul semigruppo moltiplicativo dei numeri naturali è necessario e sufficiente che sia antisimmetrico.

se e solo se esiste un insieme finito tale che, dove

è l'ordine generato dall'insieme antisimmetrico, descritto nel paragrafo 2.

Definizione. Un insieme infinito di coppie di numeri naturali è detto -insieme se uno qualsiasi dei suoi sottoinsiemi finiti è -a-insieme.

Conseguenza. A un numero infinito di coppie

ha dato origine all'ordine

su un semigruppo additivo di numeri naturali è necessario e sufficiente che sia un insieme -o un suo insieme duale. Inoltre, se e solo se esiste un insieme finito tale che, dov'è l'ordine generato dall'insieme descritto al paragrafo 4.

M.: Nauka, 1970, 393 p.2 Lyapin, E.S. Ordinamenti nel semigruppo delle trasformazioni / E.S. Lyapin //Atti del quarto congresso matematico pan-sindacale, Leningrado: Nauka.1964.V.2.S.1314.3. Krivenko, V.M. . Lyakhova //XIX Conferenza algebrica di tutta l'Unione: abstract delle comunicazioni. – Istituto di problemi applicati di meccanica e matematica dell’Accademia delle scienze della SSR ucraina – Lvov, 1987, cap.1.S.148.

Valido (vero) i numeri sono ben noti dal corso di matematica scolastica. Soffermiamoci brevemente sulle loro proprietà, che sono abbastanza facilmente percepibili da ognuno di noi. I numeri reali formano un insieme di elementi con le seguenti proprietà.

Ordina proprietà

Per due numeri qualsiasi %%a%% e %%b%% viene definita la relazione d'ordine, ovvero Due numeri reali qualsiasi %%a%% e %%b%% soddisfano una delle seguenti relazioni: %%a< b, a = b%% или %%a >B%%; mentre se %%a< b%% и %%b < c%%, то %%a < c%%.

Proprietà dell'operazione di addizione

somma e indicato con %%a + b%% che valgono le seguenti proprietà.

commutatività: %%a + b = b + a %%.
Associatività: %%a + (b + c) = (a + b) + c%% per qualsiasi numero %%a, b%% e %%c%%.
zero e indicato con %%0%% , che è %%a + 0 = a%% per qualsiasi numero %%a%%.
Per ogni numero %%a%% c'è un numero chiamato opposto%%a%% e indicato con %%-a%%, quindi %%a + (-a) = 0%%.
Se un< b%%, то %%a + c < b + c%% для любого числа %%c%%. Нуль единственен, и для каждого числа единственно противоположное ему число. Для любой пары чисел %%a%% и %%b%% число %%a + (-b) %% называют differenza numeri %%a%% e %%b%% e rappresentano %%a - b%%.

Proprietà dell'operazione di moltiplicazione

Per ogni coppia di numeri %%a%% e %%b%% esiste un singolo numero, chiamato loro lavoro e indicato con %%ab%% (o %%a \cdot b%%) che valgono le seguenti proprietà.

commutatività: %%ab = ba%%.
Associatività: %%a(bc) = (ab)c%% per qualsiasi numero %%a, b%% e %%c%%.
C'è un numero chiamato unità e indicato con %%1%%, il che significa che %%a \cdot 1 = a%% per qualsiasi numero %%a%%.
Per ogni numero diverso da zero %%a%%, esiste un numero chiamato inversione a quello indicato e indicato con %%1 / a%%, che significa %%a \cdot (1 / a) = 1%%.
Se %%a%% o %%b%%, o entrambi %%a%% e %%b%% sono zero, allora %%ab = 0%%.
Se un< b%% и %%c >0%% quindi %%ac< bc%%. Единица единственна, и для каждого ненулевого числа существует единственное обратное к нему. Для любой пары чисел %%a%% и %%b (b \neq 0)%% число %%a \cdot (1/b)%% называют privato dalla divisione di %%a%% per %%b%% e denotare %%a / b%%.

Proprietà distributiva

Per ogni tripla dei numeri %%a, b%% e %%c%%, l'uguaglianza %%(a + b)c = ac + bc%% è vera.

Proprietà di Archimede

Qualunque sia il numero %%a%%, esiste un numero intero %%n \in \mathbb(N)%% tale che %%n > a%%.

Riso. 1. Linea numerica

Prima di enunciare la seguente proprietà dei numeri reali ricordiamo che la retta è data quadro di riferimento, se su questa linea sono fissati due punti diversi (punti %%O%% e %%e%% in Fig. 1). Quello a sinistra (punto %%O%%) è chiamato origine e la lunghezza del segmento %%Oe%% imposta l'unità di scala. Viene chiamata una retta con un dato sistema di riferimento asse delle coordinate. Di solito è indicato con %%Ox%%. Il punto %%O%% divide l'asse delle coordinate in due parti: il semiasse positivo, dove si trova il punto %%e%% e il semiasse negativo.

Coordinata i punti %%M%% sull'asse %%Ox%% nome la lunghezza del segmento %%OM%%, preso con il segno %%+%%, se il punto %%M%% giace sul semiasse positivo, e con il segno %%-% % se il punto %%M%% giace sul semiasse negativo.

Ovviamente ogni punto %%M%% sull'asse %%Ox%% corrisponde ad un numero reale %%x%%, cioè alla sua coordinata. E viceversa, ogni numero reale sull'asse %%Ox%% corrisponde a un punto di cui questo numero reale è la sua coordinata. Qualora sia richiesto, assumeremo che tale corrispondenza sia stabilita tra i numeri reali ed i punti di una retta, e %%e = 1%%, %%O = 0%%.

Pertanto, la raccolta di tutti i numeri reali può essere considerata come linea numerica. A volte, al posto della linea numerica, viene utilizzato anche il termine "linea reale". L'identificazione dei numeri reali con i punti sulla retta numerica sarà estremamente utile in futuro, poiché funge da strumento ausiliario per la comprensione e motivazione per introdurre nuovi concetti.

Viene chiamato il sottoinsieme %%X%% dell'insieme dei numeri reali spacco, se insieme a due numeri qualsiasi %%x_1, x_2%% questo sottoinsieme contiene qualsiasi %%x%% tra di loro. Utilizzare i seguenti tipi di intervalli:

%%(a, b) = \(x: a< x < b\}%% - intervallo, O divario aperto;
%% = $x: a \leq x \leq b$%% - segmento, O divario chiuso(a volte usa il termine "segmento");

%%(a, b] = \(x: a< x \leq b\}%% и %% \supseteq %%, то отрезок %%%% называют nidificato nell'intervallo %%%%.

Proprietà di continuità

Per ogni sistema di segmenti annidati $$ \supseteq \supseteq \supseteq \ldots \supseteq \supseteq \ldots $$, esiste almeno un punto che appartiene a tutti i segmenti del sistema dato. Questa proprietà è anche chiamata principio dei segmenti annidati (principio di Cantor).

Dalle proprietà elencate dei numeri reali si può ricavare che 1 > 0, nonché le regole per le operazioni con frazioni razionali; regole dei segni nella moltiplicazione e divisione dei numeri reali; regole per trasformare le uguaglianze e le disuguaglianze; Proprietà del valore assoluto di un numero reale.

Valore assoluto

Valore assoluto(O modulo) %%|a|%% di qualsiasi numero reale %%a%% è un numero reale che soddisfa le seguenti condizioni: $$ |a| = \begin(cases) a, \text( if ) a \geq 0 \\ -a, \text( if ) a< 0 \end{cases} ~~~~~~~~~~(1) $$

Ne consegue che il valore assoluto di qualsiasi numero reale è non negativo %%(|a| \geq 0)%%, e anche $$ \begin(array)(l) |a| = |-a|, \\ |a| \geq a, \\ |a| \geq -a, \\ -|a| \leq a \leq |a|. \end(array)~~~~~~~~~~(2) $$

Geometricamente, %%|a|%% corrisponde alla distanza tra i punti della linea numerica che rappresentano i numeri %%0%% e %%a%%.

Sia la disuguaglianza %%|a|< \varepsilon%%, где %%\varepsilon%% - некоторое положительное число (%%\varepsilon >0%% . Allora questa disuguaglianza è equivalente alla doppia disuguaglianza $$ -\varepsilon< a < \varepsilon. $$ Равносильность рассмотренных неравенств будет сохранена, если строгие неравенства (%%<%%) заменить на нестрогие (%%\leq%%): %%|a| \leq \varepsilon%% равносильно %%-\varepsilon \leq a \leq \varepsilon%%.

Per qualsiasi numero reale %%a%% e %%b%% l'uguaglianza $$ |ab| = |a||b| ~~~~~~~~~~(3) $$ e valgono le seguenti disuguaglianze: $$ \begin(array)(lr) |a + b| \leq |a| + |b| &~~~~~~~~~~(4),\\ |a - b| \geq \big||a| - |b|\big|&~~~~~~~~~~(5). \end(array) $$

Utilizzando (1) e (2), dimostriamo la disuguaglianza (4): se %%a + b \geq 0%%, allora $$ |a + b| = a + b \leq |a| + |b| $$ e se %%a + b< 0%%, то $$ |a + b| = -(a + b) = (-a) + (-b) < |a| + |b| $$

Le proprietà di cui sopra descrivono completamente l'insieme di tutti i numeri reali.

L'insieme di tutti i numeri reali, così come l'insieme dei punti sulla retta numerica, è solitamente indicato con %%\mathbb R%%.

Set completo di numeri reali

rifornito(O esteso) l'insieme dei numeri reali è l'insieme formato da tutti i numeri reali %%x \in \mathbb R%% con l'aggiunta di due elementi, denotati %%+\infty%% ("più infinito") e %%-\ infty%% (meno infinito). Si presuppone che %%-\infty< +\infty%% и для всех чисел %%x \in \mathbb R%% справедливо %%-\infty < x < +\infty%%. Пополненное множество обозначают %%\overline{\mathbb R}%%. Ему соответствует esteso(O rifornito) linea numerica. Gli elementi %%-\infty%% e %%+\infty%% sono chiamati punti infiniti di tale linea.

Sottoinsiemi dell'insieme %%\mathbb R%% dei numeri reali

Insieme di numeri interi$$ \mathbb Z = $\ldots, -3, -2, -1, 0, 1, 2, 3, \ldots $ $$ è un sottoinsieme proprio dell'insieme %%\mathbb R%% (%%\mathbb Z \subset \mathbb R%%).
Insieme dei numeri naturali$$ \mathbb N = $1, 2, 3, \ldots $ $$ è un sottoinsieme proprio di %%\mathbb Z %% e %%\mathbb R%% %%(\mathbb N \ sottoinsieme \mathbb Z \sottoinsieme \mathbb R)%%.

L'insieme di tutti i numeri reali che può essere rappresentato come quoziente dell'intero %%m \in \mathbb Z%% diviso per il numero naturale %%n \in \mathbb N%% è chiamato insieme numeri razionali e denotano %%\mathbb Q%%, cioè $$ \mathbb Q = \sinistra$\frac(m)(n): m \in \mathbb Z, n \in \mathbb N\right$ $$

I rapporti %%\frac(m)(n)%% e %%\frac(m")(n")%% sono considerati uguali (rappresentano lo stesso numero razionale %%r \in \mathbb Q%%), se %%mn" = nm"%%. Pertanto, ogni numero razionale %%r = \frac(m)(n)%% può avere infinite immagini %%r = \frac(p m)(p n), p \in \mathbb N%%.

Ovviamente, %%\mathbb N \subset \mathbb Z \subset \mathbb Q \subset \mathbb R%%.

Lacune infinite

Sulla linea dei numeri aumentati si distinguono intervalli infiniti $$ (b, +\infty) = $x: x > b$, (-\infty, a) = \(x: x< a\} $$ и бесконечные полуинтервалы $$ = \{x: x \leq a\} $$ По аналогии с бесконечными интервалами множество всех точек на числовой прямой R обозначают часто %%(-\infty, +\infty)%% или просто %%(-\infty, \infty)%%.

Riso. 2. Intorno di un punto

Viene chiamato qualsiasi intervallo %%(a, b)%% contenente qualche punto %%x_0%%. quartiere questo punto e denotare %%\text(U)(x_0)%%, cioè %%\text(U)(x_0) = (a, b)%% if %%x_0 \in (a, b)%%. Il punto %%x_0%%, situato al centro del suo quartiere %%(a, b)%%, in questo caso si chiama centro del quartiere, e la distanza %%\varepsilon = \frac((b - a))(2)%% è il raggio del quartiere. Quindi l'insieme %%\(x: |x - x_0|< \varepsilon\}%% называют %%\varepsilon%%-окрестностъю точки %%x_0%% и обозначают %%\text{U}(x_0, \varepsilon)%% или %%\text{U}_\varepsilon(x_0)%% (рис. 2).

Sulla retta reale estesa, viene introdotto il concetto di intorno anche per i punti infiniti %%+\infty%% e %%-\infty%%, equiparando quindi questi punti a quelli finiti quando si considerano molte questioni. Sia %%M%% un numero positivo. Quindi %%\text(U)(+\infty) = $x \in \mathbb(R): x > M$%% e %%\text(U)(-\infty) = $x \ in \mathbb(R): x< -M\}%%, а для объединения бесконечных точек %%\text{U}(\infty) = \{x \in \mathbb{R}: |x| >M$%%. Chiaramente, per uno qualsiasi degli infiniti punti, l'intorno con il %%M%% più piccolo include l'intorno con il %%M%% più grande.

Ministero dell'Istruzione e della Scienza della Federazione Russa

Agenzia federale per l'istruzione

ISTITUTO MUNICIPALE DI NIZHNEKAMSK

Dipartimento di Informatica, Matematica e Naturalmente -

discipline scientifiche

Gruppo 561

ASTRATTO

nella disciplina "Algebra astratta"

Specialista del livello di istruzione

Argomento: insiemi ordinati

Responsabile ___________________ R.M. Munipov

Studente ___________________ A.V. Glazunov

Nizhnekamsk 2007

INTRODUZIONE………………………………………..3

1. Insiemi parzialmente ordinati………………5

2. Set completamente ordinati………..20

3. Gruppoidi parziali e loro proprietà…………..23

CONCLUSIONE…………………..35

RIFERIMENTI………………….36

introduzione

Attualmente l'algebra è intesa principalmente come una teoria generale delle operazioni e delle relazioni algebriche. È caratterizzato da una grande naturalezza interiore delle idee e dei compiti originali, dall'unità dei metodi e dall'ampia ampiezza dei concetti di base. La sua area è delineata in modo chiaro e chiaro. Eppure i confini esistenti della teoria non possono essere considerati stabiliti in modo fermo e definitivo. Sempre più spesso comincia ad emergere il desiderio di andare oltre. Occorre considerare le operazioni non solo complete, ma anche parziali.

La teoria delle azioni parziali deve naturalmente continuare la teoria delle azioni complete. Quest'ultima è oggi estremamente ramificata, ricca e nel suo periodo di massimo splendore. Naturalmente nasce l'idea di trasferire i concetti ed i risultati lì sviluppati in un nuovo ambito. Ciò, ovviamente, è necessario e in molti casi fruttuoso. Tuttavia, già dai primi passi nello sviluppo della teoria delle azioni parziali, si fa sentire la significativa specificità di questa tendenza. Spesso il trasferimento diretto dei risultati della teoria delle azioni complete risulta difficile o addirittura impossibile. Il solito materiale algebrico deve essere sottoposto a un'elaborazione o un ripensamento significativo, inoltre sorgono nuovi concetti e compiti specifici per la nuova direzione. Richiedono una propria metodologia di ricerca.

Non c'è stata ancora un'esposizione sufficientemente completa e coerente della teoria delle azioni algebriche parziali. La discordanza prevale nei concetti iniziali e anche nella notazione e nella terminologia. Mancano collegamenti tra le singole opere. Si fa sentire l'insufficienza dell'elaborazione delle singole questioni necessarie alla costruzione di una teoria generale.

1 . Hinsiemi ordinati asticamente

Relazione binaria su un insieme UN chiamato antisimmetrico Se:

(AC UN) UN? V V? UN

UN chiamato riflettente Se:

( UN UN) UN UN

Relazione binaria su un insieme UN chiamato transitivo Se:

(UN,V,C UN) UN V V C>a Con

Esempio 1

Rapporto di divisibilità (intero) sull'insieme dei numeri naturali N antisimmetrico. Infatti, se UN V, V UN, poi ci sono naturali Q1 ,Q N, tale che un=bQ1 , b=aQ Dove un=unQ1 Q , questo è Q1 Q = 1. Ma,

Q1 ,Q N,quindi Q1 = Q = 1, da cui consegue che un = c.

Relazione binaria riflessiva transitiva antisimmetrica su un insieme UN chiamato relazione d'ordine (ordine parziale) sul set UN.

Un mucchio di UN con una relazione di ordine parziale data su di esso? chiamata insieme parzialmente ordinato e denotare< UN; ? >.

Nel seguito, per comodità, utilizzeremo l'abbreviazione AMICO , che denota un insieme parzialmente ordinato.

Esempio 2

< N, ? > ? la solita disuguaglianza non rigorosa dei numeri (nel senso scolastico). Necessità di dimostrare la transitività, la riflessività e l'antisimmetria di questa relazione?.

UN)UN? UN,(2 ? 2) - riflessività,

b) se UN? V , V? Con, Quello UN ? C, (3 ? 4, 4 ? 5 > 3 ? 5) - transitività,

c) se UN ? V , V?UN, Quello UN= dentro,(3 ? 3, 3 ? 3 > 3=3) - antisimmetria.

Ne consegue che < N, ? > - AMICO.

Esempio 3

< N, > .

a) Il rapporto di divisibilità sull'insieme dei numeri naturali N riflessivamente, perché ogni numero è multiplo di se stesso, cioè perché per chiunque UN N Sempre UN = UN 1 (1 N), questo, nel significato della relazione, abbiamo UN UN. Pertanto, di riflesso.

B) Se il primo numero è divisibile per il secondo (cioè multiplo del secondo), e il secondo è multiplo del terzo, allora il primo è multiplo del terzo, allora la relazione è transitiva, cioè Se UN V, V Con, UN,V,C N. Quindi ce ne sono Q ,Q N, Che cosa

UN= polliciQ ,

in =C Q ,

UN = C (Q Q ).

Denota: Q = Q Q N. Abbiamo

Dove Q N, cioè. UN Con- a priori . Pertanto la relazione è transitiva.

c) L'antisimmetria della relazione deriva dal fatto che due numeri naturali multipli tra loro sono uguali tra loro, cioè Se UN V, V UN, allora esistono Q1 ,Q N, Che cosa

un=bQ1 ,

b=aQ ,

un=unQ1 Q ,

questo è Q1 Q = 1. Ma, Q1 ,Q N,quindi Q1 = Q = 1, da cui consegue che un = c. Quindi è antisimmetrico.

Esiste quindi un ordine parziale e quindi < N, > - CHUM (insieme parzialmente ordinato).

Elementi UN,V Appestare UN chiamato incomparabile sono scritti

UN|| V, Se UN? V E V? UN.

Elementi UN,V Appestare UN chiamato paragonabile Se UN? V O V? UN.

Ordine parziale? SU UN chiamato lineare, ma l'amico stesso linearmente - ordinato O catena se ci sono due elementi da UN sono comparabili, cioè per ogni UN,V UN, O UN ? V, O V? UN.

Esempio 4 .

< N, ? >, < R, ? > - sono una catena. Tuttavia<В(M) ; > , dove B( M) - l'insieme di tutti i sottoinsiemi dell'insieme M o in( M) è chiamato booleano sul set M, non è una catena, perché non per due sottoinsiemi qualsiasi M uno è un sottoinsieme dell'altro.

Permettere < UN, ? > - CHUM arbitrario.

Elemento M UN chiamato mini piccolo, se per qualsiasi X UN da cosa X ? M Dovrebbe X = M.

Il significato di questo concetto è quello UN non contiene elementi strettamente inferiori a questo elemento M. Dicono che X rigorosamente meno M e scrivi X< M, Se X ? M, ma inoltre X ? M. Allo stesso modo, viene determinato l'elemento massimo di questo PLB. È chiaro che se M , M - diversi elementi minimi (massimi) del PLAT, quindi M || M .

Nella teoria degli insiemi parzialmente ordinati, la condizione UN ? V a volte leggi così: elementoUN contenuto nell'elementoV O elementoV contiene l'elementoUN .

Lemma.

Ogni elemento di una Piaga finita contiene un elemento minimo ed è contenuto nell'elemento massimo di questa Piaga.

Prova:

Permettere UN- elemento arbitrario della Piaga finale S. Se UN - elemento minimo, quindi, per effetto della riflessività, il lemma è dimostrato. Se UN non è minimo, allora c'è un elemento UN tale che

UN < UN(1)

Se UN è minimo, allora tutto è dimostrato. Se l'elemento UN non è

minimo, quindi per alcuni UN noi abbiamo

UN < а (2)

Se UN è minimo, allora da (1), (2), a causa della transitività, concludiamo che UN contiene l'elemento minimo UN . Se UN non è minimo, quindi

UN < UN (3)

per alcuni UN S. E così via. Questo processo non può essere infinito data la finitezza dell'insieme stesso S.

Quindi, su alcuni N-esimo passo del ragionamento, il processo viene interrotto, il che equivale al fatto che l'elemento UN minimo. In cui

UN < а < < а < а < а

Per transitività ne consegue che l'elemento UN contiene l'elemento minimo UN . Allo stesso modo, l'elemento UN contenuto nell'elemento massimo. Il lemma è dimostrato.

Conseguenza.

Il PLB finale contiene almeno un elemento minimo.

Ora introduciamo la nozione, importante per un’ulteriore esposizione, grafici piaga finale S.

Per prima cosa prendiamo tutti gli elementi minimi M , M , M V S. Secondo l'indagine ci sono. Quindi in un insieme parzialmente ordinato

S = S \ {M , M , M },

che, come S, è finito, prendiamo gli elementi minimi,

, , e consideriamo l'insieme

= S \ {, , }

Elementi della “prima riga” M , M , M rappresentato da punti. Un po' più in alto contrassegniamo gli elementi della “seconda fila” con punti, , e collega i punti con segmenti se e solo se M <

Successivamente troviamo gli elementi minimi della Peste, li rappresentiamo come punti della “terza fila” e li colleghiamo con i punti della “seconda fila” nel modo sopra indicato. Continuiamo il processo finché tutti gli elementi di questa Piaga non saranno esauriti S. Il processo è finito a causa della finitezza dell'insieme S. Viene chiamato l'insieme risultante di punti e segmenti diagramma Peste S. Allo stesso tempo UN < в se e solo se dal “punto” UN puoi andare su "punti" V lungo una linea spezzata “ascendente”. A causa di questa circostanza, qualsiasi PLB finito può essere identificato con il suo diagramma.

Esempio 5 .

Eccolo dato dal grafico S = {M , M , , ), in cui M < , M < , M < M < , M < M < , M < .

Elemento M chiamato meno elemento della Peste, se del caso X UN Sempre M ? X.

È chiaro che l'elemento più piccolo è minimo, ma non è vero il contrario: non tutti gli elementi minimi sono il più piccolo. L'elemento più piccolo (se presente) è solo uno. L'elemento più grande è definito in modo simile.

Esempio 6.

· · · ·

Questo è un PLB i cui elementi sono incomparabili a coppie. Tale parzialmente

vengono chiamati gli insiemi ordinati anticatene.

Esempio 7 .

Questa catena è con l'elemento più piccolo e quello più grande. Dove 0 è l'elemento più piccolo e 1 è l'elemento più grande.

Permettere M- un sottoinsieme di un insieme parziale ordinato UN. Elemento UN UN chiamato faccia inferiore imposta M, Se UN? X per chiunque X M.

Il più grande di tutti i limiti inferiori dell'insieme M, se esiste, viene chiamato bordo inferiore esatto imposta M e denotare inf M.

Permettere < UN, ? > - CHUM arbitrario. Elemento Con UN chiamato bordo inferiore esatto elementi UN,V UN, Se Con= inf( UN,V}.

Osservazione 1.

Non tutti i PLB hanno un limite inferiore esatto per due elementi qualsiasi.

Mostriamolo con un esempio.

Esempio 8 .

Per ( UN;C},{D;e) non ha limite inferiore,

inf( UN;V}=D, inf( V;C}=e.

Esempio 9 .

Diamo un esempio di un PLB che ha un minimo per qualsiasi elemento.

inf( UN;V}=D, inf( UN;D}=D, inf( UN;0 }=0 , inf( UN;C}=0 , inf( UN;e}=0 ,

inf( V;C}=e, inf( V;e}=e, inf( V;D}=D,

inf( C;e}=C, inf( C;0 }=0 , inf( C;D}=0 ,

inf( D;e}=0 , inf( D;0 }=0 ,

inf( e;0 }=0 .

Definizione: Si dice un insieme parzialmente ordinato in cui per due elementi qualsiasi esiste un minimo semi-reticolo.

Esempio 10 .

Facciamo un esempio di poset che non sia un semireticolo.

Permettere < N, ? > è un insieme ordinato linearmente di numeri naturali e e , e N. Sul set N = N { e , e ) definire una relazione binaria? , supponendo che X ? sì, Se X, sì N, Dove X ? sì, o se X N, sì { e , e ). Consideriamo inoltre per definizione: e ? e , e ? e .

Lo schema di questa PIATTAFORMA è il seguente:

Qualsiasi numero naturale n ? e e n? e , ma in N non esiste un elemento più grande, quindi, N - Amico, ma non un mezzo reticolo.

Quindi, per definizione, un semireticolo è un modello (come un insieme con una relazione?). Come vedremo ora, è possibile un altro approccio al concetto di semireticolo, ovvero un semireticolo può essere definito come una certa algebra.

Per fare ciò introduciamo alcune nozioni algebriche aggiuntive. Come è noto, semigruppoè un insieme non vuoto su cui è definita un'operazione algebrica binaria associativa.

Di solito viene indicato un semigruppo arbitrario S(semigruppo).

Definizione. Elemento eS chiamato idempotente, Se

e = e, questo è e · e = e.

Esempio 11 .

Semigruppo< N; · > ? ha l'unico idempotente 1.

Semigruppo< Z; + > ? ha l'unico idempotente 0.

Semigruppo< N; + > ? non ha un idempotente, perché 0 N.

Per ogni insieme X non vuoto, come al solito, l'insieme di tutti i sottoinsiemi dell'insieme X è denotato dal booleano dell'insieme X.

Semigruppo<В;>- è tale che ciascuno dei suoi elementi è idempotente.

UN IN, UN = UN UN.

Viene chiamato il semigruppo semigruppo idempotente O fascio se ciascuno dei suoi elementi è idempotente. Pertanto, qualsiasi valore booleano rispetto all'unione è un esempio di connettivo.

Esempio 12 .

Permettere X- un insieme arbitrario.

B è l'insieme di tutti i sottoinsiemi dell'insieme X.

B- è chiamato booleano sul set X.

Se X= (1,2,3) , quindi

B = (O,(1),(2),(3),(1,2),(2,3),(1,3),(1,2,3)).

Dall'intersezione di due sottoinsiemi dell'insieme Xè ancora una volta un sottoinsieme in X, allora abbiamo un gruppoide< В;>, inoltre, è un semigruppo e anche un fascio, poiché UN In e UN = UN UN=UN.

Allo stesso modo, abbiamo una connessione<; В > .

Si chiama la connessione commutativa semireticolo.

Esempio 13 .

Permettere X= (1,2,3), costruisci un diagramma< В ; >.

Facciamo esempi di PLAT, ma non di semireticolo.

Esempio 14 .

Amico con due facce inferiori e E D , che non sono paragonabili tra loro: e|| D. Pertanto, inf( UN;Con) non esiste.

Esempio 15.

Amico con due facce inferiori Con E D, che non sono paragonabili tra loro: Con|| D. Pertanto, inf( UN;V) non esiste.

Diamo esempi di semireticoli.

Esempio 16 .

Diagramma:

inf( UN;V}=V, inf( UN;Con}=Con, inf( UN;D}=D,

inf( V;C}=D, inf( V;D}=D,

inf( C;D}=D.

Esempio 17 .

È un semireticolo, perché per due elementi qualsiasi c'è un minimo, cioè

inf( UN;V}=V, inf( UN;Con}=Con, inf( V;C}=Con.

Teorema 1.

Permettere<S ; ? > - semireticolo. Poi<S ; > connessione commutativa, dove

UN V= inf ( UN,V} (*).

Prova:

È necessario dimostrarlo<S ; > valgono le seguenti identità:

(1) X y=y X

(2) (X sì) z=x (sì z)

(3) X X = X

1) Secondo l'uguaglianza(*)

X y= inf( X,sì) = inf( sì,X) = sì X

2) Denotare UN = (X sì) z, in =X ( sì z)

Dimostriamolo UN = V.

Per questo è sufficiente dimostrarlo

UN ? V (4)

V ? UN(5) (a causa dell'antisimmetria)

Denota

Con = X sì , D = sì z

Ai sensi di, UN limite inferiore esatto tra Con E z

UN? Con , UN ? z , C ? X, Pertanto, a causa della transitività UN ? X.

Allo stesso modo, UN? sì, cioè. UNè il limite inferiore comune per sì E z. UN Dè il loro minimo.

Quindi, UN ? D, Ma V= inf( X, D}.

Dalla disuguaglianza UN ? X , UN ? D segue quello UN X E D, UN Vè il loro minimo, quindi,

UN? V(4) dimostrato.

(5) si dimostra in modo simile.

Da (4) e (5), vista l'antisimmetria, concludiamo che

a = pollici.

Con ciò abbiamo dimostrato l'associatività dell'operazione ().

3) Abbiamo X X= inf ( X,X} = X.

L’uguaglianza è soddisfatta dalla riflessività: X? X.

Quello. algebra costruita<S ; > sarà un semigruppo commutativo idempotente, cioè legame commutativo.

Teorema 2.

Permettere<S ; · > è un semigruppo idempotente commutativo, quindi una relazione binaria? SU S, uguaglianza definita

? = UNv = a,

è un ordine parziale. Allo stesso tempo, il<S ; ? > è un semireticolo.

Prova:

1) riflessività?.

Per condizione<S ; > soddisfa tre identità:

(1) X = X

(2)x y = yx

(3) (xy)· z = x(sì· z)

Poi xx = x =x- a causa di (1). Ecco perché X? X.

2) antisimmetria? .

Permettere X? A E A? X, quindi per definizione,

(4) xy = x

quindi, a causa della commutatività, abbiamo x = y.

3) transitività?.

Permettere X? A E A?z quindi, per definizione,

(6) xy = x

(7) sì z= sì

Abbiamo X· z = (X· sì)· z X· (sì· z) xy X

COSÌ, X· z = X, questo è X?z.

Quindi, abbiamo un CHUM<S ; ? >. Resta da dimostrare che per ogni ( UN,V)S esiste inf( AC}.

Prendiamo arbitrario UN,V S e dimostrare che l'elemento c = un bè inf( AC), cioè. Con= inf( AC}.

Infatti,

c un =(AC)·UN UN·(AC) (aa)· V un b = c,

Quello. Con? UN.

Allo stesso modo, s h =(AC)·V UN·(dentro dentro) un b = c,

quelli. Con? V.

COSÌ, Con- comune inferiore ( AC}.

Dimostriamo la sua accuratezza.

Permettere Dè un limite inferiore comune per UN E V:

(8) D? UN

(9) d? V

(10) d un = d

(11) d in =D

D· C = D· (AC) (D·UN)· V D·V D,

D· C = D, quindi, D ? C.

Conclusione: c = inf( UN,V}.

I Teoremi 1 e 2 dimostrati ci permettono di guardare ai semireticoli da due punti di vista: come poset e come algebra (semigruppi commutativi idempotenti).

2. Insiemi ben ordinati

La teoria degli insiemi ordinati è stata formulata da G. Cantore . Shatunovsky . Hausdorff (1914).

Insiemi ben ordinati Un insieme ordinato si dice ben ordinato se ciascuno dei suoi sottoinsiemi ha un primo elemento (cioè un elemento seguito da tutti gli altri). Tutti gli insiemi ordinati finiti sono ben ordinati. Una serie naturale ordinata in ordine crescente (così come in altri modi) forma un insieme ben ordinato. L'importanza degli insiemi ben ordinati è determinata principalmente dal fatto che per essi vale il principio di induzione transfinita.

Gli insiemi ordinati che hanno lo stesso tipo di ordine hanno anche la stessa cardinalità, quindi possiamo parlare della cardinalità del tipo di ordine dato. D'altra parte, insiemi ordinati finiti della stessa cardinalità hanno lo stesso tipo di ordine, quindi ciascuna cardinalità finita corrisponde a un certo tipo di ordine finito. La situazione cambia passando agli insiemi infiniti. Due insiemi ordinati infiniti possono avere la stessa cardinalità ma tipi di ordine diversi.

3. Gruppoidi parziali e loro proprietà

Come è noto, un'operazione algebrica binaria su un insieme Sè una mappatura da un quadrato cartesiano S?S. In questo caso diciamo che un'azione è data S. Lo chiameremo in questa sezione azione completa.

Qualsiasi mappatura da un sottoinsieme S?S V S chiamato azione parziale SU S. In altre parole, un effetto parziale su Sè una funzione da S?S > S.

Si può dire così S viene data un'azione parziale (moltiplicazione parziale) se per qualsiasi elemento AC S lavoro AC o non definito o definito in modo univoco. In poche parole, non tutti gli elementi vengono moltiplicati qui.

Un mucchio di S con la moltiplicazione parziale data in esso si chiama gruppoide parziale e indicato ( S ; · ) in contrasto con il gruppoide completo< S ; · >.

Se per un gruppoide completo possiamo parlare della tabella Cayley, allora per un gruppoide parziale possiamo parlare di un analogo della tabella Cayley, vale a dire una tabella del genere quando alcune celle sono vuote - questo è quando il prodotto degli elementi è indefinito.

Esempio 1


	UN

UN· dentro = dentro, Ma V· UN non definito, cioè V· UN= O. Simbolo " O" non appartenere S, cioè. non è un elemento da S.

Esempio 2

Consideriamo la CUM ( S ; ? ).

S = {UN,V,C, D), Dove UN? UN, V? V, Con? Con, D ? D, Con? UN, Con? V, D? UN, D? V.

In una piaga arbitraria ( S ; ? ) indicheremo:

UN V= inf( UN,V}.

Quindi il POI fornito nell'esempio rispetto a questa azione parziale è un gruppoide parziale ( S;), il cui tableau di Cayley è il seguente

			D
UN
			D
	C
		-

In questa sezione considereremo tre tipi di associatività: associatività forte, associatività media e associatività debole.

Definizione 1.

Gruppoide parziale ( S ; · ) è chiamato debolmente associativo , Se

(X,y,z S) (X· sì)· z O X·( sì· z) > (X· sì)· z= X·( sì· z) (*)

Definizione 2.

Gruppoide parziale ( S ; · ) è chiamato associativo medio , Se

(X,y,z S) (X· sì)· z O sì· z > (X· sì)· z= X·( sì· z)

Definizione 3.

Gruppoide parziale ( S ; · ) è chiamato fortemente associativo , Se

(X,y,z S) [(X· sì)· z O X·( sì· z) O> (X· sì)· z= X·( sì· z)] (*)

Un gruppoide parziale fortemente associativo soddisfa le proprietà di associatività media e debole. Tuttavia, il contrario non è affatto necessario.

Esempio 3

Dato UN = {UN,in,s). Chiediamo UN moltiplicazione dell'azione parziale per “tabella Cayley parziale”.

Otteniamo un gruppoide parziale. Controlliamo se il group-poid sarà fortemente associativo.

Permettere ( X· sì)· z O Perché X UN, allora neanche x = c x = pollici

1) lascia x = c, Poi y = pollici y = c

a) lascia y = pollici, Poi z = UN

(Con· V)· UN O Con·( V· UN) definito

(Con· V)· un = c·( V· UN) vale l'uguaglianza

b) lascia y = c, Poi z= pollici z= con

e se z= pollici, Poi

(Con· Con)· V O Con·( Con· V) definito

(Con· Con)· in = con·( Con· V) vale l'uguaglianza

b") se z= con, Poi

(Con· Con)· Con O Con·( Con· Con) definito

(Con· Con)· c = c·( Con· Con) vale l'uguaglianza

2) lascia x = pollici, Poi y = a, UN z= pollici z = C

e se y = a E z= pollici

(V· UN)· V O= pollici·( UN· V) non definito

(V· UN)· V V·( UN· V) l'uguaglianza non è soddisfatta

b) lascia y = a E z= con

(V· UN)· Con O= pollici·( UN· Con) non definito

(V· UN)· Con V·( UN· Con) l'uguaglianza non è soddisfatta

Quindi, per definizione, un gruppoide parziale non è fortemente associativo. Ma questo ancora non significa questo S ; · ) non è debolmente associativo.

Scopriamolo.

Permettere (X· sì)· z O X·( sì· z) O .

A X UN, A UN, ovvero quando

x = pollici x = c

y = pollici y = c

questo gruppoide parziale è debolmente associativo.

Esempio 4

Permettere A ={UN, dentro, con), può essere impostato su UN la seguente tabella di Cayley. Otteniamo un gruppoide parziale. Controlliamo se questo gruppoide è mediamente associativo.

Permettere ( X· sì)· z O Perché X V, Poi x = a x = c

1) lascia x = a, Poi y = a y = pollici

a) lascia y = a, Poi z = UN, z= pollici

e se z= un, Poi

(UN· UN)· UN O UN· UN definito

(UN· UN)· UN UN·( UN· UN) l'uguaglianza non è soddisfatta

b") se z= pollici, Poi

(UN· UN)· V O UN· V definito

(UN· UN)· V UN·( UN· V) l'uguaglianza non è soddisfatta

Da qui vediamo che il gruppoide non è mediamente associativo. Scopri se è debolmente associativo.

Permettere ( X· sì)· z O X·( sì· z) O, Perché X V, Poi x = a x = c

1) lascia x = a, Poi y = a y = pollici

a) lascia y = a, Poi z = UN, z= pollici

e se z= un, Poi

(UN· UN)· UN O= un·( UN· UN) non definito

(UN· UN)· UN UN·( UN· UN)

b") se z= pollici, Poi

(UN· UN)· V O UN·( UN· V) definito

(UN· UN)· c = a·( UN· V) vale l'uguaglianza

b) lascia y = pollici, Poi z = UN, z= pollici

e se z= un, Poi

(UN· V)· UN O= un·( V· UN) non definito

(UN· V)· UN UN·( V· UN)

b") se z= pollici, Poi

(UN· V)· V O UN·( V· V) non definito

(UN· V)· V UN·( V· V) l'uguaglianza non è soddisfatta

2) lascia x = c, Poi y = a,y = pollici

a) lascia y = a, Poi z = UN, z= pollici

e se z= un, Poi

(Con· UN)· UN O= con·( UN· UN) non definito

(Con· UN)· UN Con·( UN· UN) l'uguaglianza non è soddisfatta

b") se z= pollici, Poi

(Con· UN)· V O Con·( UN· V) definito

(Con· UN)· in = con·( UN· V) vale l'uguaglianza

Quindi vediamo che il gruppoide parziale è debolmente associativo quando x = a E z= pollici o quando x = c Se y = a E z= pollici.

Definizione 4.

Gruppoide parziale ( S ; · ) è chiamato commutativo , Se

(X,sì S) X· sì = sì· X

Definizione 5.

Gruppoide parziale ( S ; · ) è chiamato catenaria , Se

(X,y,z S) (X· sì O sì· z) > [(X· sì)· z O X·( sì· z)]

Definizione 6.

Gruppoide parziale ( S ; · ) è chiamato idempotente , Se

(X S) X = X

Facciamo un esempio di gruppoide parziale non catenario.

Esempio 5

			D
UN
			D
	C
		-

Abbiamo Con un = c O, UN D = D O. Tuttavia, ( Con UN) D = C D O. Pertanto, il CG indicato non è catenaria.

È chiaro che con il termine intendiamo “limite superiore comune” degli elementi UN E V qualche amico.

Definizione 7.

Si chiama la peste categorico , se due qualsiasi dei suoi elementi che hanno un limite superiore hanno un limite inferiore esatto.

Esempio 6

Esempio 7

Insieme parzialmente ordinato definito dal tableau di Cayley:

Esempio 8

insieme parzialmente ordinato

avendo la seguente tabella Cayley:


				-
				-
				-

È chiaro che qualsiasi semireticolo è un PLAT categorico (ma non viceversa), perché due elementi qualsiasi hanno un limite inferiore esatto. In altre parole, la classe di tutti i poset categoriali contiene la classe di tutti i semireticoli, ma non coincide con essa. Quello. ogni proposizione dimostrata per poset categoriali comporta, come ovvia conseguenza, qualche teorema sui semireticoli.

Diamo esempi di semireticoli.

Esempio 9

Diagramma:

chiamato diamante

			D
UN
		D
	C

Esempio 10

Diagramma:

chiamato Pentagono, ed è determinato da un semireticolo avente la seguente tabella di Cayley:

Esempio 11.

Il semireticolo dato dalla tabella Cayley:

ha uno schema:

Teorema 1.

Permettere ( S ; ? ) è un PLAT categorico, allora ( S;) è un gruppoide parziale commutativo debolmente associativo della catenaria.

Prova:

Per chiunque UN S Sempre

UN UN= inf( UN, UN} = UN quindi il gruppoide parziale S idempotente.

Abbiamo UN V= inf( UN,V) = inf( V,UN} = V UN, e quindi S commutativo.

Controlliamo l'associatività debole.

Permettere ( UN V) Con O UN (V Con) , denota

UN V = D, V Con = e, (UN V) Con= D Con = F, UN (V Con) = UN e= G

Dimostriamolo F = G.

Per definizione, abbiamo F ? D ? UN F ? UN,

F ? D? V F? V (1)

F ? C (2)

Perché e= inf( dentro, con), allora da (1), (2) segue che F ? e. Quello. F - qualche limite inferiore comune per UN E e, UN G è il loro massimo minimo, quindi

F ? G (3)

Allo stesso modo,

G ? F (4)

Disuguaglianza (3), (4) e antisimmetria della relazione? fornire F = G. Si dimostra una debole associatività.

Controlliamo la catenarità S.

Permettere UN V O V Con, denota UN dentro = x, V Con = sì, quindi X? V, A? V, cioè.

V- limite superiore comune X E A. Perché AMICO S categoricamente, allora esiste inf( x,y), cioè. esiste in S X A. Denota X y= z, lo mostreremo

UN (V Con) = X Con= z. Abbiamo z ? X, z ? sì (Perché z = inf( x,y}), sì ? z z ? X, z ? C,

z - limite inferiore per X E Con.

Forniamo precisione.

Permettere T ? X , T ? C (T- qualsiasi limite inferiore), perché T ? X , Quello T ? UN, T? V, per condizione T? Con, cioè. Tè il limite inferiore comune per V E Con. Da ciò segue, per definizione, A, T ? sì.

COSÌ, T ? X, T? A quindi T ? z (a-prior z).

catenaria è stata dimostrata.

Teorema 2.

Se ( S ; · ) è un gruppoide parziale catenaria idempotente commutativa debolmente associativa, quindi la relazione

? = (AC) S?S (2)

È una relazione d'ordine. Allo stesso tempo, il<S ; ? > - è una catenaria.

Prova:

Dimostriamo la riflessività della relazione? . Perché gruppoide parziale S Idem-tenten, quindi UN· UN = UN quindi, per definizione (2) UN? UN.

Controlliamo l'antisimmetria.

Se UN? dentro, dentro? UN, Quello un b = un, b un = c, le parti di sinistra sono uguali in vista della commutatività, il che significa che le parti di destra sono quindi uguali a = pollici.

Resta da dimostrare la transitività.

Permettere UN? V, V? Con, Poi un b = un, vs = pollici, uns =(AC)· Con. Per catenarità abbiamo ( UN· V)· Con O , UN·( V· Con) O, quindi a causa della debole associatività

(AC)c = a(contro s), e quindi un c = un(contro s) = un b = un.

COSÌ, un c = un, cioè. UN? Con.

Quello. abbiamo un amico<S ; ? > .

Permettere z- limite superiore comune per X E A. Quindi, X?z, sì ? z, quindi X·z = X, sì· z = sì, Poi z· sì = sì. A causa della catenarità ( X· sì)· z O X· sì O.

Denota xy =S, lo dimostriamo S limite inferiore esatto.

Abbiamo S· X = (X· sì)· X = X· (X· sì) = (X· X)· sì = X· sì = S (in considerazione della catenarità e della debole associatività), quindi, S ? X, cioè. Sè il limite inferiore comune.

Da questi teoremi discendono due corollari noti nella teoria dei semireticoli.

Conseguenza 1.

Se<S ; · > è un semigruppo commutativo idempotente, allora la relazione? , definito dall'uguaglianza (2), è un ordine parziale. Tuttavia, per due elementi qualsiasi in S esiste un limite inferiore esatto.

Conseguenza 2.

Se<S ; · > è un insieme parzialmente ordinato in cui due elementi qualsiasi hanno un minimo, quindi rispetto all'operazione

UN V= inf( UN,V} (3)

un mucchio di Sè un semigruppo commutativo idempotente.

CONCLUSIONE

In conclusione, si può notare che la teoria degli insiemi ordinati è stata creata da G. Cantore . Nel 1883 introdusse il concetto di insieme ben ordinato e di numero ordinale, e nel 1895 il concetto di insieme ordinato e di tipo ordinale. Nel 1906-07 S.O. Shatunovsky formulò le definizioni di un insieme diretto (per Shatunovsky - un complesso localizzato) e di un limite su un insieme diretto (dai matematici americani E . G. Moore e G. L. Smith, questi stessi concetti furono considerati indipendentemente da Shatunovsky, ma molto più tardi - nel 1922). Il concetto generale di insieme parzialmente ordinato appartiene a F. Hausdorff (1914).

Pertanto, la teoria delle azioni algebriche parziali, essendo una continuazione della teoria delle azioni complete, utilizzando i suoi risultati, collegati ad essa da idee ed esperienze di applicazioni al di fuori dell'algebra, dovrebbe tuttavia prendere forma come una direzione indipendente nel vasto campo della moderna algebra.

Ad oggi sono stati pubblicati centinaia di articoli specificatamente dedicati allo studio delle azioni parziali. Per quanto riguarda le opere in cui nel corso dello studio si verifica una o l'altra azione parziale, il loro numero non può essere stimato. Le azioni parziali vengono trattate anche in alcune opere di algebrica generale, ma sempre molto brevemente.

Bibliografia

A.K. Clifford, G. Preston. Teoria algebrica dei semigruppi. 1972.

Greitzer. Teoria generale dei reticoli Mosca.-284p.

Kozhevnikov O.B. Insiemi parzialmente ordinati di gruppoidi parziali. Mosca, 1998. - 680.

E.S. Lyapin. Semigruppi. Mosca: fisica e matematica, 1960.- 354p.

Lyapin E.S. Algebra e teoria dei numeri. Mosca, 1980.-589p.

Come sai, l'insieme dei numeri naturali può essere ordinato utilizzando la relazione "minore di". Ma le regole per costruire una teoria assiomatica richiedono che questa relazione non sia solo definita, ma anche fatta sulla base di concetti già definiti nella teoria data. Questo può essere fatto definendo il rapporto "minore di" attraverso l'addizione.

Definizione. Il numero a è inferiore al numero b (a< b) тогда и только тогда, когда существует такое натуральное число с, что а + с = B.

In queste condizioni si dice anche che il numero B Di più UN e scrivi b > a.

Teorema 12. Per qualsiasi numero naturale UN E B Si verifica una ed una sola delle seguenti tre relazioni: a = b, a > b, UN < B.

Omettiamo la dimostrazione di questo teorema.. Da questo teorema segue che se

un¹b, O UN< b, O a > b quelli. la relazione "minore di" ha la proprietà della connessione.

Teorema 13. Se UN< b E B< с. Quello UN< с.

Prova. Questo teorema esprime la proprietà di transitività della relazione “minore di”.

Perché UN< b E B< с. quindi, per la definizione della relazione "minore di", esistono tali numeri naturali A E allora b = a + k e c = b + I. Ma allora c = (a+k)+ / e in base alla proprietà di associatività dell'addizione otteniamo: c = a+(k+/). Perché il k + io - numero naturale, quindi, secondo la definizione di "minore di", UN< с.

Teorema 14. Se UN< b, non è vero questo B< а. Prova. Questo teorema esprime la proprietà antisimmetria rapporto "meno".

Dimostriamolo prima per qualsiasi numero naturale UN non tu-!>! ■ )il suo atteggiamento UN< UN. Supponiamo il contrario, cioè Che cosa UN< а si verifica. Quindi, secondo la definizione della relazione "minore di", esiste un numero così naturale Con, Che cosa UN+ Con= UN, e questo contraddice il Teorema 6.

Dimostriamo ora che se UN< B, allora non è vero B < UN. Supponiamo il contrario, cioè cosa succede se UN< b , Quello B< а eseguita. Ma da queste uguaglianze, per il Teorema 12, abbiamo UN< а, il che è impossibile.

Poiché la relazione “minore di” che abbiamo definito è antisimmetrica, transitiva e possiede la proprietà di connessione, è una relazione di ordine lineare, e l’insieme dei numeri naturali insieme ordinato linearmente.

Dalla definizione di “minore” e dalle sue proprietà si possono dedurre le proprietà note dell'insieme dei numeri naturali.

Teorema 15. Di tutti i numeri naturali, uno è il numero più piccolo, cioè IO< а для любого натурального числа a¹1.

Prova. Permettere UN - qualsiasi numero naturale. Allora sono possibili due casi: un = 1 e un¹ 1. Se un = 1, allora esiste un numero naturale B, seguito da a: a \u003d b " \u003d b + io = 1+ B, cioè, per la definizione di "meno di", 1< UN. Pertanto, qualsiasi numero naturale è uguale a 1 o maggiore di 1. Oppure, uno è il numero naturale più piccolo.

La relazione "minore di" è connessa all'addizione e alla moltiplicazione dei numeri per le proprietà della monotonicità.

Teorema 16.

a = b => a + c = b + c e a c = b c;

UN< b =>a+c< b + с и ас < bс;

a > b => a + c > b + c e ac > bc.

Prova. 1) La validità di questa affermazione deriva dall'unicità dell'addizione e della moltiplicazione.

2) Se UN< b, allora c'è un numero naturale K, Che cosa UN + k = b.
Poi B+ c = (a + k) + c = a + (k + c) = a + (c+ A)= (a+c)+k. Uguaglianza B+ c = (a + c) + k significa che a+c< b + Con.

Allo stesso modo, è dimostrato UN< b =>asso< bс.

3) La dimostrazione è simile.

Teorema 17(converso al Teorema 16).

1) UN+ c = b + c O ac ~ bc-Þ un = b

2) a+c< Ь + с O asso< avanti CristoÞ UN< Ь:

3) a + c > b+ con o ac > acÞ a > b.

Prova. Dimostriamolo, ad esempio asso< bс Dovrebbe UN< b Supponiamo il contrario, cioè che la conclusione del teorema non regge. Allora non può essere un = b. perché allora l'uguaglianza varrebbe ac = ac(Teorema 16); non può essere UN> B, perché allora lo farebbe ac > ac(Teorema!6). Pertanto, secondo il Teorema 12, UN< b.

Dai Teoremi 16 e 17 si possono dedurre le ben note regole per l'addizione e la moltiplicazione termine per termine delle disuguaglianze. Li lasciamo cadere.

Teorema 18. Per qualsiasi numero naturale UN E B; esiste un numero naturale n tale che nb> a.

Prova. Per chiunque UN c'è un tale numero P, Che cosa n > a. Per fare questo, è sufficiente prendere n = un+ 1. Moltiplicare termine per termine le disuguaglianze P> UN E B> 1, otteniamo pb > UN.

Le proprietà considerate della relazione "minore di" implicano caratteristiche importanti dell'insieme dei numeri naturali, che presentiamo senza dimostrazione.

1. Non per nessun numero naturale UN non esiste un numero naturale del genere P, Che cosa UN< п < а + 1. Questa proprietà si chiama proprietà
discrezione insiemi di numeri naturali e i numeri UN E un+ 1 ha chiamato limitrofo.

2. Qualsiasi sottoinsieme non vuoto di numeri naturali contiene
il numero più piccolo.

3. Se M- sottoinsieme non vuoto dell'insieme dei numeri naturali
e c'è un numero B, quello per tutti i numeri x da M non eseguito
uguaglianza x< B, poi nella moltitudine Mè il numero più grande.

Illustriamo le proprietà 2 e 3 con un esempio. Permettere Mè un insieme di numeri a due cifre. Perché Mè un sottoinsieme di numeri naturali e per tutti i numeri di questo insieme la disuguaglianza x< 100, то в множестве Mè il numero più grande 99. Il numero più piccolo contenuto nell'insieme dato M, - numero 10.

Pertanto, la relazione “minore di” ha permesso di considerare (e in alcuni casi dimostrare) un numero significativo di proprietà dell’insieme dei numeri naturali. In particolare è ordinato linearmente, discreto, ha il numero più piccolo 1.

Con il rapporto "meno" ("maggiore") per i numeri naturali, gli studenti più giovani vengono conosciuti proprio all'inizio della formazione. E spesso, insieme alla sua interpretazione teorica degli insiemi, viene utilizzata implicitamente la definizione da noi data nel quadro della teoria assiomatica. Ad esempio, gli studenti possono spiegare che 9 > 7 perché 9 è 7+2. Uso frequente e implicito delle proprietà di monotonicità dell'addizione e della moltiplicazione. Ad esempio, i bambini spiegano che "6 + 2< 6 + 3, так как 2 < 3».

Esercizi

1 Perché l'insieme dei numeri naturali non può essere ordinato secondo la relazione "segue immediatamente"?

Formulare una definizione di relazione a > b e dimostrare che è transitiva e antisimmetrica.

3. Dimostrare che se a, b, c sono numeri naturali, allora:

UN) UN< b Þ ас < bс;

B) UN+ Con< b + su> UN< Ь.

4. Quali teoremi sulla monotonicità dell'addizione e della moltiplicazione possono
utilizzo da parte degli studenti più giovani durante il completamento del compito “Confronta senza eseguire calcoli”:

a) 27 + 8 ... 27 + 18;

b) 27-8...27-18.

5. Quali proprietà dell'insieme dei numeri naturali vengono implicitamente utilizzate dagli studenti più giovani quando eseguono i seguenti compiti:

A) Annota i numeri maggiori di 65 e minori di 75.

B) Nominare i numeri precedenti e successivi in relazione al numero 300 (800.609.999).

C) Qual è il numero di tre cifre più piccolo e più grande.

Sottrazione

Nella costruzione assiomatica della teoria dei numeri naturali, la sottrazione è solitamente definita come l'operazione inversa dell'addizione.

Definizione. La sottrazione dei numeri naturali aeb è un'operazione che soddisfa la condizione: a - b \u003d c se e solo se b + c \u003d a.

Numero un-b si chiama differenza tra i numeri a e B, numero UN- decrescente, numero B- sottraibile.

Teorema 19. Differenza dei numeri naturali UN- B esiste se e solo se B< а.

Prova. Lascia che la differenza UN- B esiste. Quindi, per definizione di differenza, esiste un numero naturale Con, Che cosa b + c = un, e questo significa questo B< а.

Se B< а, allora, per la definizione della relazione “minore di”, esiste un numero naturale c tale che b + c = a. Quindi, per la definizione di differenza, c \u003d a - b, quelli. differenza un-b esiste.

Teorema 20. Se la differenza dei numeri naturali UN E B esiste, allora è unico.

Prova. Supponiamo che ci siano due diversi valori della differenza tra i numeri UN E B;: un-b= c₁ E un-b= c₂, E c₁ ¹ c₂ . Quindi, per definizione di differenza, abbiamo: a = b + c₁, E a = b + c₂ : . Ne consegue quindi che B+ c₁ = b + c₂ : e sulla base del Teorema 17 concludiamo, c₁ = c₂.. Siamo arrivati a una contraddizione con l'ipotesi, il che significa che è falsa, e questo teorema è vero.

Sulla base della definizione della differenza dei numeri naturali e delle condizioni per la sua esistenza, è possibile comprovare le note regole per sottrarre un numero da una somma e una somma da un numero.

Teorema 21. Permettere UN. B E Con- numeri interi.

e se a > c, allora (a + b) - c = (a - c) + b.

b) Se b > c. quindi (a + b) - c - a + (b - c).

c) Se a > c e b > c. quindi puoi utilizzare una qualsiasi di queste formule.
Prova. Nel caso a) la differenza di numeri UN E C esiste perché a > c. Indichiamolo con x: a - c \u003d x. Dove a = c+x. Se (UN+ b) - c = y. allora, per la definizione della differenza, UN+ B = Con+ A. Sostituiamo invece in questa uguaglianza UN espressione c+x:(c + x) + b = c + y. Usiamo la proprietà di associatività dell'addizione: c + (x + b) = c+ A. Trasformiamo questa uguaglianza in base alla proprietà di monotonicità dell'addizione, otteniamo:

x+b = sì..Sostituendo x in questa equazione con l'espressione AC, avrà (UN - G) + b = y. Abbiamo quindi dimostrato che se a > c, allora (a + b) - c = (a - c) + b

La dimostrazione si svolge analogamente nel caso b).

Il teorema dimostrato può essere formulato come una regola facile da ricordare: per sottrarre un numero dalla somma, è sufficiente sottrarre questo numero da un termine della somma e aggiungere un altro termine al risultato ottenuto.

Teorema 22. Permettere a, b e c - numeri interi. Se a > b+ c, quindi UN- (b + c) = (a - b) - c O a - (b + c) \u003d (a - c) - b.

La dimostrazione di questa teoria è simile alla dimostrazione del Teorema 21.

Il Teorema 22 può essere formulato come regola, per sottrarre la somma dei numeri da un numero, è sufficiente sottrarre da questo numero successivamente ogni termine uno dopo l'altro.

Nell'educazione matematica elementare, la definizione di sottrazione come inverso dell'addizione di solito non viene data in forma generale, ma viene utilizzata costantemente, a partire dall'esecuzione di operazioni su numeri a una cifra. Gli studenti dovrebbero essere ben consapevoli che la sottrazione è correlata all'addizione e utilizzare questa relazione durante i calcoli. Sottraendo, ad esempio, il numero 16 dal numero 40, gli studenti ragionano come segue: “Sottrai il numero 16 da 40 - cosa significa trovare un numero che, sommato al numero 16, dà 40; questo numero sarà 24, poiché 24 + 16 = 40. Quindi. 40 - 16 = 24".

Le regole per sottrarre un numero da una somma e una somma da un numero nel corso elementare di matematica costituiscono la base teorica per vari metodi di calcolo. Ad esempio, il valore dell'espressione (40 + 16) - 10 può essere trovato non solo calcolando la somma tra parentesi, e quindi sottraendo da essa il numero 10, ma anche in questo modo;

a) (40 + 16) - 10 = (40 - 10) + 16 = 30 + 16 = 46:

b) (40 + 16) - 10 = 40 + (16- 10) = 40 + 6 = 46.

Esercizi

1. È vero che ogni numero naturale si ottiene da quello immediatamente successivo sottraendo uno?

2. Qual è la peculiarità della struttura logica del Teorema 19? Si può formulare con le parole “necessario e sufficiente”?

3. Dimostrare che:

e se b > c, Quello (a + b) - c \u003d a + (b - c);

b) se a > b + c, Quello un - (b+ c) = (a-b)-c.

4. È possibile, senza eseguire calcoli, dire quali espressioni saranno uguali:

a) (50 + 16) - 14; d) 50 + (16 -14 ),

b) (50 - 14) + 16; e) 50 - (16 - 14);
c) (50 - 14) - 16, f) (50 + 14) - 16.

a) 50 - (16 + 14); d) (50 - 14) + 16;

b) (50 - 16) + 14; e) (50 - 14) - 16;

c) (50 - 16) - 14; e) 50 - 16 - 14.

5. Quali proprietà della sottrazione sono la base teorica dei seguenti metodi di calcolo studiati nel corso iniziale di matematica:

12 - 2-3 12 -5 = 7

b) 16-7 \u003d 16-6 - P;

c) 48 - 30 \u003d (40 + 8) - 30 \u003d 40 + 8 \u003d 18;

d) 48 - 3 = (40 + 8) - 3 = 40 + 5 = 45.

6. Descrivere possibili modi per calcolare il valore di un'espressione della forma. un-b- Con e illustrarli con esempi concreti.

7. Dimostralo per B< а e qualsiasi c naturale l'uguaglianza (a - b) c \u003d ac - bc.

Istruzioni. La dimostrazione si basa sull’Assioma 4.

8. Determinare il valore dell'espressione senza eseguire calcoli scritti. Giustificare le risposte.

a) 7865 × 6 - 7865 × 5: b) 957 × 11 - 957; c) 12×36 - 7×36.

Divisione

Nella costruzione assiomatica della teoria dei numeri naturali, la divisione è solitamente definita come l'operazione inversa della moltiplicazione.

Definizione. La divisione dei numeri naturali a e b è un'operazione che soddisfa la condizione: a: b = c se e solo se, A quando b× c = a.

Numero a:b chiamato privato numeri UN E B, numero UN divisibile, numero B- divisore.

Come è noto, non sempre esiste la divisione sull'insieme dei numeri naturali, e non esiste un criterio così conveniente per l'esistenza di un quoziente come esiste per una differenza. Esiste solo una condizione necessaria per l'esistenza del particolare.

Teorema 23. Perché esista un quoziente di due numeri naturali UN E B, è necessario che B< а.

Prova. Sia il quoziente dei numeri naturali UN E B esiste, cioè esiste un numero naturale c tale che ac = a. Poiché per ogni numero naturale 1 la disuguaglianza 1 £ Con, quindi moltiplicando entrambe le sue parti per un numero naturale B, noi abbiamo B£ avanti Cristo. Ma bc \u003d a, quindi, B£ UN.

Teorema 24. Se il quoziente dei numeri naturali UN E B esiste, allora è unico.

La dimostrazione di questo teorema è simile alla dimostrazione del teorema sull'unicità della differenza dei numeri naturali.

Sulla base della definizione di numeri naturali parziali e delle condizioni per la sua esistenza, è possibile comprovare le note regole per dividere una somma (differenza, prodotto) per un numero.

Teorema 25. Se i numeri UN E B diviso per il numero Con, poi la loro somma a+bè divisibile per c, e il quoziente ottenuto dividendo la somma UN+ B per numero Con,è uguale alla somma dei quozienti ottenuti dividendo UN SU Con E B SU Con, cioè. (a+b):c \u003d a: c + b:Con.

Prova. Dal numero UN diviso per Con, allora esiste un numero naturale x = UN; con quello a = cx. Allo stesso modo, esiste un numero naturale y = b:Con, Che cosa

B= su. Ma allora a + b = cx+ su = - c(x + y). Significa che a+bè divisibile per c, e il quoziente ottenuto dividendo la somma UN+ B al numero c, equivale a x + sì, quelli. ascia + b: c.

Il teorema dimostrato può essere formulato come regola per dividere una somma per un numero: per dividere la somma per un numero è sufficiente dividere ogni termine per questo numero e sommare i risultati.

Teorema 26. Se numeri naturali UN E B diviso per il numero Con E a > b poi la differenza un-bè divisibile per c, e il quoziente ottenuto dividendo la differenza per il numero c è uguale alla differenza dei quozienti ottenuti dividendo UN SU Con E B a c, cioè (a - b):c \u003d a:c - b:c.

La dimostrazione di questo teorema si svolge in modo analogo alla dimostrazione del teorema precedente.

Questo teorema può essere formulato come regola per dividere una differenza per un numero: Per Per dividere la differenza per un numero è sufficiente dividere il minuendo e il sottraendo per questo numero e sottrarre il secondo dal primo quoziente.

Teorema 27. Se un numero naturale UNè divisibile per un numero naturale c, quindi per qualsiasi numero naturale B lavoro abè diviso in pag. In questo caso il quoziente ottenuto dividendo il prodotto ab al numero da , è uguale al prodotto del quoziente ottenuto dividendo UN SU Con, e numeri b: (a × b):c - (a:c) × b.

Prova. Perché UN diviso per Con, allora esiste un numero naturale x tale che COME= x, da cui a = cx. Moltiplicando entrambi i membri dell'equazione per B, noi abbiamo ab = (cx)b. Poiché la moltiplicazione è associativa, allora (cx)b = c(xb). Da qui (a b): c \u003d x b \u003d (a: c) b. Il teorema può essere formulato come regola per dividere un prodotto per un numero: per dividere un prodotto per un numero è sufficiente dividere uno dei fattori per questo numero e moltiplicare il risultato per il secondo fattore.

Nell'educazione matematica elementare, la definizione di divisione come operazione dell'inverso della moltiplicazione, di regola, non è data in forma generale, ma viene costantemente utilizzata, a partire dalle prime lezioni di familiarità con la divisione. Gli studenti dovrebbero essere ben consapevoli che la divisione è correlata alla moltiplicazione e utilizzare questa relazione nei calcoli. Dividendo, ad esempio, 48 per 16, gli studenti ragionano così: “Dividere 48 per 16 significa trovare un numero che, moltiplicato per 16, sarà 48; questo numero sarà 3, poiché 16 × 3 = 48. Pertanto, 48: 16 = 3.

Esercizi

1. Dimostrare che:

a) se il quoziente dei numeri naturali aeb esiste, allora è unico;

b) se numeri aeb sono divisi in Con E a > b Quello (a - b): c \u003d a: c - b: c.
2. È possibile affermare che ogni uguaglianza data è vera:
a) 48:(2×4) = 48:2:4; b) 56:(2×7) = 56:7:2;

c) 850:170 = 850:10:17.

Quale regola è una generalizzazione di questi casi? Formulatelo e dimostratelo.

3. Quali proprietà della divisione costituiscono la base teorica
svolgendo i seguenti compiti offerti agli studenti della scuola primaria:

è possibile, senza eseguire la divisione, dire quali espressioni avranno gli stessi valori:

a) (40+8): 2; c) 48:3; e) (20+28): 2;

b) (30+16):3; d)(21+27):3; f) 48:2;

Le uguaglianze sono vere:

a) 48:6:2 = 48:(6:2); b) 96:4:2 = 96:(4-2);

c) (40 - 28): 4 = 10-7?

4. Descrivere i possibili modi per calcolare il valore di un'espressione
tipo:

UN) (UN+ avanti Cristo; B) UN:B: Con; V) ( a×b): Con .

Illustrare i metodi proposti con esempi specifici.

5. Trovare i valori dell'espressione in modo razionale; loro
giustificare le azioni:

a) (7 × 63):7; c) (15 × 18):(5× 6);

b) (3 × 4× 5): 15; d) (12 × 21): 14.

6. Giustificare i seguenti metodi di divisione per un numero a due cifre:

a) 954:18 = (900 + 54): 18 = 900:18 + 54:18 = 50 + 3 = 53;

b) 882:18 = (900 - 18): 18 = 900:18 - 18:18 = 50 - 1 = 49;

c) 480:32 = 480: (8 × 4) = 480:8:4 = 60:4 = 15:

d) (560 × 32): 16 = 560(32:16) = 560×2 = 1120.

7. Senza dividere per un angolo, trova il più razionale
modo privato; giustificare il metodo scelto:

a) 495:15; c) 455:7; e) 275:55;

6) 425:85; d) 225:9; e) 455:65.

Lezione 34. Proprietà dell'insieme degli interi non negativi

1. L'insieme degli interi non negativi. Proprietà dell'insieme degli interi non negativi.

2. Il concetto di segmento della serie naturale dei numeri e il conteggio degli elementi di un insieme finito. Numeri naturali ordinali e quantitativi.

Esercizi

1.. Usando la definizione di moltiplicazione, trova i valori delle espressioni:
a) 3 3; 6) 3 4; c)43.

2. Annota la proprietà distributiva della moltiplicazione a sinistra rispetto all'addizione e dimostrala. Quali trasformazioni di espressioni sono possibili sulla sua base? Perché è diventato necessario considerare la distributività della moltiplicazione sinistra e destra rispetto all'addizione?

3. Dimostrare la proprietà di associatività della moltiplicazione dei numeri naturali. Quali trasformazioni di espressioni sono possibili sulla sua base? Questa proprietà viene insegnata alle scuole elementari?

4. Dimostrare la proprietà commutativa della moltiplicazione. Fornire esempi del suo utilizzo in un corso elementare di matematica.

5. Quali proprietà della moltiplicazione possono essere utilizzate per trovare il valore di un'espressione:

a) 5 (10+4); 6)125 15 6; c) (8 379) 125?

6. È noto che 37 3 = 111. Usando questa uguaglianza, calcola:

a) 37 18; 6)18512.

Giustificare tutte le trasformazioni.

7. Determinare il valore dell'espressione senza eseguire calcoli scritti. Giustifica la tua risposta:

a) 8962 8 + 8962 2; b) 63402 3 + 63402 97; c) 849 +849 9.

8 .. Quali proprietà di moltiplicazione utilizzeranno gli studenti della scuola primaria quando completano le seguenti attività:

È possibile, senza fare calcoli, dire quali espressioni avranno gli stessi valori:

a) 3 7 + 3 5; 6) 7 (5 + 3): c) (7 + 5) 3?

Le uguaglianze sono vere:

a) 18 5 2 = 18 (5 2); c) 5 6 + 5 7 = (6 + 7) 5;

b) (3 10) 17 = 3 10 17; d) 8 (7 + 9) = 8 7 + 9 8?
È possibile, senza eseguire calcoli, confrontare i valori delle espressioni:

a) 70 32 + 9 32 ... 79 30 + 79 2; 6) 87 70 + 87 8 ... 80 78 + 7 78?

Lezione 33 Sottrazione e divisione di interi non negativi

1. Ordinamento dell'insieme dei numeri naturali.

2. Definizione di sottrazione di numeri interi non negativi

3. Divisione di numeri interi non negativi. L'impossibilità di dividere per zero. Divisione con resto.

In queste condizioni si dice anche che il numero B Di più UN e scrivi b > a.

Teorema 12. Per qualsiasi numero naturale UN E B Si verifica una ed una sola delle seguenti tre relazioni: a = b, a > b, UN < B.

Omettiamo la dimostrazione di questo teorema.. Da questo teorema segue che se

un¹b, O UN< b, O a > b quelli. la relazione "minore di" ha la proprietà della connessione.

Teorema 13. Se UN< b E B< с. Quello UN< с.

Prova. Questo teorema esprime la proprietà di transitività della relazione “minore di”.

Teorema 14. Se UN< b, non è vero questo B< а. Prova. Questo teorema esprime la proprietà antisimmetria rapporto "meno".

Dimostriamolo prima per qualsiasi numero naturale UN non tu-!>! ■ )il suo atteggiamento UN< UN. Supponiamo il contrario, cioè Che cosa UN< а si verifica. Quindi, per la definizione della relazione "minore di", esiste tale numero naturale Con, Che cosa UN+ Con= UN, e questo contraddice il Teorema 6.

Dalla definizione di “minore” e dalle sue proprietà si possono dedurre le proprietà note dell'insieme dei numeri naturali.

Teorema 15. Di tutti i numeri naturali, uno è il numero più piccolo, cioè IO< а для любого натурального числа a¹1.

La relazione "minore di" è connessa all'addizione e alla moltiplicazione dei numeri per le proprietà della monotonicità.

totale:0
In contatto con 0
Google+ 0
OK 0
Facebook 0